Define an indicator random variable X_kl = I { h(k) = h(l) } such that key k ≠ key l . X_kl represents the possible values of a collision occurrence (i.e. key k and l both hashed to same slot in the array). Since simple uniform hashing is used, the probability of a key x that hashed to a location in a table is .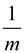

The probability that both keys h(k) and h(l) represent the same slot S (i.e. the probability for collision) is Pr { h(k) = h(l) }.

Pr { h(k) = h(l)} =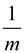

Therefore, the expectation value of both keys representing the same slot in the array is

E =

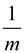
Now, the total expected number of collisions is E .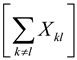

E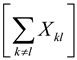 = E

Since, collisions are detected for combinations of key pairs (k , l) such that k ≠ l,

E =

=

=

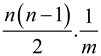
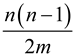
Hence, the expected number of collisions is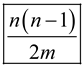

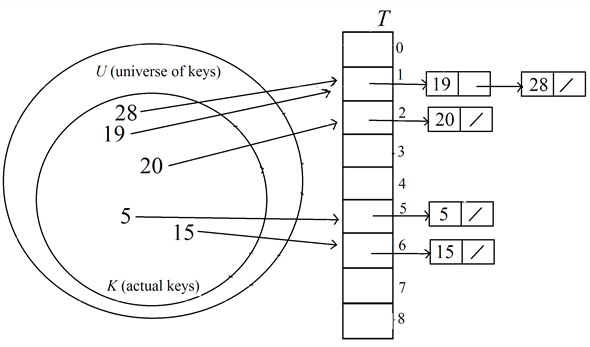
Inserting Keys into Hash Table with Collisions Resolved by Chaining

Chaining is one of the collision resolution techniques. In this technique, an index or slot 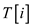of a hash table contains a linked list of elements with the same index 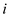which is calculated by the hash function.

The following procedure shows an implementation of a hash table such that each key 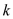of a universe 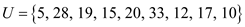maps to an index or slot in the hash table. Here, the number of slots in the table is 9. So the range of the index of the table is from 0 to 8. And the hash function is 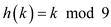. Therefore a slot 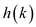is occupied by a value with key 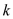. The hash table does not allow the duplicate values.

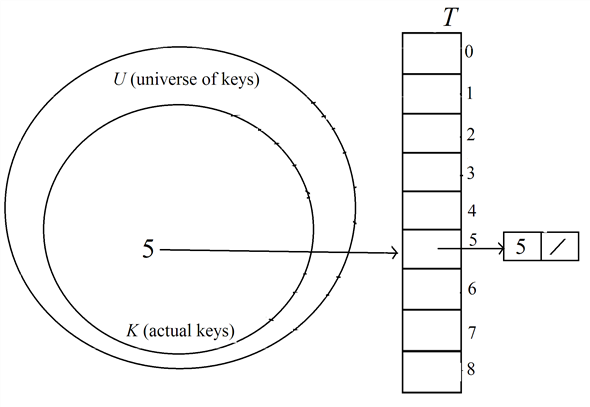
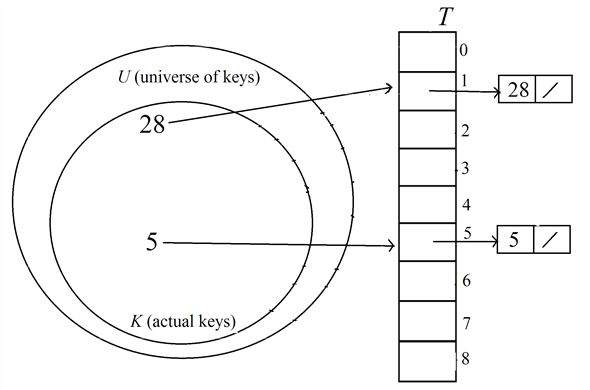
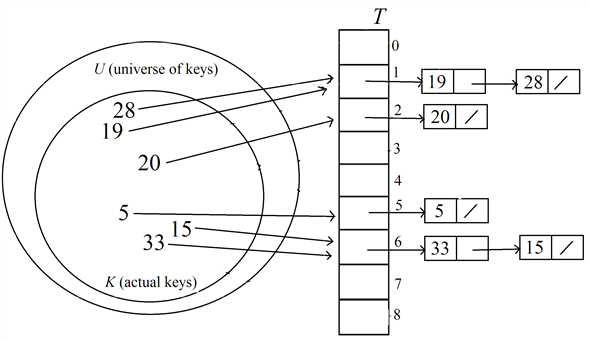
Insert the key 5 into the hash table :

Find the index of the table to insert the key 5 using the hash function,

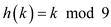
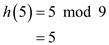
Therefore, the index to hold the key 5 is 5.

Search about the key 5 in the liked list of keys at the index 5 in the hash table.

Here, the key 5 is not found in the hash table.

Insert the key 5 as head of the list at the index 5 in the table.

After inserting the key 5, the hash table is as below.

Insert the key 28 into the hash table :

Find the index of the table to insert the key 28 using the hash function,

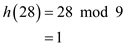
Therefore, the index to hold the key 28 is 1.

Search about the key 28 in the liked list of keys at the index 1 in the hash table.

Here, the key 28 is not found in the hash table.

Insert the key 28 as head of the list at the index 1 in the table.

After inserting the key 28, the hash table is as below.

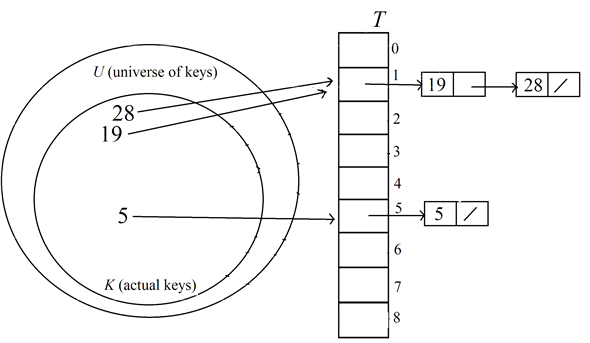
Insert the key 19 into the hash table :

Find the index of the table to insert the key 19 using the hash function,

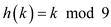
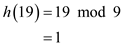
Therefore, the index to hold the key 19 is 1.

Search about the key 19 in the liked list of keys at the index 1 in the hash table.

Here, the key 19 is not found in the hash table.

Insert the key 19 as head of the list at the index 1 in the table.

After inserting the key 19, the hash table is as below.

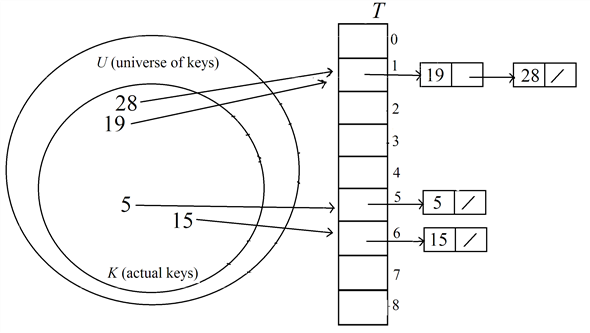
Insert the key 15 into the hash table :

Find the index of the table to insert the key 15 using the hash function,

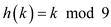
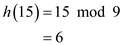
Therefore, the index to hold the key 15 is 6.

Search about the key 15 in the liked list of keys at the index 6 in the hash table.

Here, the key 15 is not found in the hash table.

Insert the key 15 as head of the list at the index 6 in the table.

After inserting the key 15, the hash table is as below.

Insert the key 20 into the hash table :

Find the index of the table to insert the key 20 using the hash function,

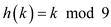
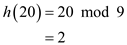
Therefore, the index to hold the key 20 is 2.

Search about the key 20 in the liked list of keys at the index 2 in the hash table.

Here, the key 20 is not found in the hash table.

Insert the key 20 as head of the list at the index 2 in the table.

After inserting the key 20, the hash table is as below.

Insert the key 33 into the hash table :

Find the index of the table to insert the key 33 using the hash function,

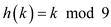
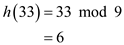
Therefore, the index to hold the key 33 is 6.

Search about the key 33 in the liked list of keys at the index 6 in the hash table.

Here, the key 33 is not found in the hash table.

Insert the key 33 as head of the list at the index 6 in the table.

After inserting the key 33, the hash table is as below.

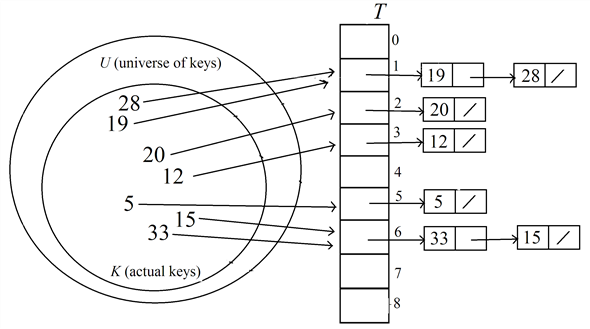
Insert the key 12 into the hash table :

Find the index of the table to insert the key 12 using the hash function,

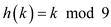
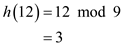
Therefore, the index to hold the key 12 is 3.

Search about the key 12 in the liked list of keys at the index 3 in the hash table.

Here, the key 12 is not found in the hash table.

Insert the key 12 as head of the list at the index 3 in the table.

After inserting the key 12, the hash table is as below.

Insert the key 17 into the hash table :

Find the index of the table to insert the key 17 using the hash function,

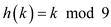
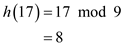
Therefore, the index to hold the key 17 is 8.

Search about the key 17 in the liked list of keys at the index 8 in the hash table.

Here, the key 17 is not found in the hash table.

Insert the key 17 as head of the list at the index 8 in the table.

After inserting the key 17, the hash table is as below.

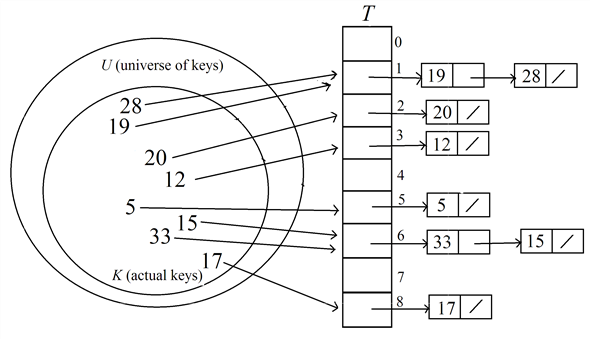
Insert the key 10 into the hash table :

Find the index of the table to insert the key 10 using the hash function,

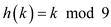
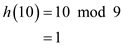
Therefore, the index to hold the key 10 is 1.

Search about the key 10 in the liked list of keys at the index 1 in the hash table.

Here, the key 10 is not found in the hash table.

Insert the key 10 as head of the list at the index 1 in the table.

After inserting the key 10, the hash table is as below.

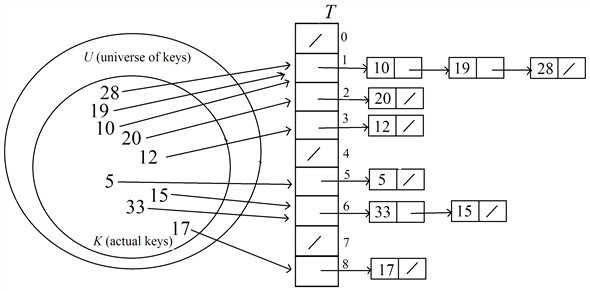
The slots with no elements are filled as NIL(/) in the resultant hash table .

When the hashing with chaining method is modified such that each list is maintained in sorting order, this modification effects the running time of successful searches, unsuccessful searches, insertions, and deletions as follows:

Running time effect on Successful search:

In changing scheme with unsorted lists, the complexity of successful search is 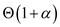where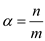. That is, time complexity of the successful search is proportional to the length of the list. In the worst case, the whole list is traversed to search an element. The length of the list is same, even though list is sorted or unsorted. Thus the modification does not affect the running time complexity of successful search.

Therefore, running time complexity of successful search, in chaining scheme with sorted lists, is still .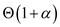

Running time effect on Unsuccessful search:

In chaining scheme with unsorted lists, the complexity of unsuccessful search is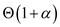. in the unsuccessful search, the running time of unsuccessful search is proportional to the length of the list. Thus, in chaining scheme with sorted list, the time complexity for unsuccessful search is also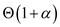. Hence, the modification also does not affect the running time of unsuccessful search.

Therefore, in chaining scheme with sorted list, running time complexity of unsuccessful search is still .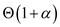

Running time effect on Deletion:

Before deleting an element from lists, it is required to find (or search) that element in list. That is, the running time for deletion is same as running time of searching time. Thus, the running time complexity of deletion is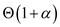. However, the case of deletion an element is similar to successful search. Therefore, the running time does not change with modified scheme.

Therefore, running time complexity of deletion in sorted list is still .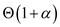

Running time effect on Insertion:

Since, in chaining scheme with unsorted lists, an element is inserted at the head of the list, the time complexity of insertion is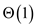. But, in the modified scheme, before inserting a new element, a proper place is required to be found (searched) in the sorted list. Running time for searching appropriate place is similar to running time for unsuccessful search. The running time complexity of unsuccessful search in chaining scheme with sorted lists is.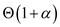

Thus, the running time complexity of insertion in modified scheme is .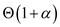

Since, the modified scheme does not affect the running time of successful search, un successful search and deletion, except the insertion, the modified scheme does not improve the performance chaining scheme. Moreover, it increases the running time of insertion.

A hash table with m slot size is denoted by T which is having the capacity to store n keys from the set universe U.

Since the table is having m slots, the hash function h maps the keys of universe U into the different slots of hash table.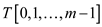

Proving that if keys are selected from U with 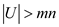, then there exist a subset of keys, having size n , in U such that all n keys hash to the same slot:

• Consider the universe U of size greater than nm (i.e.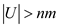) and a hash table T of size m.

• The set U contains the keys from 1, 2,…,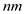,… and each key can be mapped to a slot into T.

• Since hashing with chaining is using, if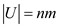, 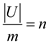keys can be mapped into each slot of T.

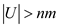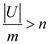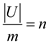• But, since, there exist some sub sets of size keys in U, such that all the keys of sub set can be mapped to same slot. Also there exist some sub sets of size keys in U, such that all the keys can be mapped to same slot.

• From the above, we can conclude that the set U has a set of size at least 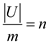, such that all the keys of the subset can be hash to same slot. That is, the number of keys mapped to same slot will be at least n.

• Since the searching time for a key is proportional to number of keys inserted into the slot, the worst case search time for hashing with chaining will be .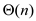

Hence if the n keys from the universe U with 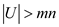, are inserted into a hash table T of size m , the minimum number of keys that can be mapped into same slot is n and thus the searching time for hashing with chaining will be .

Consider that n keys are hashed into a hash table of size m using chaining and the length of the each chain is known. Length of the longest chain is L.

To select a key uniformly at random means that each key in the hash table have equal probability to be selected.

The following procedure selects a key uniformly at random an returns in time O(L(1+m/n)).

• Repeat a loop until the procedure finds a non-empty bucket and return a key.

• Select a bucket b , randomly.(i.e. b= 0,1,…,m-1).

• The selected bucket may contain a chain of length between 0 to L.

• From the selected bucket b, randomly select a key k from the chain (i.e. k=1, 2, 3…L).

i)

The time required to retrieve an element and to return from a chain of length L =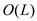

ii)

Expected number of elements per bucket is =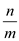

The probability for each element in the chain with length 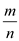to be selected =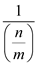

=

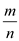
The probability for selecting and return any one of the elements in the chain with length =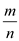

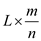
Therefore the time required to pick a key randomly is =

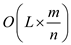
Hence, the total time taken by the procedure to select a key uniformly at random = +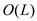

=

=

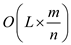
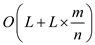
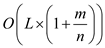
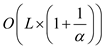= Since, ; .
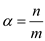
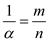