Longest-probe bound for hashing
Open addressing is the hashing technique in which for inserting an element in the table firstly we search for the elements if it is already contained in it, the search returns either the element or the free space in the array to fill that element.
In uniform hashing technique sequence of elements to be search
can be any of the m! permutation in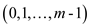 that is this
technique gives the method of searching which search in the full
list for the single element in the generalized way.
that is this
technique gives the method of searching which search in the full
list for the single element in the generalized way.
For the storage of n elements where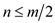 in a hash
table of capacity m items it uses the open addressing
technique.
in a hash
table of capacity m items it uses the open addressing
technique.
a . In the process of insertion of an element by using uniform hashing technique if the element is not found in the table then it is inserted into the first slot which do not contain any element.
If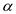 is the load
factor that is
is the load
factor that is 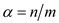 to search an
element which is not found in the table then the total expected
probes is maximum of
to search an
element which is not found in the table then the total expected
probes is maximum of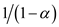 .
.
Assuming that a variable chosen represents
the probes which do not return the required variable then
represents
the probes which do not return the required variable then 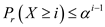 . We know
that
. We know
that 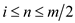 then
then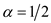 . The
probability of insertion of
. The
probability of insertion of 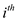 element in a
hash table that uses uniform hashing requires not less than
k probes so
element in a
hash table that uses uniform hashing requires not less than
k probes so 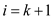 thus,
thus,
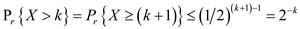
Hence 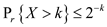
Thus for insertion of 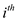 element in
the hash table by using uniform hashing where
element in
the hash table by using uniform hashing where 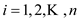 the
probability of storage is not more than
the
probability of storage is not more than when it
searches more than k times.
when it
searches more than k times.
b . For insertion of 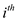 element in
the hash table by using uniform hashing where
element in
the hash table by using uniform hashing where 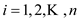 the
probability of storage is not more than
the
probability of storage is not more than when it
searches more than k times that is
when it
searches more than k times that is
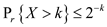
Here the probes required for the insertion of 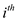 element in
hash table is more than
element in
hash table is more than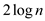 .
.
Thus, 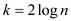 .
.
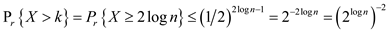
By using formulae of logarithm:

Thus
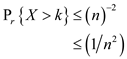
Hence the probability of storage for the insertion of 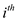 element is
element is
 for
for
 when it
probes
when it
probes 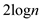 elements in
the table.
elements in
the table.
c. The insertion of 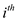 element in
the table requires
element in
the table requires  searches
and
searches
and  represents
the total number of searches necessary for the insertion of
n elements.
represents
the total number of searches necessary for the insertion of
n elements.
Consider an event A for which the number of probes
X are such that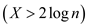 , and in
, and in
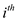 event
event
 the number of probes
the number of probes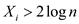 , for
, for
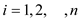 .
Then probability of events is as:
.
Then probability of events is as:

For n number of events according
to the Bool’s inequality:
according
to the Bool’s inequality:

Then for the set A of n events,

Hence if the insertion of 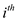 element in
the table requires
element in
the table requires  searches
and if
searches
and if 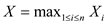 represents
the total number of searches necessary for the insertion of
n elements then:
represents
the total number of searches necessary for the insertion of
n elements then:
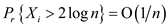
d . The expected length of the probe sequence for k probes is given by the formulae:
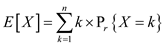
Breaking the sequence into two parts one from 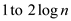 and the
other from
and the
other from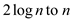 then,
then,

For the searching of 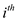 element for
which the number of probes less than
element for
which the number of probes less than 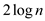 then
then
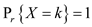 and for the
search when number of probes are greater than
and for the
search when number of probes are greater than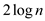 then
then
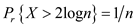 .
.
Thus,
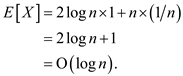
Hence, the expected total length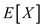 of the
maximum length probe succession is
of the
maximum length probe succession is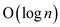 .
.
a.
The probability to hash a key to a specific slot is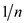 . Then the
probability to hash a particular set of k keys to a specific
slot and remaining keys to other slots is
. Then the
probability to hash a particular set of k keys to a specific
slot and remaining keys to other slots is  .
.
Here, k keys can be selected from n keys, in
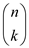 number of ways.
number of ways.
Thus, the probability to hash a set of k keys to a particular slot is as follows:

b.
Assume a random variable , which
denotes the number of keys hash to the slot
, which
denotes the number of keys hash to the slot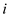 . And assume
that
. And assume
that  denotes an
event that the number of keys hashed to slot i is equal to
k(That is,
denotes an
event that the number of keys hashed to slot i is equal to
k(That is,  ). In part
(a), it is already proved that
). In part
(a), it is already proved that 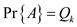 ,
,
Thus,
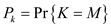 , where,
M is the maximum numbers of keys in any slot after all the
keys have been hashed.
, where,
M is the maximum numbers of keys in any slot after all the
keys have been hashed.
Now, put the values in the above expression:
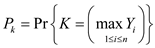
In other words,
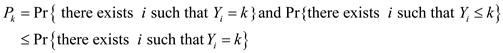
 (By Boole’s inequality)
(By Boole’s inequality)
Thus, 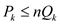 .
.
c.
To show the given in equality, first consider the following inferences:
• The probability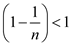 . Thus,
also
. Thus,
also .
.
• It is already known that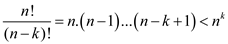 .
.
Thus, 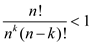
• From the Stirling’s approximation, 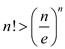 .
.
Consider the value of  :
:

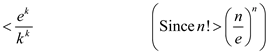
Therefore, 

d.
If  = 2, then
= 2, then
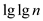 is
also 0. Therefore, assume
is
also 0. Therefore, assume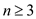 .
.
From part (c), it is proved that  for every
k. Thus, it is also true for k =
k0. That is,
for every
k. Thus, it is also true for k =
k0. That is,  .
.
Now, it is enough to prove that  or
or  .
.
After taking logarithms on both sides, the condition is as follows:

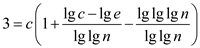
Suppose 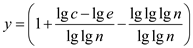 .
.
• Now, it is required to prove the existence of a constant
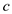 that is greater than 1 such that
that is greater than 1 such that 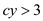 . It is
noting that
. It is
noting that  .
.
•
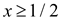 . Thus,
c > 6 works for
. Thus,
c > 6 works for 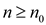 .
.
Thus, the value of n can be in the range 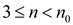 and for each
value of n in this range, a value for c can be
determined so that 3 < cx.
and for each
value of n in this range, a value for c can be
determined so that 3 < cx.
Therefore, it is proved that 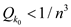
Now, it is remained to prove that  .
.
For k=k0, 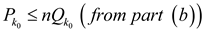

Here, To prove the given condition, choose a large value for
c such that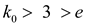 . Then
. Then
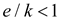 for all
for all  .
.
Thus, ek/kk decreases as k increases.
Therefore,  ,
where
,
where 
e.
The M ‘s expectation will be calculated as

Now, put the values in the above expression, then user will obtain;

Then use the above results, the user obtained:
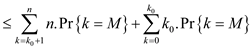
After putting the values, user will obtain the following:
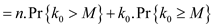
Since it is given that
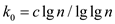 .
.
It is known that

and then,

Now, put the values in the above expression

Hence it is concluded that
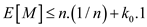
After putting the values:

This implies:
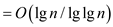
Therefore, 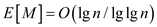 .
.
Quadratic probing
Quadratic probing or quadratic hashing is the hashing technique which reduces the collision in the table and it can be given by the following formulae,
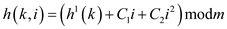
Where 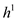 is any hash
function,
is any hash
function, are the
constants and
are the
constants and 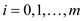 is bucket
size, k is the key to be inserted.
is bucket
size, k is the key to be inserted.
To prove that the scheme of hashing problem is an instance of
quadratic probing a numerical example is taken as consider
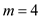 and
and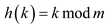 .
.
The numbers 29, 21, 13, 37 are the keys which we already inserted in the table for the schema now we will search for number 37 in the table below:
|
13 |
3 |
|
21 |
2 |
|
29 |
1 |
|
37 |
0 |
Firstly searching a number 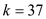 in the above
table by using the scheme of searching by taking
in the above
table by using the scheme of searching by taking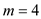 .
.
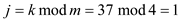 and
and
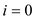
But at position 1 the value 29 is there so increase the value of i for next step
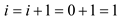
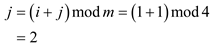
but at position2 the value 21 is there in the table so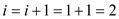
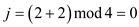
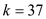 is found
hence the search complete.
is found
hence the search complete.Now searching the same value 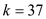 by using
general Quadratic probing formulae:
by using
general Quadratic probing formulae:

Assuming the value and
and
 and put these in quadratic formula as:
and put these in quadratic formula as:

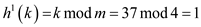
searching for 37
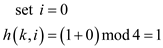
at position1 the value 37 is not found so increase i by 1
that is 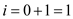 .
.
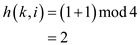
at position 2 the key 37 is not found so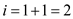 .
.
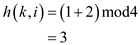
at position 3 the key 37 is not found so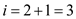 .
.
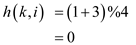
at position 0 the key 37 is found.
Hence for constants  and
and  of
“Quadratic probing” it shows the behavior same as the hashing
scheme.
of
“Quadratic probing” it shows the behavior same as the hashing
scheme.
b. Proving that for searching any key k in the table by using the search scheme it searches each position of the table if the key is not present in the table.
In the worst case that is when the key is not present in the table we search for each and every element of the table to match each key of table with the element to search.
The given algorithm searches each and every bucket of the table if the given key is not present in the table
Example: Search for 4 in the above hash table.
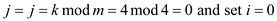
but at position 0, the value 29 is there so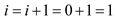
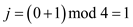
but at position1 the key 21 is there so for next iteration
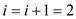
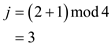
at position 3, the key 13 is present.
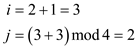
at position 0 the value 37 is found.
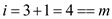
So element 4 is not present and we terminate search. We have searched each position of table.
Hence in the worst case that is if key is not present in the table or present in the reverse order then the search scheme probes in each position of the table.
Hashing and authentication
In a class of hash functions H each hash function
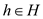 maps a
universe U which has keys to the value set
maps a
universe U which has keys to the value set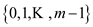 .
.
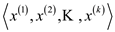 of k
keys that are distinct and for any hash function h chosen
randomly from the set the succession
of k
keys that are distinct and for any hash function h chosen
randomly from the set the succession can be one
from
can be one
from  sequences
which have length k with
sequences
which have length k with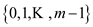 .
.a . If the hash family H is 2-universal
then each of its hash functions contain two keys so for the
keys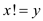 in a hash
function h, the sequence
in a hash
function h, the sequence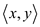 can be any
of sequence in the set
can be any
of sequence in the set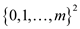 .
.
Therefore, as the hash function h changes within the set
of hash functions H, the count of collisions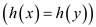 is
is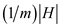 , and
H is universal.
, and
H is universal.
Hence if has set 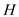 is
2-universal then this class H is universal class too.
is
2-universal then this class H is universal class too.
b . The universe U is a class of
n-tuples of the values that are taken from a set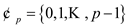 here
p is prime number. If an element
here
p is prime number. If an element , for any of
n-tuple
, for any of
n-tuple  the hash
function
the hash
function 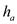 is
represented as:
is
represented as:

Proving that 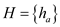 is universal
set but this universal set is not 2-universal.
is universal
set but this universal set is not 2-universal.
Assuming that a hash function h is selected from the hash
family H with the key 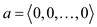 and b at
random that is without any prior information. Then for the
succession
and b at
random that is without any prior information. Then for the
succession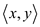 hash
function
hash
function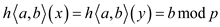 will never
be the sequence from the set
will never
be the sequence from the set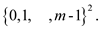
Hence H will not be a 2-universal class.
c . If the class of hash functions H is
changed as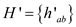 for the
keys
for the
keys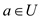 and
and
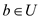 the hash function:
the hash function:

Proving that H’ is 2-universal class.
For a 2-universal hash class it is must that for each key
pair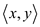 when
when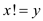 in a hash function the values
in a hash function the values 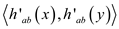 have equal
probability to occur when hash function is selected at random from
hash class H. For the changes in the hash function this is
proved as:
have equal
probability to occur when hash function is selected at random from
hash class H. For the changes in the hash function this is
proved as:
If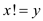 , we must
have
, we must
have  for some
i. Assume
for some
i. Assume 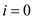 without any
loss in precision or generality. We define
without any
loss in precision or generality. We define
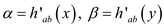 and
and
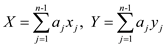 .The
equations for
.The
equations for 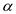 and
and
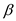 are
are 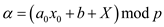 and
and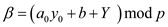 It
is clear that
It
is clear that 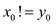 and p
is prime, so the solution for the equations of
and p
is prime, so the solution for the equations of 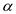 and
and
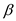 will be unique for
will be unique for  and
b.
and
b.
Consider that for the generation of all pairs of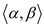 we must
control over the
we must
control over the 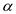 and
and
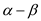 without
any dependency. We have
without
any dependency. We have

So
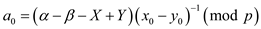
The expression is existing
and it not repeating because
is existing
and it not repeating because and the
value of p is prime. So
and the
value of p is prime. So 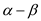 can be made
according to the need by selecting a
can be made
according to the need by selecting a  according to
condition. If we do so then we can also make
according to
condition. If we do so then we can also make 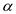 according
to our need by taking b as required.
according
to our need by taking b as required.
This puts a unique value of offset to 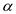 and
and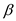 ,
by ignoring the difference
,
by ignoring the difference 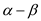 mod p
as it is. So, for
mod p
as it is. So, for , there is a
hash function
, there is a
hash function that
produces the values for
that
produces the values for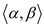 by selecting
the correct values of
by selecting
the correct values of  and
b.
and
b.
We know that there are 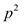 choices
possible for
choices
possible for and
b, and this is also true for
and
b, and this is also true for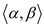 , and
each
, and
each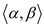 is produced
by taking only a single value of
is produced
by taking only a single value of  and
b. This is right for each
and
b. This is right for each  selections
of
selections
of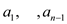 .
.
Hence, there are only functions
functions
 which is
used to produce the value pairs
which is
used to produce the value pairs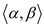 and
all
and
all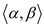 have equal
probability of being selected when
have equal
probability of being selected when  is selected
at random, so hash family H is 2-universal.
is selected
at random, so hash family H is 2-universal.
d . Assuming that Alice and Bob agreed on a hash
function 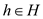 such that
every hash function maps the set of keys U to the values in
the set
such that
every hash function maps the set of keys U to the values in
the set here
p is prime value.
here
p is prime value.
After some time Alice has sent a message 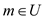 to Bob over
internet with the certification that
to Bob over
internet with the certification that 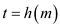 and Bob has
got the message in the form of
and Bob has
got the message in the form of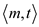 feels
satisfied by seeing tag t.
feels
satisfied by seeing tag t.
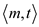 with
with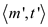 .
Then argue that the probability of receiving the messages
with
.
Then argue that the probability of receiving the messages
with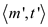 is
is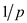 , without
any effect of number of opponent and computing power of
internet.
, without
any effect of number of opponent and computing power of
internet.In the hash class for a set of keys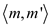 , all the
hash value sets
, all the
hash value sets 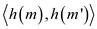 are selected
with same likeliness when the hash function h is selected at
random. In this case H will be 2-universal so all p
pairs
are selected
with same likeliness when the hash function h is selected at
random. In this case H will be 2-universal so all p
pairs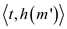 in the hash
class are equally probable.
in the hash
class are equally probable.
Hence if the opponent knows hash class H, then
seeing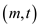 tells him
almost everything about
tells him
almost everything about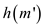 . Since for
all the p cases the probability is equal and so the sum of
this probability must be 1, for all
. Since for
all the p cases the probability is equal and so the sum of
this probability must be 1, for all 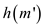 have
probability
have
probability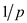 and the
opponent can do nothing but to guess.
and the
opponent can do nothing but to guess.