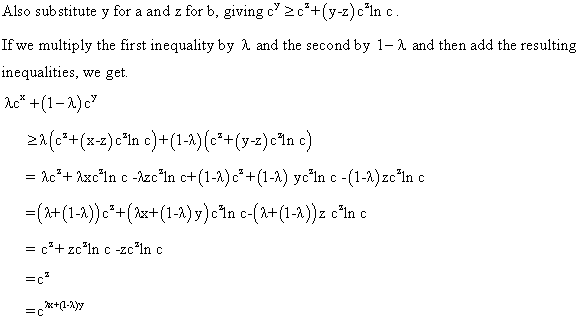Prove the equation 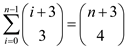 ……(1)
……(1)
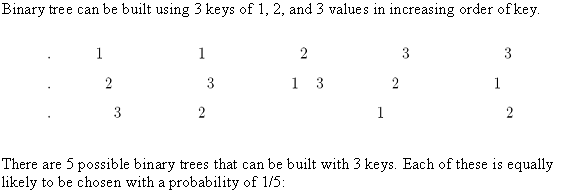
Equation can be proved using the following combination identities:
i)
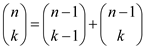 [Refer C-1-7]
[Refer C-1-7]
ii)
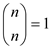
Hence,
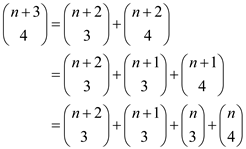
This can be extended up to 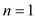 as:
as:

[Since, 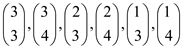 are not
valid]
are not
valid]
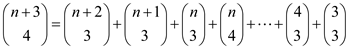 …… (2)
…… (2)
[Since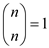 ,
, 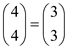 ]
]
Equation (2) can be expressed as follows:
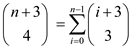
Therefore, 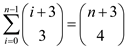
RANDOMIZED QUICKSORT
Randomization is a technique to improve the performance of the worst-case estimation of Quick sort. In a randomized algorithm, some random choice is made during the execution. As through the analysis, we find that running time of normal deterministic algorithm depends only on the input, but running time of randomized algorithm depends not only on the input, but also on the choices we make randomly on the algorithm. For a given set of input, running time of the randomized algorithm is not fixed. There are both, the best-case and the worst-case running time for a randomized algorithm. But for which input it is achieved, is not known; it can be any set of input.To understand the randomized Quick sort, we should have a better understanding of randomized partition.
Randomized partition (A, p, q),
Which works on, A
1. r= random (p, q) (that is to pick an integer uniformly between p and q at random)
And exchange a with
a
with
a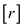 .
.
2. return partition (A, p, q).
So in this, we are picking an element randomly in the sequence and using it as a pivot to partition.
Randomized Quicksort (A, p, q),
Which used to, sort 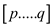
1. if p
2. S=randomized partition (A, p,
q)
3. Randomized Quicksort (A, p, s-1)
4. Randomized Quicksort (A, s+1,q)
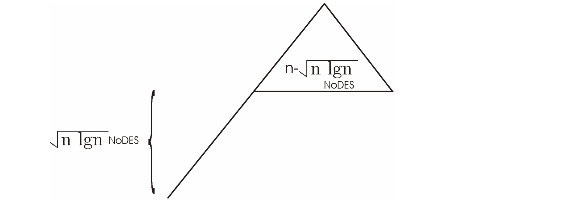
Here we are considering Randomized Quick sort on a
sequence of n distinct input numbers. For any k>0,
and having the permutation of n!, we have the running time
of 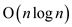 . So, we
choose the pivot, and perform
. So, we
choose the pivot, and perform 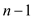 comparisons
(that is making comparison with all other elements with it) in the
process of splitting the array into a LESS of size 0 and a greater
of size
comparisons
(that is making comparison with all other elements with it) in the
process of splitting the array into a LESS of size 0 and a greater
of size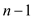 , or into a
LESS of size 1 and a GREATER of size
, or into a
LESS of size 1 and a GREATER of size  and further
to a less of size
and further
to a less of size 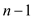 and a
greater of size 0; all these have an equal probability of
1/n each. So, the recurrence relation for the expected
number of comparisons T(n) is as follows:
and a
greater of size 0; all these have an equal probability of
1/n each. So, the recurrence relation for the expected
number of comparisons T(n) is as follows:
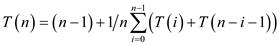
It can be rewritten by regrouping as:

And now this recurrence relation can be solved by a method of induction and guessing.
Generally pivot is used to split an array “roughly” in the
middle, which makes a guess of the form 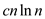 for some
constant value of c. Once the guess is made, we need to
evaluate the resultant summation. We can do it easily by making
upper bound, the sum by an integral. If the function
f(x) is an increasing function then,
for some
constant value of c. Once the guess is made, we need to
evaluate the resultant summation. We can do it easily by making
upper bound, the sum by an integral. If the function
f(x) is an increasing function then,

which can be easily seen by drawing a graph of f; and we know that an integral represents “the area under the curve”. In the case we use the fact that,
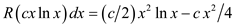
Now, by analysis, we guess that
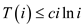 for
for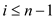 .
.
This works for the base case 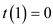 (that is if
there is only one element, then there is no comparison). By
induction, we have:
(that is if
there is only one element, then there is no comparison). By
induction, we have:

For c=2
So, for the n! Permutations, we have the running time
of 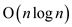 .
.