Consider the following pseudocode for Left-Rotation to interval tree.
In the following pseudocode MAX procedure is used to update the max attribute.
In left rotation first check the right child of node x and perform the left rotation according to the property of tree.
LEFT-ROTATE (T, x)
//store the right child of node x into variable y
1 y
right
[x]
//store the left child of y into right child of x
2 right[x]left[y]
//check if left child of x is not null
3 if left[x]!=NILL[T]
//add x as a parent node of left of y
4 p[left[y]]x
//copy parent of x into parent of y
5 P[y]p[x]
//if parent of x is null
6 if p[x]= NILL[T]
//copy the node y into root of tree.
7 root[T]y
//else if is used to check the left of parent of x
8 else if x=left[p[x]]
//copy y into left of parent of x
9 left[p[x]]y
//max function is used to update the max field of node x
10 Max[x] = MAX (max [int[x]], max [left[x]], max [right[x]])
11 else
//copy the node y in right of parent of x
12 right[p[x]]y
//copy the node x into left of y
13 Left[y] x
// max function is used to update the max field of node y.
14 Max[y] = MAX (max [int[y]], max [left[y]], max [right[y]])
In the above code no loop is used, the value of max attribute
gets updated by calling the function MAX. The MAX function requires
time complexity of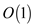 
.
All the remaining statements take time complexity of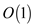
Therefore, the time complexity of above pseudocode is
order of 1 so the time complexity of LEFT-ROTATION is
.
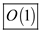Consider the following algorithm of interval search tree when all intervals are open.
INTERVAL-SEARCH (T, i)
//store the root of red- black tree into variable x
1 x= root [T]
//while loop is used to check tree is not null and node of tree does not overlap the //interval i
2 while x!= NILL [T] and i does not overlap int [x]
//if statement is used to check the left node of tree and maximum of left sub tree is
//greater than the lower point of interval.
3 if left[x]! = NILL [T] and max [left[x]]> i. low
//store left of x in variable x
4 x= left [x]
5 else
//store right of x in variable x
6 x= right[x]
7 return x
Explanation of algorithm:
• In open interval search tree there is no low endpoint and high endpoint.
• Change only in line three of the INTERVAL-SEARCH tree algorithm provided in the text book when all intervals are open.
• In line 3rd of algorithm, if statement is used to check the maximum endpoint in left sub tree of root node x which is always greater than the i. low.
• The left sub tree of root node x never overlap the low endpoint of interval which user wants to search because max [left[x]]> i. low.
In line 1 st of algorithm assignment
operator is used so the time complexity will be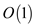 
and
in line 2 nd of the algorithm while loop is used
to traverse the each node of tree. Since the height of tree is
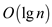so
the total time complexity of algorithm will be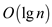
.
In the INTERVAL-SEARCH procedure, it is checked whether the current node, y overlaps the interval i or not. The explanation of the procedure is as follows:
• If the overlap does not exist, traverse either to the left child or the right child.
• MIN-LOW-ENDPOINT: Return the overlapping interval with the minimum low end point, if the current node y overlaps the interval i, and when some nodes in the right subtree overlap i, but no node in the left subtree overlaps i because, the keys are the low-end-points.
• If the current node, y is checked before the left subtree and if there is an interval that overlaps i in the left subtree of the node y, then it might return an interval whose low-end-point is not the minimum of the nodes overlapping i.
• Therefore, create the left subtree first.
• Check the right subtree in the same manner as in the INTERVAL-SEARCH that is, the left subtree cannot contain an interval that overlaps i, and the node, y does not overlap i.
Use an auxillary recursive algorithm MIN-INTERVAL-SEARCH-AUX (T, y, i) which returns an interval overlapping i with the minimum low endpoint or T.nil, if no such interval exists.
ALGORITHM: The algorithm is as follows:
MIN-INTERVAL-SEARCH (T, i)
return MIN-INTERVAL-SEARCH-AUX (T, y, i)
MIN-INTERVAL-SEARCH-AUX(T, y, i)
1 if y.left
T.nil and
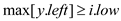
2 x=MIN-INTERVAL-SEARCH-AUX (T, y left, i)
3 if xT.nil
4 return x
5 else if i overlaps y
6 return y
7 else return T.nil
8 else if i overlap y
9 return y
10 else return MIN-INTERVAL-SEARCH-AUX (T, y.right, i)
Height of the tree: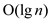 
Time complexity of MIN-INTERVAL-SEARCH (T, i):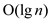
Interval Tree
Interval tree is an augmented data structure which, in very essence of it, is a binary tree. Every node has two kids and the values in the left kids are always less than the parent and in the right kid the values are greater than the root.
The difference is that in an interval tree the intervals are kept in the nodes rather than the single values.
An extended definition of the interval tree is as follows.
Interval tree is a red black tree used to maintain a dynamic set of elements, in which each element x contains an interval x.int.
Intervals are used for representation of various events that occupy continuous period of time.
Intervals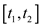 
are
represented as an object i,
Where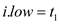 
represents
the low endpoint and
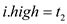represents the high endpoint.
Two interval i and i’ overlap,
if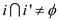
That is,
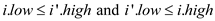
Two interval i and i’ satisfies the interval trichotomy,
If one of the properties hold exactly
1. i and i’ overlap.
2. i is to the left of i’ (that is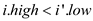
).
3. i is to the right of i’ (that is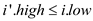
).
It supports different operations:
1. Interval-insert.
2. Interval-delete.
3. Interval-search.
Left traversing:
In order to check the overlapping intervals in the left child; if the left child is not t.nil and the low endpoint of the search intervals is less than the left_child.max then there could be overlaps in the left child.
Right traversing:
In order to check overlapping intervals in the right child; if the search interval does not overlap the left child then there could be overlaps in the right child.If there is interval overlap with the search node, then during the searching; delete that interval node from the tree, and continue the searching from the tree.
ALGORITHM FOR INTERVAL SEARCH
INTERVAL_SEARCH (T, i)
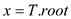
while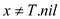 
and i
does not overlap x.int
do
if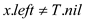 
and
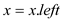
else
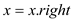
return
ALGORITHM FOR INTERVAL OVERLAPPING:
INTERVAL-OVERLAP-LIST (T, x, i)
if i overlaps x.int print x if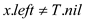and
INTERVAL-OVERLAP-LIST(T, x.left, i)
if 
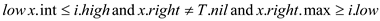INTERVAL-OVERLAP-LIST(T, x.right, i)
return xRunning time of the algorithm:
The running time of the algorithm can be calculated as below:
Have a look at the procedure for searching for the overlapping
interval. For the first overlapping interval to occur it might take
up-to the end of the list. This makes the worst possibility for the
search to be successful equal to
.
The tree has a total of k intervals. When the procedure
runs, every recursive call would access the next interval. The
runtime for this would remain the same as this is for binary tree.
When the same implication is applied to an interval tree, the cost
of execution for the code and search for value within the interval
would be added to the complexity making it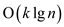
.
So when the overlapping is to be checked, the possibility to find an overlapping would be equal to the minimum possibility of the successful search for an overlapping.
So, this would be equal to
.
Interval Tree:
The color of the node in interval tree is same as red black
tree, parent and children node do not have same color. In interval
tree a node contain ordered pair of real integer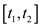 
where
.
The interval stored in the tree is represented with the help of
object. Suppose k is an object which represent the
interval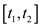, where
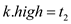and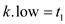
.
Consider the following modified INTERVAL-SEARCH() algorithm to find exactly interval i in tree T, the modification is highlighted with grey color.
INTERVAL-SEARCH-EXACTLY (T, i)
1. 
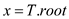
2. while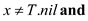 
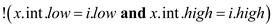
3. if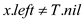 
and
4. 
5. else
6. 
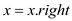
7. if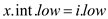 
and
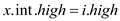
8. return x
9. else
10. return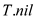 
Explanation:
• At first store the reference of root node in x.
• Implement a while loop to determine the interval in the tree. A loop continue iterate interval is not found or tree is not get completely traversed.
• In each iteration check left child exist or not and left child of current node is greater than low of i.
• After the termination of loop, if current node (x)
interval is same as interval of i then return the
pointer to that node otherwise return .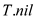
Time Complexity:
• The above INTERVAL-SEARCH-EXACTLY algorithm has one while
loop. Each iteration, of ‘while’ loop takes 
time.
• The height of n node tree is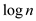
, in worst
case the number of iteration in above algorithm is equal to height
of tree.
Therefore the running time required by above algorithm is
.
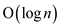MIN-GAP operation
Consider a dynamic set that is a set which does not have fixed elements that set support the MIN-GAP operation on set elements. MIN-GAP is the operation which returns the difference between a pair of closest elements of the set. Red Black Tree is a special type of tree in which each node is colored with either using red color or by black color that is all nodes contain an extra bit for the storage of the color of that node.
For implementing the dynamic set, that can support the MIN-GAP
operation on its elements, use the Red Black tree in which the
number of dynamic sets are implemented as the keys of nodes. The
searching for a key is a simple operation, as the TREE-SEARCH runs
in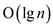 
time in the
red black tree; and will be like this after augmenting.
To insert a new node to the augmented tree with min-gap operation, it must contain some more information with each node in the tree. That is, the red-black tree is increased by the subsequent fields in every node.
1. The variable min-gap [NODE] contains the minimum gap
within the subtree unmoving at the Node. If Node may be a leaf that
is its youngsters are all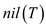 
,
then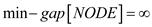
.
2. A variable min-value [NODE] contains the key with minimum worth within the subtree at NODE.
3. The variable max-value [NODE] contains the most worth (key) within the subtree at NODE.
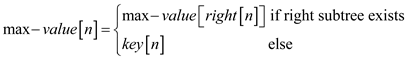
All the three variables must be associated with each and every
node of the tree, and when a node is inserted or deleted from the
tree, this information must be maintained with each node. That is,
the new variable will be maintained throughout insertion and
deletion, while not moving the 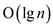period of
time.
The rationale for outlining the min-value and maximum
value is to make it double to calculate the minimum gap from info
at the node and its youngsters. MINIMUM GAP of the node merely
returns the MINIMM GAP held on at the tree root. Thus, it takes
the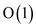
time to
return the min-gap of any node in the tree.
Consider the following assumptions to define the algorithm whose
time is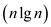
:
Define two sets L and R.
L represents the set of the left coordinates of the rectangle and R represents the set of the right coordinates of the rectangle.
• Now, sort both the sets in such a way that it will take
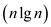time.
• Consider two pointers. One points to the set L and the other point to the set R.
• If the pointer that points to L is small, then call the interval search on T for the interval which is in the form of up-down and correspond to the left-hand side.
• If it consists of something that will intersect the bounds which are of up-down, then there is an intersection, therefore, stop.
• Otherwise, add the above intersection to T and increment the pointer that points to L.
• If the pointer points to R is the one which is small, then remove the interval which is up-down and correspond to the right-hand side and increase the pointer that points to R.
Since, the operations performed by the interval tree take the
time of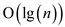
, and this
will call for at-most 3n times.
Hence, the runtime will be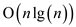 
.