a)

Two intervals are said to overlap if their intersection is non-empty. Since the intervals are closed intervals, the intersection of two or more intervals contains one of the maximum values of two intervals. Consider that a point of maximum overlap in a set is a point that overlaps the largest number of intervals in the set.

• Assume that there is no point of maximum overlap that is the endpoint of one of the segment.

• Consider that the overlap point p is in the internal point of n segments. So the point p must be the common point in all the segments.

• Now calculate the intersection of n segments, and then the points in the intersection are the common points of n segments. These points overlap all the n segments. Since, the intervals are closed one of these common points 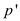must be an end point of one of the n segments.

• Consider only two segments, 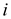and such that and

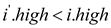
• Now, calculate intersection of two segments, then the intersection contains only one point 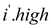, which is the point of maximum overlap.

Therefore there will be at least a point of maximum overlap that is an endpoint of one of the segments.

b)

Consider an RB-tree (Red-Black) created by all the endpoints we tend to insert endpoints one by one as a sweep line scanning from left to right.

With every left end e, associate a price 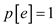(overlap increased by 1) and

With every right end e associate a price 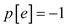(overlap decreased by 1).

Once multiple endpoints have an equivalent price, insert all the left endpoints there upon price before inserting any of the proper endpoints there upon price. For the perception consider that are the linearly sorted end points.

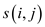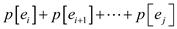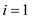Consider denote the additionso forto 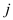we have to search such i for which 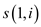is greatest. The nodes in the tree contains three variables with them we tend to store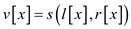, the addition of the values of all successive sibling nodes in x’s subtree.

Now, jointly store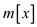, the uppermost price calculated from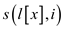for any i and we store 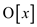because the price of i that 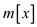achieves its most.

For the picket, we tend to outline.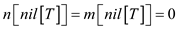

We can cipher these attributes from bottom to top in a linear procedure therefore

,

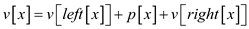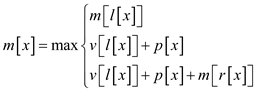
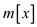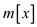From the above formulae ofonce we tend to perceive the way to cipher, it is simple to cipher 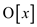from the data in x and its children. Come back the interval whose end is portrayed by.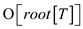

In the definition of new attributes for the tree every operation that is INTERVAL-INSERT and INTERVAL-DELETE runs intime. In the process of finding the maximum overlap point from the tree it just returns the value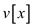which is already stored with each node so FIND-POM operation takes only time.

Josephus permutation:

The circular list is the linked list in which the last contains the address of the first node.

This list is used in the application to find something in a loop format again and again. Order statics tree is the form of tree which is created by adding some more values in the BST (Binary Search Tree). This is also called augmented tree structure and it supports some operations as choosing minimum element and rank of any node in the tree.

a.

Creating a circular list of the n numbers, in which every node has 2 fields, v which denotes the amount and next pointer. The values 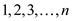are inserted to the list in the same order which takestime. This is the circular list so the 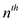node contains the address of 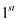node.

Now, starting the scan of list from first node and output each 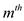component and delete it from list until the list is empty. This method takes 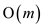time per component, for a complete time of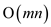. Since m could be a constant, we have a tendency to get 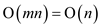time.

b. Use an order-statistic tree T, and call the procedures NODE-INSERT,NODE-DELETE, NODE-RANK, and NODE-SELECT. The algorithm for JOSEPHUS is as given below in which first we initialize a tree T and creating the nodes that contains the values from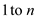in each successive node and then add these nodes into the tree.

Now, scanning the tree from last node to first node and select the appropriate node x from the tree and print its value.

JOSEPHUS (n, m)

1. initialize T to be empty tree

2. for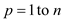

// creates a new node x

3. create a node x with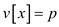

// inserts a node x in the tree T

4.

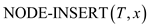
5.

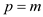
6. fo r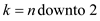

7.

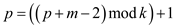
// stores the selected node p into the variable x from the tree T

8.

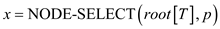
9. print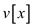

// DELETES the node x from the tree T

10. NODE-DELETE(T,x)

The above algorithm takes 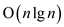time to make up the order-statistic tree T, so we tend to create calls (line number 2 of the above algorithm) to the order-statistic tree procedures, every of that takes (line number 6 of the above algorithm time.

Thus, the whole time taken by the algorithm is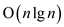.