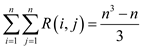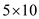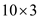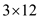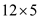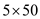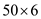This can be done by computing MATRIX – CHAIN – ORDER(P) where
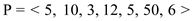or
simply using the equation
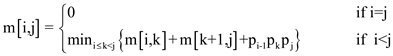
p0=5, p1=10, p2=3, p3=12, p4=5, p5=50, p6=6
m[1,1] = 0
m[2,2] = 0
m[3,3] = 0
m[4,4] = 0
m[5,5] = 0
m[6,6] = 0
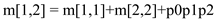
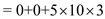
= 150
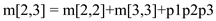
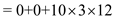
= 360
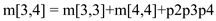
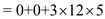
= 180
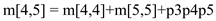
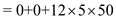
= 3000
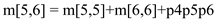
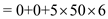
= 1500
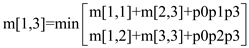
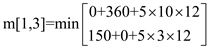
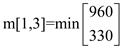
m[1,3] = 330
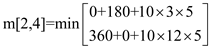
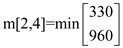
m[2,4] = 330
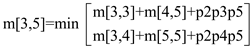
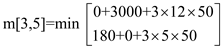
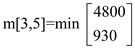
m[3,5] = 930
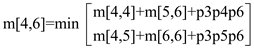
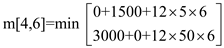
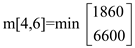
m[4,6] = 1860
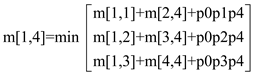
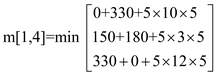
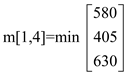
m[1,4] = 405
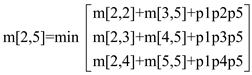
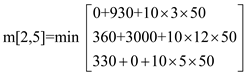
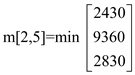
m[2,5] = 2430
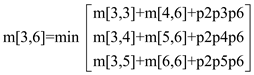
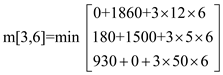
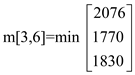
m[3,6] = 1770
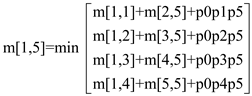
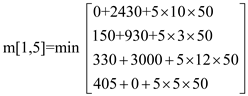
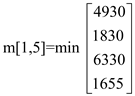
m[1,5] = 1655
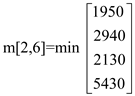
m[2,6] = 1950
m[1,6] = 2010
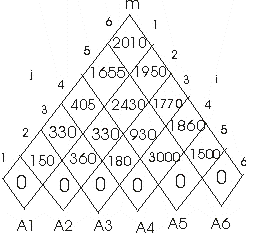
Figure 1
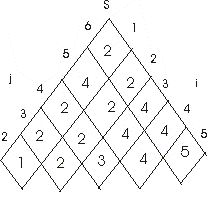
Figure 2
Figure 1 & 2 are m & s tables computed by MATRIX-CHAIN-ORDER FOR n=6
For following matrix dimensions:
|
Matrix |
Dimension |
|
A1 |
|
|
A2 |
|
|
A3 |
|
|
A4 |
|
|
A5 |
|
|
A6 |
|
Minimum cost = 2010
The optimal parenthesization: ((A1 * A2) * ((A3 *A4) * (A5 * A6))) which will need 5*50*6+3*12*5+5*10*3+3*5*6+5*3*6 = 1500 + 180 + 150 + 90 + 90 = 2010
Consider that, A is the sequence of matrices. i.e.
A =
and s
is the table computed by MATRIX-CHAIN-ORDER, which helps to
multiply the sequence of matrices in an optimal way.
The following recursive MATRIX-CHAIN-MULTIPLY
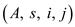algorithm performs the optimal matrix-chain multiplication
of 
MATRIX-CHAIN-MULTIPLY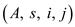
1. if 
2. return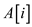 
3. else
//Here LC is a matrix
4. LC = MATRIX-CHAIN-MULTIPLY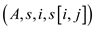
// Here, RC is a matrix
5. RC = MATRIX-CHAIN-MULTIPLY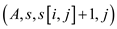
//Result is a matrix that is the result of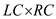 
6. Result = MATRIX-MULTIPLY(LC, RC)
7. return Result
The algorithm for MATRIX-MULTIPLY used in the above algorithm of MATRIX-CHAIN MULTIPLY is as follows:
MATRIX – MULTIPLY (A, B)
1. if columns[A]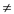
rows[B]
2. then error “incompatible dimensions”
3. else for 
to
rows[A]
4. for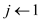 
to
columns[B]
5. 
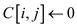
6. for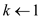 
to
columns[A]
7. 
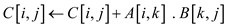
8. return C
The recurrence is given below:
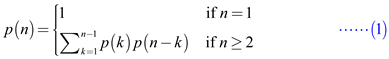
To prove that the solution of the recurrence given in (1) is
,
it is enough to prove that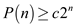 
.
To prove that 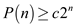, assume
for all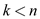 
where
c is the constant.
Substitute different values for n in equation (1) to
calculate the value of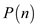 
.
The equation (1) can be divided as follows:
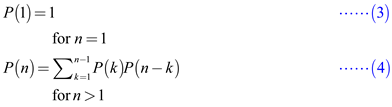
Calculate the value of 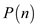for
different value of n greater than 1.
Substitute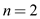 
.
The value of k will be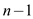 
. So
.
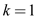Substitute the value of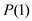 
from
equation (2).
Substitute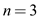 
.
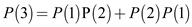
Substitute the values of 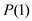and
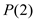from equation (3) and (4)
Similarly calculate the value of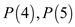 
and so
on.
Substitute previous value of 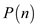is used to
find the next value of .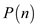
Substitute the value of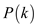 
in equation
(1)
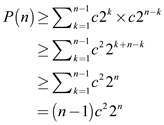
From equation (1)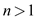 
and
.
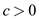So 
.
Hence, .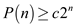
Therefore, the solution of the recurrence given in (1) is
.
Consider the algorithm MATRIX-CHAIN-ORDER,
1. In line 4, the loop can executes n times and line 5
loop can execute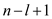 
times.
2. In line 8, the loop can execut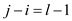es
. m
references two times.
3. The total number of times that m is referenced to compute the other entries is
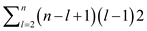
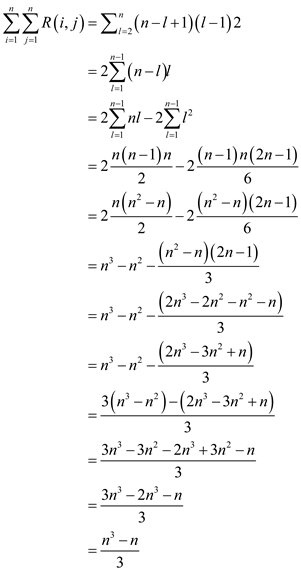
Hence, the total number of references for the entire table
