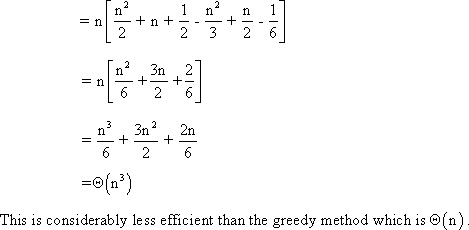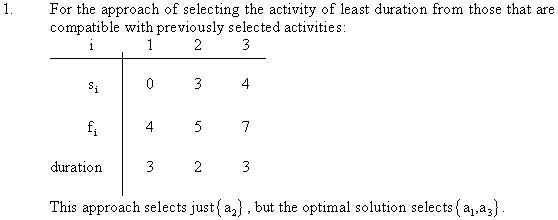Suppose s = {a1, a2,…,an} is a set of activities and each ai = [si, fi). Consider that the activities are sorted by finish time. Now, the goal is to find the largest possible set of non-overlapping of activities by selecting the activities from ending instead selecting from beginning.
Thus, it will become the same if the time is running in reverse and the optimal solution is produced. Since, the best-looking choice is considered so it is greedy.
The following is the algorithm that finds optimal solution by selecting last activity to start:
Proposed Algorithm:
GREEDY-ACTIVITY-SELECTOR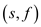
1. n=s.length
2. A={an}
3. k = n
4. for m= n-1 down to 1
5. if f[m] ≤ s[k]
6. A=A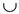 {an}
{an}
7. k = m
8. return A
• The above algorithm takes starting times and finishing times of activities as input. They are sorted by finish time.
• The algorithm initially selects last activity to start first.
• Then the algorithm scans through the activities in descending order and finds a compatible activity to add it to set A.
Since, the above algorithm tries to find an optimal solution in each stage. This approach is obviously a greedy algorithm.
Optimal solution:
Consider s1 is a sub set of {a1, a2, …., an}, is an optimal solution obtained by the approach that selects the first activity to start. s1 can also be obtained by the proposed approach. That is, the solution produced by the approach that selects first activity to start can also be obtained by the proposed approach.
Therefore, the proposed approach also produces an optimal solution.
Solution using GREEDY-ACTIVITY-SELECTOR:
Assume that S be the set of n activities. The
GREEDY–ACTIVITY–SELECTOR finds a maximum size set  of
compatible activities from S.
of
compatible activities from S.
• Since the activities in the set  are
compatible each other, first lecture hall can be allocated to the
activities in
are
compatible each other, first lecture hall can be allocated to the
activities in .
.
• Run the GREEDY–ACTIVITY–SELECTOR again on  to find a
maximum–size set
to find a
maximum–size set 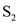 of
compatible activities. Since the activities in the set
of
compatible activities. Since the activities in the set 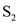 are
compatible to each other, the second lecture hall can be allocated
to the activities in
are
compatible to each other, the second lecture hall can be allocated
to the activities in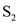 .
.
• Repeat the above step, until the set S-Si is empty.
LECTURE-HALL-SCHEDULER(S)
1 d =1
2 while S ≠ 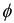
3 Sd = GREEDY–ACTIVITY–SELECTOR(s,f)
4 If Sd ≠ 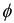
5 Allocate lecture hall d for the activities in the set Sd
6 d= d+1
7 S= S-Sd
Where, s and f are the starting and finishing times of activities in the set S.
LECTURE-HALL-SCHEDULER() runs the while loop in 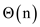 in the worst
case. And the GREEDY–ACTIVITY–SELECTOR() runs in
GREEDY–ACTIVITY–SELECTOR(s,f).
in the worst
case. And the GREEDY–ACTIVITY–SELECTOR() runs in
GREEDY–ACTIVITY–SELECTOR(s,f).
Hence the above simple algorithm requires  time
in the worst case.
time
in the worst case.
Alternative greedy algorithm:
There is a better algorithm that schedules the activities in few
lecture halls in the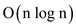 .
.
• Here, the idea is to go through the activities in order of start time, and assigning each activity to any lecture hall that had already a scheduled activity and it is available at the starting time of the activity.
• If no such lecture hall is found, schedule the activity in a new lecture hall. This guarantees that the algorithm uses as few lecture halls as possible and all the activities in a lecture hall are compatible.
• Thus, this problem can be compared with the interval-graph coloring problem. In the interval-graph coloring problem, all the activities or intervals, which are compatible, are colored with the same color such that the no two incompatible activities (vertices) have the same color.
The algorithm will terminate when all the activities are scheduled to any one of the lecture hall. Assume S has the activities that are sorted by start time.
LECTURE-HALL-SCHEDULER(S)
1 k =1 // initially, first activity a1 is scheduled in lecture hall Hk = H1.
2 for i = 2 to n
3 if ai is compatible with activities in some lecture hall Hk
4 then schedule the activity ai in the lecture hall Hk
5 else
6 Schedule the activity ai in the new lecture hall Hk +1
7 k= k+1.
Running time:
The above algorithm schedules all the given activities in few lecture halls in O (n log n) time for arbitrary times. The algorithm may possibly run in O (n) if the times are small integers.
Modification for Activity selection problem:
• In this problem, each activity contains
three variables and
contains
three variables and 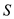 is the set
of start times of
is the set
of start times of 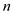 activities
that are to be completed.
activities
that are to be completed.
• 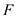 be the set
of finish times of
be the set
of finish times of 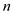 activities
that are to be completed and
activities
that are to be completed and 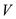 be the set
of all the activity values.
be the set
of all the activity values.
• The objective of this problem is to choose the activities from the set such that the working times of these activities are not same and the variable V can have the maximum value.
• That is, for the set, which contains the final activities selected, the sum of the values of the activities in the set should be maximum.
• Greedy Algorithm is dependent on greedy choice.
• In each step choose greedy optimal choice from set of input available.
Activity selection procedure:
• First sort the activity:
• Sort activity on the basis of their finishing time, such that activity which takes less time must be available first.
• Select least time taking activity and store it.
• For each activity element:
• Select next least finishing time activity and store it.
• The activities are chosen from a set of activity such that they can be performed at the same time without any conflict.
• It means only those activities, which can be done by only one person at a time, are selected.
• The optimal solution for this problem can be found by finding the maximum value that could be reached and then by including the activities that contributed to it in the solution set.
• The sub routine 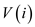 = the
maximum value that can be reached by including activities that end
only after the
= the
maximum value that can be reached by including activities that end
only after the 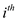 second.
second.
• Arrange the activities in decreasing order by their finish
times. Now, either the maximum value could be reached by including
the 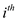 activity or
by including activities after it that do not overlap with the
activity or
by including activities after it that do not overlap with the
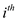 activity.
activity.
Algorithm:
• Let as[i] be the maximum total value before the time i, which is given below:
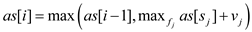
• Here, f[] is used for storing finish time, and s[] is used to store start time of each activity.
Polynomial time algorithm:
1. FUNCTION ACTIVITY_SELECTION(s, f, v)
2. as = {}
3. n = length (s)
4. last = empty
5. for each i in sorted(list(set(s + f))):
6. if last is empty:
7. as[i] = 0
8. else
9. as[i] = last
//l is length of s[]
10. int x=find((f[j],s,l)
11. for(int y=o;y<x;y++)
11. If f[j] < s[i]:
12. as[i] = max(as[i], as[s[j]] + v[j])
13. last = as[i]
14. return last
1. FUNCTION find(f[j],s,l)
//binary Search would return index
2. int i= binarySearch(s,f[j};
3. return i;
Hence, the time complexity of the algorithm is O(nlogn).