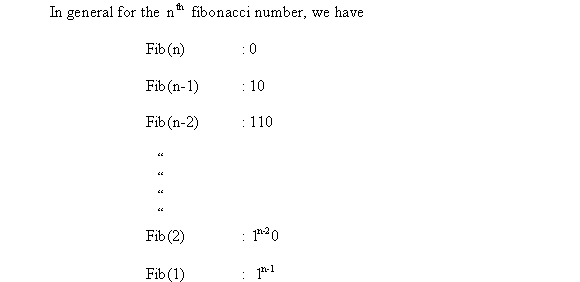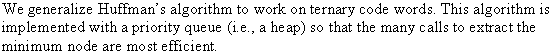 is
is
 and
if the characters x and y are the characters with
minimum occurrences in the set. The prefix code for
and
if the characters x and y are the characters with
minimum occurrences in the set. The prefix code for 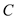 is optimum
for which x and y are of same length with the
difference in the last bit.” The prefix code is the code which is
not the prefix of any other code.
is optimum
for which x and y are of same length with the
difference in the last bit.” The prefix code is the code which is
not the prefix of any other code.Consider the alphabet or string C made up of characters x, and y. As x and y are the elements with lowest frequencies, in-order. The two character a and b in C are such that
 …… (1)
…… (1)
Now, because the frequency of x and y are the least in the entire alphabet in-order then,
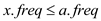 …… (2)
…… (2)
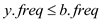 …… (3)
…… (3)
From equation (1), (2) and (3)
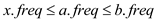 …… (4)
…… (4)
As from Lemma, y has the second lowest frequency so
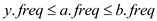 …… (5)
…… (5)
From the equations (4) and (5)
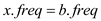
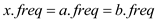
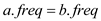
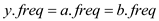
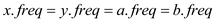
Hence it proves that in the lemma “In an alphabet the frequency
of a character 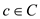 is
is
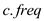 and
if the characters x and y are the characters with
minimum frequency in the set. The prefix code for
and
if the characters x and y are the characters with
minimum frequency in the set. The prefix code for 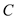 is optimal
for which x and y are of same length with the
difference in the last bit.” if
is optimal
for which x and y are of same length with the
difference in the last bit.” if 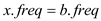 then,
then,
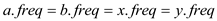 .
.
Full binary tree is a tree in which each node has two children except the leave node. In binary code word left child of any node is represented by 0 and right child of node is represented by 1.
• Consider a tree T that is not a full binary tree. Since the tree is not full so there is a node n that have only one child node x.
• The edge between the node n and x, add the bit either 0 or 1 in prefix code.
• In order to get the optimal prefix code if someone remove the edge and replace node n with x, thus the length of prefix code is reduced by one. It means the tree after removing the edge represent same alphabet with a lower cost.
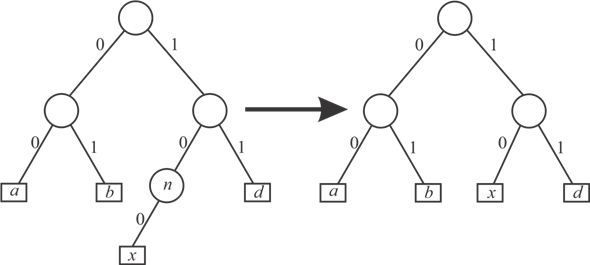
Hence, the binary tree that is not full cannot correspond to an optimal prefix code.
Consider the following diagram that is not full binary tree to prove a binary tree that is not full cannot correspond to an optimal prefix code.
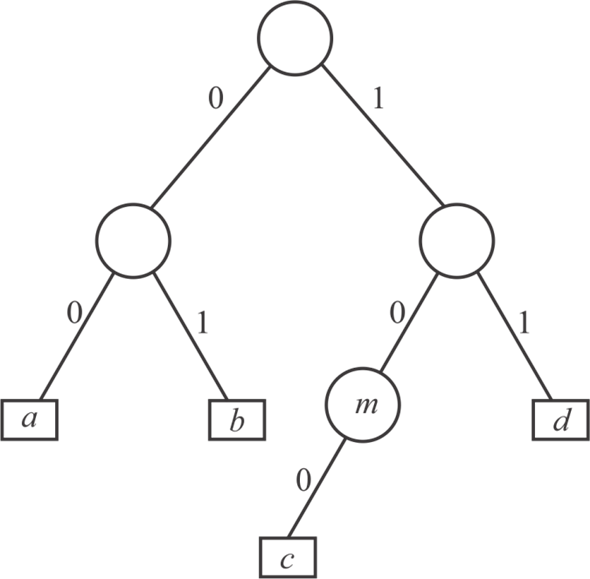
Figure-1
• In the above Figure-1 each character is represented by
a unique binary string such as: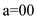 ,
,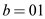 ,
,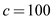 and
and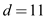 .
.
• In this binary tree each character has variable length, here the two bit string represent a, b and d, and the three bit string 100 represent c.
• In order to get optimal prefix code, remove the edge between m and c and replace m by c.
Figure-2
Since the Figure-2 is full binary tree and the length of character c is reduced by 1, so the binary string for character c will be 10.
Hence, the binary tree that is not full cannot correspond to an optimal prefix code.
The idea of the proof is to take the tree T, with n leaves on representing the induction hypothesis. The induction hypothesis applies on the number of leaves in T.
Consider that the case, when n=1, it means trivially true to representing the tree in optimal frequencies.
The different Case when n = 2 and let the x and y two characters appears as a leaf with the root(parent) node C, then the cost of the tree T is as shown below:

Hence, the above statement is proved the theorem is true for n=2.
Consider that n > 2 and check the theorem is true for n> 2 or not for the tree on n-1 leaves.
Consider a and b are the two leaves of the parent root node c. After deleting the node, a and b, assume the tree is obtained T’ by the induction method:
from the induction theorem, the tree is concluded that:

Thus, using from the above information, compute the cost of the tree T.



Thus, from the above computation is concluded that the theorem statement is true for n>2 also.
Hence, from the above cases n =1, n =2, and n > = 2 is concluded that the tree for a code as the sum, all over the internal nodes, is the combined frequencies of the two children of the node. It has expressed as the total cost of the tree.
Consider the all alphabet C in decreasing order such that
each character  with an
attribute
with an
attribute .
.
Since optimal code for codeword is represented by full binary tree and each node of full binary tree is defined by level number.
Consider the following diagram to prove, if all character are arrange in decreasing order of frequency then the codeword length increases monotonically.
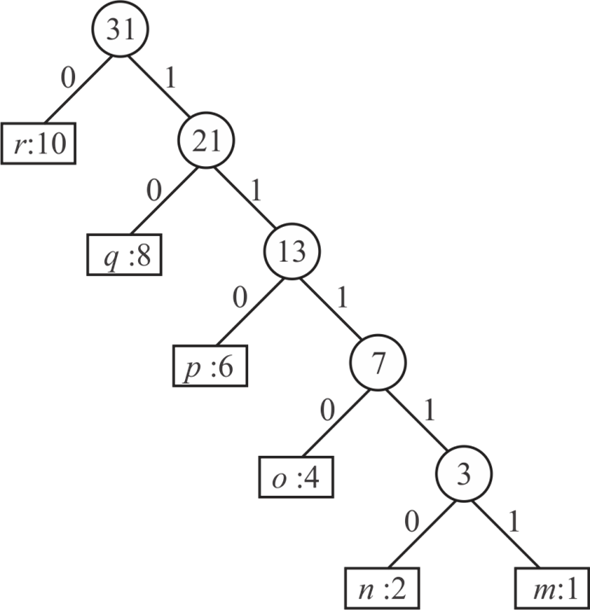
• In the above diagram leaves node are represented by rectangles and contaings a character and its frequency.
• All internal nodes are represented by circles and containing the frequency of their children.
In the above diagram each character is arranged in descending order according to their frequency so the frequency of each character is as follows:
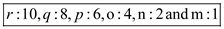 …… (1)
…… (1)
In binary code word left child of any node is represented by 0 and right child of node is represented by 1 so each character of above diagram is represented by a unique binary code-word such as:
 ,
, ,
, ,
,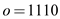 ,
,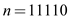 and
and
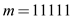 ……(2)
……(2)
Here the length of each character is increased monotonically.
In equation (1) all character are arrange in descending order and equation (2) show the length of each character that monotonically increased.
Hence, from equation (1) and equation (2) it clear that if all character are arrange in descending order of their frequency then there exist the optimal code whose code-word is monotonically increase.
8-bit fixed length coding:
Consider that the file contains characters of 8-bit code. That is, each character is represented using 8-bit fixed length.
Then, if the file contains n characters, the cost (number of
bits to encode all the characters) is 8n bits. 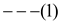
Huffman coding:
It is known that the Huffman algorithm always generates a full binary tree and assigns prefix code to each character.
• Consider that a data file has k different characters
and 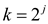 .
.
• Consider that the maximum character frequency and minimum character frequency are Fmax and Fmin respectively.
• If the data file has the characters such that, 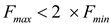 , then the
Huffman algorithm generates a complete binary tree with all the
leaves will have depth j .
, then the
Huffman algorithm generates a complete binary tree with all the
leaves will have depth j .
• Since, each character has depth j, each character requires j bits to be encoded.
It is given that the data file has 256 different characters.
k=256=28 and the file has the characters such
that 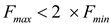 .
.
Therefore, the Huffman algorithm generates a complete binary tree and all the 256 characters have depth 8.
Since each character has A depth 8, each character requires 8 bits to be encoded.
The cost to encode all the characters(n) in the file =
8n 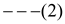 .
.
From (1) and (2), it is clear that the Huffman coding is not efficient than ordinary 8-bit fixed-length code.
Hence, Huffman coding is not efficient than fixed length
code, if the data file contains characters such that
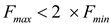 .
.