A matroid set is defined as the ordered structure 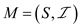 which
fulfills the following conditions:
which
fulfills the following conditions:
1. The set S must be a finite set.
2. The set 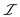 contains at
least one value in it and is formed from the sub-sets of S
such that if
contains at
least one value in it and is formed from the sub-sets of S
such that if 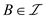 and
and
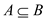 then
then .
If it satisfies this property then
.
If it satisfies this property then 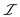 is called as
hereditary.
is called as
hereditary. 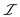 Must contain
empty set
Must contain
empty set .
.
3. If ,
, 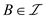 and
and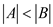 then for an
item
then for an
item 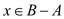 such
that
such
that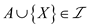 . It is
called as exchange property.
. It is
called as exchange property.
Proof of first property:
It is already given that in , S
is a finite set so that it follows the (1) property of matriod.
, S
is a finite set so that it follows the (1) property of matriod.
Proof of second property:
It is also given that  is a set
which contain all the subsets of S. This implies that
is a set
which contain all the subsets of S. This implies that
 also contain
the empty set
also contain
the empty set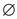 .
.
Suppose B is a subset of S which lies in  and
also
and
also . Therefore,
A is also a subset of
. Therefore,
A is also a subset of . This can
be shown by following example:
. This can
be shown by following example:
Suppose S is a finite set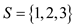 .
.
Therefore all the subset of S that lies in  are as
follow:
are as
follow:
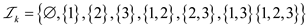
Suppose B is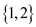 and A
is subset of B so A can be
and A
is subset of B so A can be 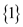 or
or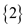 . The subset
A is also a member of
. The subset
A is also a member of .
Therefore
.
Therefore satisfies
the 2nd property of matriod.
satisfies
the 2nd property of matriod.
Proof of third property:
Suppose A is 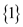 and B
is
and B
is 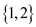 are the subset lies in
are the subset lies in . The number
of elements in A is less than B that is
. The number
of elements in A is less than B that is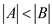 . There
exist element x which exist in B but not in A
that is element 2. The subset
. There
exist element x which exist in B but not in A
that is element 2. The subset 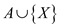 that is
that is
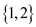 is
also a part of
is
also a part of .
.
Therefore satisfies
the 3rd property of matriod.
satisfies
the 3rd property of matriod.
The  satisfies all three properties of matriod.
satisfies all three properties of matriod.
Therefore,  is a
matriod.
is a
matriod.
A matroid set is defined as the ordered structure 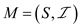 which
fulfills the following conditions:
which
fulfills the following conditions:
1. The set S must be a finite set.
2. The set 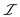 contains at
least one value in it and is formed from the sub-sets of S
such that if
contains at
least one value in it and is formed from the sub-sets of S
such that if 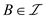 and
and
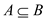 then
then .
If it satisfies this property then
.
If it satisfies this property then 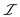 is called as
hereditary.
is called as
hereditary. 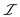 Must contain
empty set
Must contain
empty set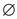 .
.
3. If ,
, 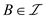 and
and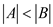 then for an
item
then for an
item 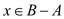 such
that
such
that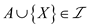 . It is
called as exchange property.
. It is
called as exchange property.
The following three conditions must be satisfied in order to
show 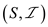 is
Metroid:
is
Metroid:
• S is a finite set; it is because S contains the set of columns of T.
• Suppose 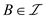 , therefore
the column of B matrix are linearly independent. If A is
subset of B that is
, therefore
the column of B matrix are linearly independent. If A is
subset of B that is . Then,
A must be linearly independent therefore,
. Then,
A must be linearly independent therefore,  .
.
Hence, 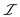 is
hereditary.
is
hereditary.
• In order to proof the exchange property, suppose A and
B are subset of 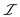 and
and
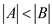 .
.
The columns of A are linearly independent. Now, in order to calculate the rank takes these columns as matrix. The maximal set of linear independent columns is the rank of any matrix. Therefore the rank of A becomes:
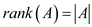
Similarly, the rank for B becomes:
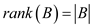
Because, 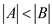 therefore
therefore
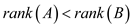 …… (1)
…… (1)
Use contradiction to proof the exchange property that is
there is column d in B which does not form linearly
combination with columns of A. Therefore 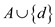 is linearly
independent.
is linearly
independent.
At first suppose the columns of B form linear combination with columns of A. This means the column space of B form subspace for columns space A.
So, according to matrix property that if column space of
X is subspace of Y then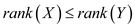 .
.
Therefore, rank of B is less than rank of A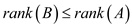 . This
contradicts the equation (1). So, B’s columns are not linear
combination of A’s column.
. This
contradicts the equation (1). So, B’s columns are not linear
combination of A’s column.
Therefore, 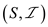 satisfies
the exchange property. The,
satisfies
the exchange property. The,  satisfy all
three properties of matriod. Hence
satisfy all
three properties of matriod. Hence  is a
matriod.
is a
matriod.
It is required to show that if (S, I) is a matroid, then
(S,  ) is a
matroid. So, first show that
) is a
matroid. So, first show that  is
non-empty. Let the maximal element of
is
non-empty. Let the maximal element of  be A, then
be A, then
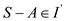 because S-(S-A) =
because S-(S-A) = 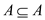 which is
maximum in
which is
maximum in  .
.
Suppose that 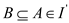 , then there
must exist
, then there
must exist 
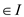 so that
so that
 ,
however S-B
,
however S-B
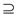
 so
so 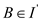
Lastly, the exchange property is required to be proved. If B
exists, 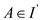 and
|B|<|A|, so an element y can be found out in A-B that can be
added to B. In this scenario, there exists two cases:
and
|B|<|A|, so an element y can be found out in A-B that can be
added to B. In this scenario, there exists two cases:
Case 1: |A|=|B|+1
Case 2: Let X be a maximal independent set of I which is
contained in S-A. Pick a set having size |X|-1 from the
independent set contained in S-B, let the set be Y. So there
exists some 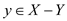 such that
such that
 is
maximal independent set in I
is
maximal independent set in I
Thus,  is
independent in
is
independent in 
Consider a finite set S which is to be partition into
number of subsets  with at
least one element in them now defining a structure
with at
least one element in them now defining a structure 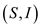 such
that
such
that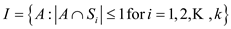 . Proving
that the structure
. Proving
that the structure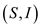 is
matroid.
is
matroid.
Matroid set is defined as the ordered structure 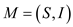 which
fulfills the conditions as:
which
fulfills the conditions as:
1. The set S in matroid set is finite.
2. The set I contains at least one value in it and is
formed from the sub-sets of S such that if 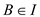 and
and
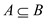 then
then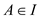 .
.
3. If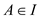 ,
, 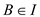 and
and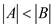 then for an
item
then for an
item 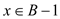 such that
such that
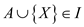
For a set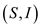 to be a
matroid set it must fulfill the properties of the matroid set which
is as follows:
to be a
matroid set it must fulfill the properties of the matroid set which
is as follows:

Now, 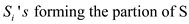 , after that
the rank of the function is as given below:
, after that
the rank of the function is as given below:

Thus, the rank function of the matroid is as follow some properties is as given below:
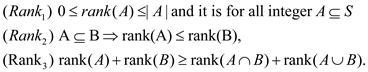
Thus, from the above three functions, concluded that the following cases is as follows:
1. 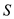 is a finite
non-empty set. (Non-empty because the partitions of
is a finite
non-empty set. (Non-empty because the partitions of 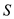 are
non-empty)
are
non-empty)
2.  is
non-empty, as mentioned in the problem. If
is
non-empty, as mentioned in the problem. If 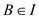 , then
, then
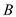 contains
either one or no element from the partition. And any subset of
contains
either one or no element from the partition. And any subset of
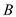 will also,
therefore contain either one or no element from the partition. So,
will also,
therefore contain either one or no element from the partition. So,
 is
hereditary.
is
hereditary.
3. If 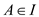 and
and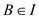 and
and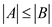 , which
means
, which
means 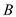 has at
least one element more than
has at
least one element more than 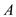 . This
element must belong to some partition of
. This
element must belong to some partition of 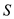 whose
element is not in set
whose
element is not in set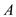 (as
(as
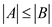 ).
If such an element is added to
).
If such an element is added to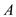 , it will
still fulfill the property of
, it will
still fulfill the property of  containing
at most one element from a partition.
containing
at most one element from a partition.
Since the structure 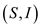 fulfills
all the properties of the matroid set so
fulfills
all the properties of the matroid set so 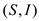 is
matroid.
is
matroid.
Hence the structure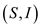 , made up of
the finite set S which is to be partition into number of
subsets
, made up of
the finite set S which is to be partition into number of
subsets  with at
least one element in and
with at
least one element in and 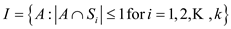 is
matroid.
is
matroid.
Transforming the weight function of a weighted matroid problem to a standard weighted matroid problem:
The weighted Matroid set is defined as the ordered structure
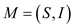 with weight function
with weight function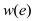 which
fulfills the conditions:
which
fulfills the conditions:
1. The set S in matroid set is finite.
2. The set I contains minimum one value in it and is
formed from the sub-sets of S such that if 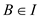 and
and
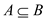 then
then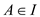 .
.
3. If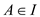 ,
, 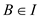 and
and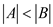 then for an
item
then for an
item 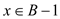 such that
such that

• The input to the GREEDY algorithm that solves matroid problem
is a set  and
and , and it
returns an optimal independent subset
, and it
returns an optimal independent subset 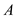 such that
such that
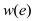 is
maximized.
is
maximized.
• The algorithm considers each element  in the order
of non-increasing weight and adds it to the solution set
in the order
of non-increasing weight and adds it to the solution set 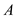 , if
, if
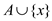 is
independent.
is
independent.
• Now, the new weights function as follows:

• Here, is a number
greater than the highest weight of any of the edges in the
graph.
is a number
greater than the highest weight of any of the edges in the
graph.
• Now, all 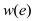 for a
matroid with positive edges are zero. So, as the value
for a
matroid with positive edges are zero. So, as the value 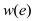 increased
the value of
increased
the value of  is
decreased, because
is
decreased, because  is
constant.
is
constant.
Hence, any algorithm that will maximize weight function
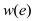 will
minimize
will
minimize  that
is the standard weight function.
that
is the standard weight function.