Insertion Sort:
It is one of a sorting technique which is used to sort the elements of list in particular fashion. In insertion sort a single list is divided into list: sorted and unsorted list. In starting sorted list is empty, in each step one element is taken from the unsorted list and put it in proper place in sorted list.
The worst case complexity of insertion sort is . It means
insertion sort takes maximum
. It means
insertion sort takes maximum  time to
sort a list having n elements. The time taken by insertion
sort to sort
time to
sort a list having n elements. The time taken by insertion
sort to sort 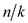 lists each
having k elements is
lists each
having k elements is

The worst-case time complexity of insertion sort to sort
the 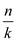 sub
lists each of length k is
sub
lists each of length k is 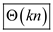 .
.
If user uses 2-list merge to merge all lists it would take
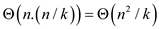 time because then user need n time to copy each element and
create a new sorted list. Also there are of total n/k list
to be merged.
time because then user need n time to copy each element and
create a new sorted list. Also there are of total n/k list
to be merged.
But to achieve 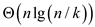 time, one
can use pairwise merging. So, user starts with initial lists and
makes pairs of them and merges them. After this step there are some
resultant lists which are sorted. Then again user does the same to
those resultant lists by applying pairwise merging and this process
will go on till user will end up with a single list.
time, one
can use pairwise merging. So, user starts with initial lists and
makes pairs of them and merges them. After this step there are some
resultant lists which are sorted. Then again user does the same to
those resultant lists by applying pairwise merging and this process
will go on till user will end up with a single list.
Since merging needs  time at
each level and there are of total of ceil
time at
each level and there are of total of ceil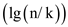 height
of tree because at starting the number of list starts with
n/k. So, the total running time for merging is
height
of tree because at starting the number of list starts with
n/k. So, the total running time for merging is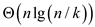 .
.
Therefore, using the above process it is possible to merge
sub lists in 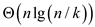 worst case time.
worst case time.
The complexity of modified algorithm is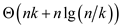 . The worst
case complexity of merge sort is
. The worst
case complexity of merge sort is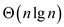 .
.
In modified algorithm the largest value of k should not
be more than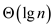 , in order
to make complexity equal to merge sort.
, in order
to make complexity equal to merge sort.
The value of k should not be more than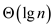 ,
,
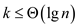
Now put 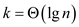 in modified
algorithm complexity
in modified
algorithm complexity
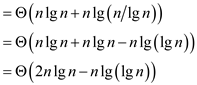
Here ignoring constant and taking the higher turn will give the
complexity 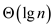
Now to check that it is the maximum value for k, assume
the value for k greater than 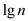
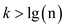 …… (1)
…… (1)
Multiply by n on both sides, the equation (1) will become
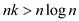 …… (2)
…… (2)
From equation (2), the complexity will become,
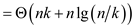
Ignore lower term.
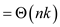
But this contradicts the condition that the complexity cannot exceed the running time of original merge sort.
Hence the value for k should not be
greater than 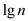 .
.
Since it is a constant factor, so user must select the value of k for which merge sort takes more time than insertion sort. Also this value will vary from computer to computer.
A bubble sort is a sorting algorithm which is used to arrange elements of an array in ascending or descending order. In each iteration, the algorithm checks adjacent elements to determine whether the first element is smaller than later element or not, if not, elements are exchanged.
Two prove that bubble sort is correct, the output array must be in sorted order and the elements in the output array must be the elements in the original elements in A (irrespective of their order).
• Since it is already given that the output array  contains
the sorted elements, it is enough to prove
contains
the sorted elements, it is enough to prove  contains
all the elements of A.
contains
all the elements of A.
• In other words, it is enough to prove that one of the
permutations of A is same as .
.
A loop invariant is any condition or value of any variable in a program that must be true before and after each iteration of any loop.
• The goal of for loop in lines 2-4 is to place the least element of the sub array A[i,n] at ith position.
• At the start of each iteration of for loop defined in line 2-4, the sub-array A contains elements of A but only in index between j and n.
• At the end or start of for loop from line 2-4, the jth position contains the smallest element between j and n.
Initialization:
In starting of ‘for’ loop defined in line 2-4, the value
of j is equal to n. The sub array A contains
only one element 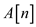 which is
smallest among j and n. Therefore the loop invariant
trivially holds.
which is
smallest among j and n. Therefore the loop invariant
trivially holds.
Maintenances:
• The 3rd line compares the jth and j-1th element of array A in each iteration of for loop. When the jth element is smaller than j-1th element, then the 4th line of BUBBLESORT() algorithm swaps these two elements.
• Swapping will not alter the permutation so loop invariant will hold true.
• At the end of each iteration, the ith position contains the smallest element between j and n, because the last comparison happens between, jth and ith elements.
• Decreasing the value of j after every iteration will maintains the invariant.
Termination:
• The ‘for’ loop terminates when value of j becomes equal to i.
• After the termination of inner for loop the ith index contains the smallest element between i and n.
Loop invariant:
In each iteration of for loop defined in line 1-4, the
sub-array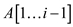 contains
i-1 elements in ascending order.
contains
i-1 elements in ascending order.
Initialization:
In starting of ‘for’ loop defined in line 1-4, the value
of i is equal to 1. The sub array 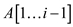 does not
contain any elements. Therefore the loop invariant holds.
does not
contain any elements. Therefore the loop invariant holds.
Maintenances:
• According to part (b), the inner for loop defined in line 2-4, stores the smallest element at i.
• Also, in each iteration, i value is incremented by 1.
• That is, after ith iteration, sub
array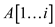 contains
i number of smallest elements of array
contains
i number of smallest elements of array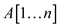 , in sorted
order.
, in sorted
order.
Termination:
• The outer ‘for’ loop terminates when the value of i becomes equal to n-1.
• That is, after the termination of the outer for loop,
the array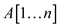 contains the
elements of original array
contains the
elements of original array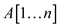 in sorted
order.
in sorted
order.
• The running time of any algorithm depends on number of times the basic operation executes.
• In BUBBLESORT() algorithm two for loops are used to compare elements(basic operation).
• The iteration of inner for loop defined in line 2-4 depends on the value of i.
When value of i is 1 then inner for loop iterates
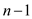 times, similarly when value of i is 2 then inner for
loop iterates
times, similarly when value of i is 2 then inner for
loop iterates 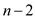 times. So,
for i the inner for loop iterates
times. So,
for i the inner for loop iterates 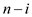 times
times

Add and subtract n


Hence, the running time of BUBBLESORT () algorithm
becomes  ,
because n 2 is the
dominant.
,
because n 2 is the
dominant.
Comparison with Insertion sort:
• Consider the insertion sort algorithm provided in section 2.2.
The running time of insertion sort in worst case is also
 and in
the best case the complexity is reduced to
and in
the best case the complexity is reduced to .
.
• In the bubble sort mentioned above, the complexity will remain
same that is  in both
worst and best cases.
in both
worst and best cases.
Correctness of Horner’s rule
a) Line 1 executes only one time to initialize the value of y to zero.
Line 2 executes n times as the single for loop goes from n to 0.
Line 3 executes 1 times.
The running time is 1+n+1=n+2.
Hence the running time of the given code for Horner’s rule in terms of Θ-notation
is Θ(n).
b) PSEUDOCODE for NAIVE polynomial – evaluation algorithm is
NAIVE-POLY-EVAL(P, x):
1. y ← 0
2. for i ← 0 to length(P)
3. do ai ← P[i]
4. z ← 1
5. for j ← 1 to i
6. do z ← x·z
7. y ← y + ai·z
8. return y
Here y will contain the coefficients of the polynomial P.
Running time of NAIVE polynomial – evaluation algorithm is the Θ(n2). There
are two for loops. The inner for loop executes for n times and outer for loop executes for n times. Hence the running time of this algorithm is Θ(n2).
The running time of Horner’s rule is Θ(n) whereas the running time of NAIVE
polynomial – evaluation algorithm is the Θ(n2).
c) The loop invariant proofs consist of three parts: Initialization, Maintenance and
Termination.
Initialization: Initialize y = 0 and i = n at the beginning of the loop. i
Maintenance: For each iteration of the loop, 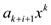 is
calculated and is assigned to y and in the next loop
iteration the value y is used as a coefficient to
x.
is
calculated and is assigned to y and in the next loop
iteration the value y is used as a coefficient to
x.
Termination: When the loop terminates with a condition i < 0 and when the last iteration finishes, the ‘i’ value becomes less than 0. When the loop terminates, i = -1 and at that iteration the y value becomes
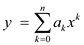
d) To conclude that the given code correctly evaluates a polynomial, let take an
example.
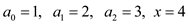
According to Horner’s rule the polynomial evaluation will be as follows.
Step 1: 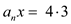
= 12
Step 2: 
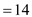
Step 3: 
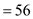
Step 4: 

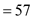
Usual Polynomial Method of Evaluation

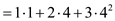
=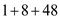
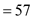
Thus it can be concluded that Horner’s rule correctly evaluates a polynomial equation.
Consider an array 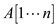 of n
distinct elements. Pair
of n
distinct elements. Pair 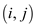 is called
an inversion of array
is called
an inversion of array 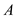 if the
condition
if the
condition 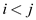 and
and
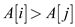 is
satisfied.
is
satisfied.
a)
Consider an array 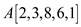 to
calculate the inversion.
to
calculate the inversion.
Take 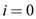 and
and
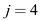 (index start with 0).
(index start with 0).
Then 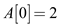 and
and
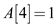 .
.
According to the definition of inversion 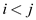 and
and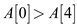 .
.
So the pair of inversion will be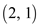 .
.
Similarly, the remaining four inversions are 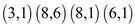 .
.
Therefore, all the five inversions are as follows 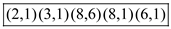 .
.
b)
Arrange the elements in the set in reverse and store them in the array.
The elements in the array in reverse order are  . This array
has most inversion.
. This array
has most inversion.
Calculate the total number of inversion in array  is as
follows:
is as
follows:
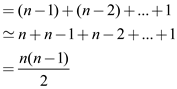
Where first element has 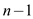 inversion
and second element has
inversion
and second element has 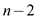 inversion
and so on.
inversion
and so on.
c)
Relationship between the running time of insertion sort and the number of inversions in input array:
• In insertion sort every unsorted element 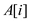 of array is
swapped by adjacent element
of array is
swapped by adjacent element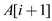 .
.
• The process of insertion sort decreases the number of
inversions in array A, because the element at location
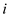 and
and 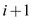 will no
longer is an inversion.
will no
longer is an inversion.
• If array 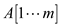 has
k inversion with
has
k inversion with 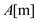 then the
element before m are sorted.
then the
element before m are sorted.
• Total number of iteration required in insertion sort is
 and inversion is perform only when
and inversion is perform only when 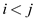 and
and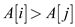 .
.
• So finally running time is 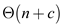 where
c indicates the number of inversion because inversion is
required only for unsorted data.
where
c indicates the number of inversion because inversion is
required only for unsorted data.
d)
Modified merge sort algorithm is to determine the number of inversion in n permutation.
MERGE–SORT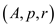
// p is the starting point of array and r is the last index.
1. If 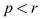
// set the value of inversion
2. Inversion= 0
//calculate the value of q
3. 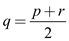
// find the value of inversion where A is the Array name
4. inversions= inversions+ MERGE–SORT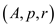
5. inversions= inversions+ MERGE–SORT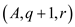
6. inversions= inversions+ MERGE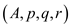
// return the inversion
7. return inversions
// else part execute when if part is false
8. else
9. return 0
MERGE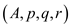
//store the value in variable  .
.
1. 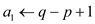
//store the value in variable 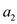
2. 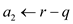
// take two new array 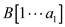 and
and
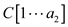
3. for 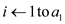
// store the value of array A at ith location of array B
4. 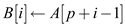
5. for 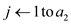
6. 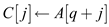
// initialize the value of i and j
7. 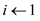
8. 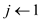
//another for loop is used to traverse from p to r
9. for 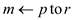
//if index i is greater than 
10. if 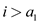
//copy the content of array B into array A
11. 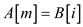
// increment the value of j by 1
12. j++
//if index j is greater than 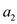
13. else if 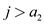
//copy the content of array B into array A
14. 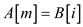
// increment the value of j by 1
15. i++
16. else
17. 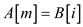
18. j++
//find the inversion
19. inversions= inversions
20. return inversions
Explanation of algorithm:
• Merge sort algorithm uses the index values of the array.
• If initial index is less than the final array then initialize the value of inversion.
• Calculate the value of q.
• Find the value of inversion according to the line number 4, 5 and 6 of merge short algorithm.
• Next algorithm is used to count total number of inversion.
• Two new arrays are used to store the temporary value of explicit array.
• Different for loop is used to count the inversion at all specific value of array.