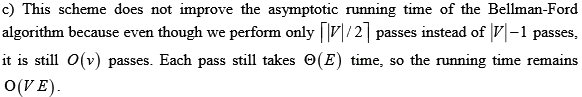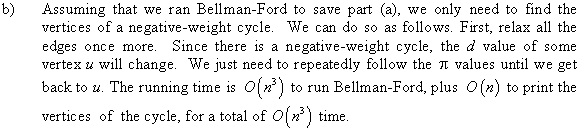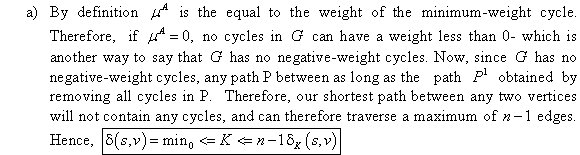a)
Consider the boxes with dimensions:  and
and
 .
Suppose there exists a permutation
.
Suppose there exists a permutation 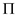 such that
such that
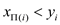 for
for 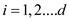 and there
exists a permutation
and there
exists a permutation  such that
such that
 for
for 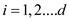 so that
x nests inside y and y nests inside
z.
so that
x nests inside y and y nests inside
z.
Construct a permutation 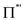 , where
, where
 .
Then for
.
Then for 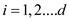 ,
,  and so
x nests inside z.
and so
x nests inside z.
b)
A box X with sorted dimensions  nests inside
a box Y with the sorted dimensions
nests inside
a box Y with the sorted dimensions 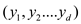 and only if
and only if
 for
for 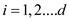 that is, the
dimensions of x are component-wise less than the increasing
sequence of dimensions of y.
that is, the
dimensions of x are component-wise less than the increasing
sequence of dimensions of y.
To prove that a one-dimensional box nests inside another or not, do the following:
• Sort the dimensions of each box from the longest to shortest
and the sorting can be done in 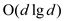 time.
time.
• Since, each box is compared sequentially such that  in
in
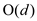 time,
so the orientation of the boxes is possible.
time,
so the orientation of the boxes is possible.
c)
To find the longest sequence of boxes the algorithm is as follows:
• Sort each box in 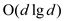 time using
radix sort and find the relations to prove that the boxes are
nested inside each other. If the box
time using
radix sort and find the relations to prove that the boxes are
nested inside each other. If the box  nests
inside
nests
inside  then draw
the arrow from
then draw
the arrow from  to
to
 otherwise
do vice-versa.
otherwise
do vice-versa.
• Do the pairwise comparison in 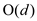 time, such
that
time, such
that  , for each
of the
, for each
of the  pairs.
pairs.
Thus, a partial relation is produced and a DAG (Directed Acyclic
Graph) is obtained in  time which
finds the longest path. Thus, the total running time is:
time which
finds the longest path. Thus, the total running time is: 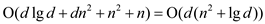 . It
includes the summation of the time obtained by sorting, for
pair-wise comparison and for each of the pairs.
. It
includes the summation of the time obtained by sorting, for
pair-wise comparison and for each of the pairs.
a)
Here, Dijkstra’s algorithm can be used since all the edges are positive to find the shortest path from the start vertex to all vertices. The running time of Dijkstra’s algorithm using a binary heap is O(E lg V). The term lg V comes from the V calls to extract min and the E calls to decrease the key.
It is given that the edge weights are integers and the shortest path is given by |E|, the running time can be much better. The counting sort method can be used to main the list of vertices. It is known that the weights of the path to each vertex are always an integer between 0 to |E|. Maintain an array SHORT of linked list for each possible value, INSERT, KEY_DECREASE, and MIN_EXTRACT functions.
Inserted vertex which is reachable in length I, are added to the beginning of the linked list SHORT[i], which is O(1).
KEY-DECREASE function on vertex v is invoked by removing v from its current linked list, decrease it key to i, and insert it into SHORT[i] for the total time of O(1).
MIN –EXTRACT always extract vertices with shortest paths of non-decreasing value. The actual extraction time is O(E). Since, there are E lists, scanning for a non-empty list could take time of O (E).
Since, there is no backtracking for scanning, this O(E) scan of lists is averaged to O(V) calls to MIN_EXTRACT. The amortized cost is O(E/V) each list.
Therefore, the total running time includes V calls to INSERT(O(V)), E calls to KEY_DECREASE(O(E)) and V calls to MIN_EXTRACT(O(E+V)) for total running time of O(E+V). Since, |E| > |V|-1, the running time is O(E).
b)
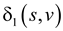 is computed by using the edge weight function w1, which
uses the first significant bit of the edge weights. The weights of
w1 are either 0 or 1.
is computed by using the edge weight function w1, which
uses the first significant bit of the edge weights. The weights of
w1 are either 0 or 1.
The maximum number of edges on as shortest path is |V|-1. if the weight of w1 is equal to 1 then the maximum weight of a shortest path is |V|-1.
Therefore, 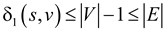 for all
vertices v
for all
vertices v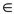 V. From (a)
it is shown that
V. From (a)
it is shown that 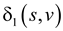 can be
computed in O(E) for v
can be
computed in O(E) for v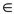 V.
V.
c)
wi can be defined as 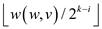 .Here, it
is enough to show that either
.Here, it
is enough to show that either 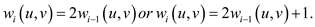
To Prove:
 . The weight of the shortest path is given below:
. The weight of the shortest path is given below:
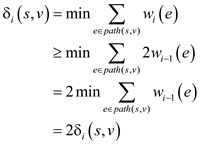
Similarly,
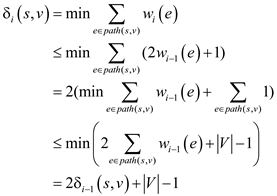
d)
Proof:

Therefore, wi can never be negative.
This can be proved as shown below:

The terms 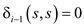 because the
path from a node to itself is zero, and the minimum path length
from s to v using wi function is
because the
path from a node to itself is zero, and the minimum path length
from s to v using wi function is  .
.
Therefore, from (c) it can be proved that  .
.

f)
If  is known
then
is known
then  can be
computed by using the equation in part (d) in time O(E).
can be
computed by using the equation in part (d) in time O(E).
For each edge calculate wi(u,v)
From part (e) it is clearly shown that  is bounded
by |E|.
is bounded
by |E|.
By using part (a) we can compute the shortest path distance
 in
time O(E).
in
time O(E).
By using part (e) compute the shortest path distance  in tine O(V)
for each vertex.
in tine O(V)
for each vertex.
Therefore, 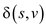 can be
calculated in time O(E lg W). From (b) it is shown that
can be
calculated in time O(E lg W). From (b) it is shown that  in time
O(E).
in time
O(E).
Calculate  from
from
 in
time O(E) up till
in
time O(E) up till  . Here,
k=O(lg W), the running time of the algorithm is O(E lg W).
. Here,
k=O(lg W), the running time of the algorithm is O(E lg W).
Bitonic shortest paths
There can be a maximum of two changes in direction for bitonic sequence. That is bitonic sequence can increase, and then decrease and then increase or bitonic sequence can decrease, then increase and then decrease. Before going to solve complex bitonic problem let’s make simple changes to the given problem.
Suppose instead of given condition of bitonic sequence, consider
a condition like for each vertex v, where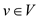 , the
weights of edges along any shortest path from s to v
are increasing.
, the
weights of edges along any shortest path from s to v
are increasing.
For example consider the weighted graph shown below,
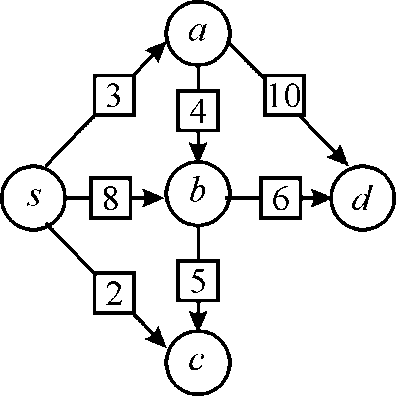
Here there are two shortest paths from s to d.
There are 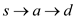 and
and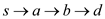 . These
shortest paths are in increasing order. Now to sort edges in the
increasing order, call INITIALIZE-SINGLE-SORCE and then relax all
edges one at a time. Then edges that are along every shortest path
are relaxed.
. These
shortest paths are in increasing order. Now to sort edges in the
increasing order, call INITIALIZE-SINGLE-SORCE and then relax all
edges one at a time. Then edges that are along every shortest path
are relaxed.
For example,
In the given graph, the edges are added in the order (2, 3, 4,
5, 6, 8, and 10). Then both shortest paths 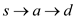 and
and
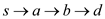 will be covered in single pass.
will be covered in single pass.
Now consider the condition like weights of edges along shortest paths increases and then decreases as shown in graph below.
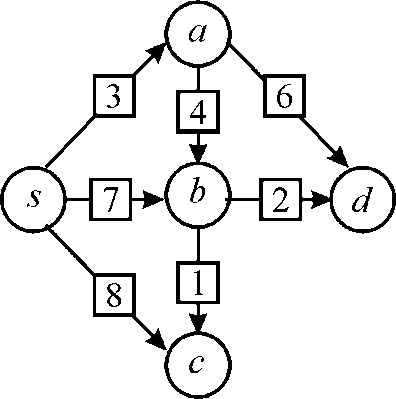
Now if the edge is relaxed again increasing order of edges then
the starting edge would be edge 1 and it cannot be added to
shortest path because its weight remains . Next edge
2 also cannot be added. Now edge 3 onwards could be added. So in
the computed shortest path only the path
. Next edge
2 also cannot be added. Now edge 3 onwards could be added. So in
the computed shortest path only the path  will be
there.
will be
there.
Now if the edge is relaxed again in decreasing order then both 2
and 1 will be added and one shortest path is achieved and that is
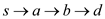 .
.
From the two examples above, to handle increasing sequence, only one pass is needed. To handle an increasing and decreasing sequence, it requires two passes.
So in the case of bitonic sequence to cover all the shortest paths, four passes are needed, in which pass one and three will be in increasing order of edge weight and pass two and four will be in decreasing order of edge weight.
For example see the graph given below,
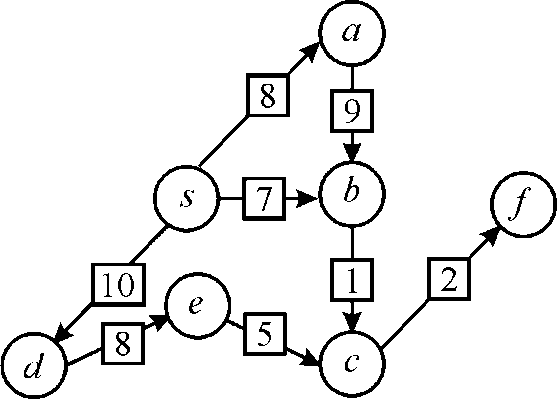
Here there are two shortest paths from s to f
having equal weights. They are 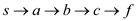 which are an
increasing, then decreasing and then increasing. Bitonic sequence
(8, 9, 1, 2) and
which are an
increasing, then decreasing and then increasing. Bitonic sequence
(8, 9, 1, 2) and 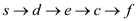 which is
decreasing, then increasing and then decreasing bitonic.
which is
decreasing, then increasing and then decreasing bitonic.
In pass one (increasing order) edges having weights (7, 8, 9, and 10) will be added. In pass 2 (decreasing order) edges 3 will be added and so on.
So, the algorithm for, two given conditions
1: Edge weights are in bitonic sequence.
2: Edge weights are unique is given below.
Algorithm:
BITONIC SHORTEST PATH 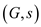
SORT (E)
INITIALIZE-SINGLE-SOURCE
for each edge (u, v) in E in increasing order
do
relax (u, v, w)
for each edge (u, v) in E in decreasing order
do
relax (u, v, w)
for each edge (u, v) in E in increasing order
do
relax (u, v, w)
for each edge (u, v) in E in decreasing order
do
relax (u, v, w)
Analysis of above algorithm:
Time to sort 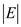 edge by
weight is
edge by
weight is 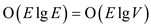 because
because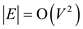 .
INITIALIZE-SINGLE_SOURCE will take
.
INITIALIZE-SINGLE_SOURCE will take 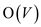 time.
time.
Each pass will take 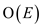 time.
time.
So, total time for BITONIC SHORTEST PATH 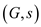 is
is
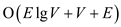 =
=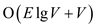 .
.