Equivalent network on splitting an edge:
Consider the flow network 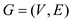 , which
contains an edge (u, v).
, which
contains an edge (u, v).
Now, create a new network  from graph
G by splitting the edge (u, v) into two edges by
adding a vertex x between vertex u and vertex
v and assign
from graph
G by splitting the edge (u, v) into two edges by
adding a vertex x between vertex u and vertex
v and assign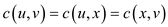 . .
Where
. .
Where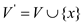 and
and
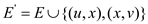 .
.
Now, the resulting network  is
equivalent to the graph G, because the net flow at u and
v in
is
equivalent to the graph G, because the net flow at u and
v in  are the
same as in G. That is, the outflow and inflow at u
and v are same in
are the
same as in G. That is, the outflow and inflow at u
and v are same in  and
G , since the cost of the new edges is equal to the cost of
(u,v).
and
G , since the cost of the new edges is equal to the cost of
(u,v).
Therefore,the network  created from
a graph G by splitting an edge in G is
equivalent to the original network G.
created from
a graph G by splitting an edge in G is
equivalent to the original network G.
Maximum flow:
Since the flow at new edges is same as the flow at original edge
(u,v), the maximum flow in  does not
change. That is, the maximum flow in
does not
change. That is, the maximum flow in  is same as
the maximum flow in G.
is same as
the maximum flow in G.
Hence, on forming a new network by splitting an edge in a network into the two edges with same capacity, the flow of the network remains same and the two networks are equivalent.
Example:
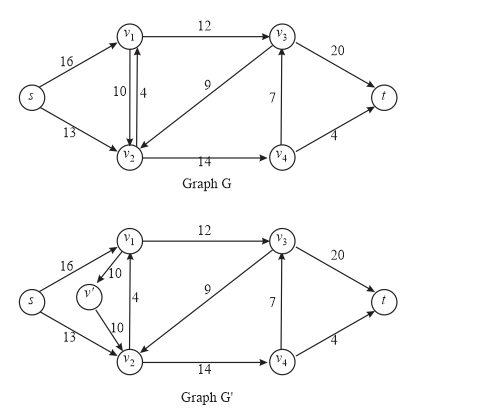
Fig: splitting of edge in flow network
A flow in a graph G with vertices V, a source vertex s,
and sink vertex t is defined as a real-valued function
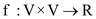 satisfies
the given two properties:
satisfies
the given two properties:
Capacity constraint: For all 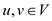 , require
, require
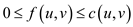 .
.
Flow conservation: For all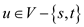 ,
require
,
require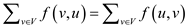 .
.
For a graph G with multiple-source vertices 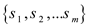 and
multiple-sink vertices
and
multiple-sink vertices 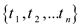 the flow
properties to determine the maximum flow is shown below:
the flow
properties to determine the maximum flow is shown below:
1. The maximum flow value in the single source and single sink network is identical to the maximum flow value in the multiple-source and multiple-sink network.
2. The maximum flow can be easily determined by converting the multiple-source and multiple-sink network into the single source and single sink network.
Let the source vertex be  and the
sink vertex be
and the
sink vertex be  and satisfy
the “flow in, flow out” constraint. Let the value of a flow in
multiple source, multiple sink problem be
and satisfy
the “flow in, flow out” constraint. Let the value of a flow in
multiple source, multiple sink problem be  and set
and set
 .
This will satisfy both the properties that is capacity constraint
and flow conservation constraint. In single source, no edges come
into s. So, flow is
.
This will satisfy both the properties that is capacity constraint
and flow conservation constraint. In single source, no edges come
into s. So, flow is  and it is
equivalent.
and it is
equivalent.
Flow network 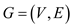 is a network
in which each edge has a non-negative capacity
is a network
in which each edge has a non-negative capacity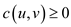 .
.
Let V1 be the set of vertices. For every vertex v in network, there exist a path such that
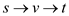 …… (1)
…… (1)
Where s is the source vertex and t is the sink vertex.
• Assume u be the vertex for which equation (1) doesn’t hold. This implies that there is no flow exists between u to v.
So,
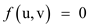 …… (2)
…… (2)
• Since for all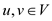 , there
exists a capacity constraint
, there
exists a capacity constraint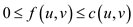
If 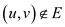 and
and
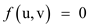 then by flow conservation rule,
then by flow conservation rule,

• Since from equation (2) the value of 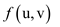 is 0,
is 0,
So,
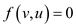 …… (3)
…… (3)
Hence from equation (2) and (3) 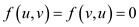
• Now Source is the vertex from which only flow is outgoing and
sink is the vertex which only is receives the flow. Since after
giving the flow 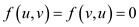 to
u, the flow property doesn’t violate because the capacity
for any edge is a non-negative integer and flow should always be
less than or equal to the capacity which is true in this case.
to
u, the flow property doesn’t violate because the capacity
for any edge is a non-negative integer and flow should always be
less than or equal to the capacity which is true in this case.
Hence there must exist a maximum flow f
in G such that 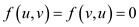 for
all vertices
for
all vertices 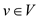 , if
there is no path from source( s ) to
u and u to sink (
t ).
, if
there is no path from source( s ) to
u and u to sink (
t ).
Flow: The flow between two vertices is a real valued
function. It is denoted by .
.
The scalar flow product is denoted by 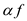 and defined
as follows:
and defined
as follows:
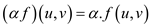
Convex Set: Convex Set comprises a set of points in which the line formed by any two points always falls within the set. In other words, this means that the points in the set form a connected component.
To prove that the flows in a network form a convex set, it is to
be shown that if  and
and
 are flows, then
are flows, then 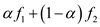 is also a
flow for
is also a
flow for 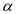 in the
range
in the
range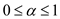 .
.
The total flow between two vertices which is denoted by
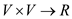 has to satisfy these three properties:
has to satisfy these three properties:
• Capacity constraint
• Skew symmetry
• Flow conversation
1. Capacity Constraint: It states that the flow in an edge cannot exceed its capacity.
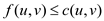
It is given that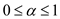 .
.
So, it is inferred that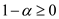 .
.
Thus, for any edge , the
following can be observed:
, the
following can be observed:

Since, the flow in any edge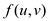 cannot
exceed its capacity
cannot
exceed its capacity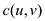 .
.
So, both 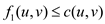 and
and
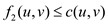
Thus, for this instance of the flow, it becomes the following:
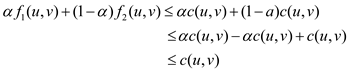
So, it is found that 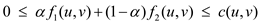
Hence, the capacity constraint property is satisfied.
2. Skew Symmetry: It states that the flow in an edge is symmetric on both sides. That is the flow from one vertex to another is the same as the flow in the opposite direction.
For ,
, 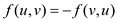
So, for this instance of the flow, both 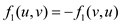 and
and
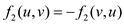 must hold.
must hold.
Thus, for any edge , the
following is observed:
, the
following is observed:

From the above, it is seen that 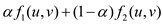 abides by
the skew symmetry property.
abides by
the skew symmetry property.
Thus, it is concluded that the skew symmetry property is satisfied.
3. Flow Conservation: It states that except the source
and the sink nodes which are denoted by 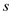 and
and
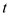 respectively, the net flow entering a node
respectively, the net flow entering a node  is 0.
is 0.
For all  .
.
Since,  and
and
 are
flows. They satisfy the flow conservation. So, the following is
observed for these two flows:
are
flows. They satisfy the flow conservation. So, the following is
observed for these two flows:
 and
and  …………. Eqn.
(1)
…………. Eqn.
(1)
Thus, for this instance of the flow, the net flow at a node except source and sink is the following:
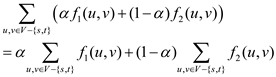
Putting equation (1) in the above equation:

Hence, the net flow in this case is also 0 and thus, property of flow conservation is satisfied.
Since, it is shown in the previous steps that the flow 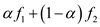 exhibits
all the three properties namely, capacity constraint, skew symmetry
and flow conservation.
exhibits
all the three properties namely, capacity constraint, skew symmetry
and flow conservation.
Hence, it is proved that if  and
and  are
flows, then
are
flows, then 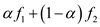 is
also a flow for all
is
also a flow for all 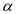 in
the range
in
the range 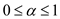 .
.
Consider a graph  and the
max-flow problem over the taken graph with the specified
capacities
and the
max-flow problem over the taken graph with the specified
capacities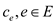 .
.
Suppose, R represent the value of the s (source node) – t (terminal node) flow, where, R needs to be maximized.
The representation of max-flow problem is given below:

And,

And,
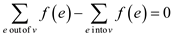 , for
, for
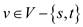 and
and
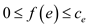 for
for
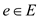
In this optimization, the decision variables which need to be
calculated are the flow value R and the flow
variables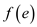 ,
, 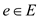 .
.
From, the above it is clearly seen that this is a linear program
in the decision variables. Consider the following rewritten linear
programming in the matrix form. Here, two vectors 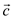 and
and
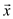 are
defined as follows:
are
defined as follows:

And
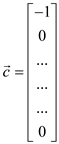
Therefore, the max-flow LP problem reduces to minimized
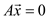
 for
for
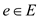
Where, x denotes the length 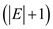 of the
vector. The component, which is used first in the x, denotes
the rate variable and the other remaining variables denotes the
flows over the edges.
of the
vector. The component, which is used first in the x, denotes
the rate variable and the other remaining variables denotes the
flows over the edges.
The dimension of the matrix A is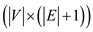 . Then, the
matrix A can be represented as
. Then, the
matrix A can be represented as , where,
, where,
 denotes the
flow vector multiplication matrix and
denotes the
flow vector multiplication matrix and  denotes the
column vector multiplying the variable R.
denotes the
column vector multiplying the variable R.
• The matrix  is the
node-arc incidence matrix of the taken graph G. The column
of the matrix corresponds to an edge
is the
node-arc incidence matrix of the taken graph G. The column
of the matrix corresponds to an edge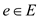 .
.
• If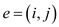 , then
, then
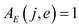 and
and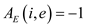 . Similarly,
. Similarly,
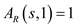 and
and
Consider a flow network G = (V, E) in which vertices v of the network has capacity limit l(v) of the flow that can be flowed from the network in addition to edge capacity. Now we have to transform this network into G’ = (V’, E’) without vertex capacities so that the flow in the network G is equivalent to the flow in the network G’.
Flow network is the network which shows the automation of assembly line in the company from the warehouse to the manufacturing location and vice versa. In this network the raw material passes through various stages to be a finished product.
Maximum flow is the rate at which the data flows from the source vertex to the sink vertex or it is the rate of flow of data through the network.
For the graph G = (V, E) with flow limits l(v) for the vertex v, a method to find the graph G' without the flow limit on the vertices is: “the addition of one more vertex, such that the edge connecting the new and the old vertex is the limit of the vertex in the previous stage.”
For example: Consider graph G
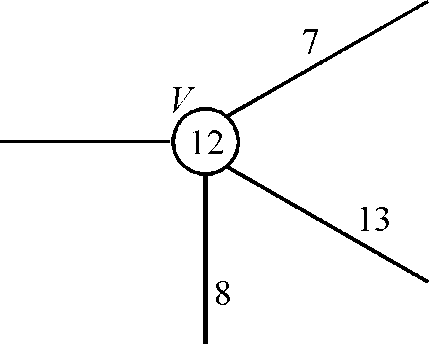
In this graph the limit of the vertex V is 12 and we have to transform this vertex in the graph without vertex limit then we create a new vertex
The resulting figure G’ would be:
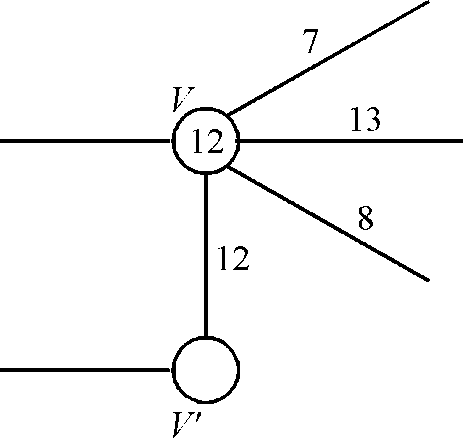
Here for every vertex other than the source and sink, we will have to add another vertex that is (V-2) more vertices are added and with each new added vertex one edge associated so (V-2) new edges are also added.
So the total number of vertices in the graph is:
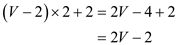
Number of vertices 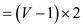
Number of edges =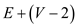 .
.
Hence, after the conversion of a graph G with vertex
capacities into the graph G’ with no vertex capacities, the
total number of vertices in graph G’ are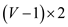 and total
number of edges are
and total
number of edges are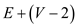 .
.
