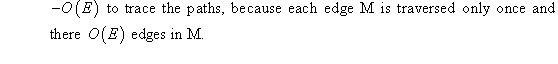a)
Consider a network flow G = (V, E) with edge capacity
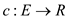 and vertex capacity
and vertex capacity 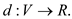
Keep the edge capacity constraint, skew symmetry and flow conservation same.
Consider the new requirement: for every 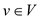 there is a
need for
there is a
need for 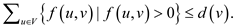
Consider, G’= (V’, E’) with only edge capacity be a new flow network. The maximum flow in G is equal to a maximum flow in G’ and vice-versa.
G’ is the edge capacity given by .
.
To construct G’ from G, it is necessary to
splitting every vertex 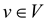 into two
vertices vin and vout.
into two
vertices vin and vout.
After splitting, insert a new edge (vin, vout) with capacity c’(vin, vout) = d(v) between the two parts of the split vertex.
From the above constraints,
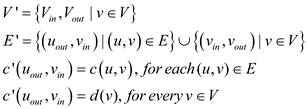
Let, ‘s’ and ‘t’ be the source and the sink vertex in G respectively, the source vertex and the sink vertex in G’ is sin and tout.
In order to reduce the escape problem, let there be n starting points on the grid and 4m-4 boundary points. Now, construct G= (V, E) considering the below points:
• Assume s as a temporal source vertex and connect it to each of the n starting points.
• Assume t as a temporal sink vertex and connect it to each of the 4m-4 boundary points to t.
• Each undirected edge between point’s u and v in the original grid is changed into directed edges (u, v) and (v, u) in G.
• The edge capacity is assigned to 1 to each vertex in G.
b)
Efficient algorithm to solve the escape problem running time:
• Number of points in the input grid has = n2 points
• Number of undirected edges = 2n2 -2n
• Therefore, G has 2+n2 = O(n2) vertices and m+(4n2-4)+2(2n2-2n)=m+8n2-4n-4 =O(n2) edges.
• Hence, the running time is O(n2).
• By applying ford-Fulkerson method on G’ the cost is O(E’.|f*|) = O((E+V).|f*|), here f* is maximum.
• In this case, |F*|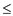 4n-4 and
|E|+|V|=O(n2).
4n-4 and
|E|+|V|=O(n2).
• Therefore, for higher bound running time is O((E+V).|f*|=O(n3)
Flow Network
A flow network, in the most basic form, is a directed graph. Each of the edges has a capacity assigned to it. In the network a certain amount of flow goes from each edge of the network. There are certain nodes in the graph from which the flow starts and to which the flow ends. These two nodesare known as the sourceand sink of the network respectively.
In the diagram below the node s is the source of the network and the node t is the destination or sink of the network. Each of the graph edge has a capacity. The capacity defines the data value that can go through that edge. The capacity is always a positive integer. One more thing is that if there existsan edge from a vertex v1 to vertex v2 than there can be no edge from v2 to v1.
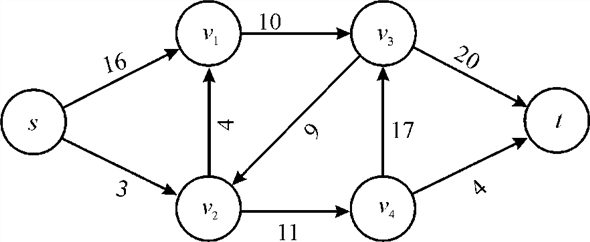
In the above diagram the vertex s is called the source of the network and the vertex t is called the sink or destination of network. The capacity of each edge is shown alongside the edge. As the edge from s to v1 has the capacity of 16. A flow network has various applications in practicality. It is used in data warehouses, scientific research and electricity distribution etc.
Algorithm consulting: Consider that in an algorithm
consulting company there are n important subareas of
algorithms. For a particular area  of
algorithms the
of
algorithms the dollars are
being paid to hire an expert. The company has lined up of potential
job. To perform a job, experts are hired from the subsets of
subareas. These experts can work on multiple jobs at a time. It
gives the company the revenue in dollars (pi).
The area in which the hiring of algorithm experts is required is
as:
dollars are
being paid to hire an expert. The company has lined up of potential
job. To perform a job, experts are hired from the subsets of
subareas. These experts can work on multiple jobs at a time. It
gives the company the revenue in dollars (pi).
The area in which the hiring of algorithm experts is required is
as:

The potential jobs set that are defined by the hiring company as:

The company’s target is to maximize the revenue. The maximum net revenue of the company is calculated by subtracting the cost incurred in the employing the experts from the total income of accepted jobs.
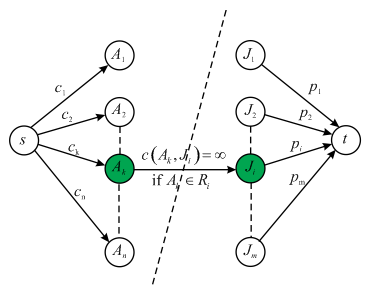
A flow network G for algorithm
consulting: The flow network created for the algorithm company
has a source network s, vertices , vertices
, vertices
 and a sink vertex t. The edges of this network are defined
as:
and a sink vertex t. The edges of this network are defined
as:
For  there is an
edge
there is an
edge  with
capacity
with
capacity  as shown
below:
as shown
below:

For there is as
edge
there is as
edge  which has
the capacity
which has
the capacity  as
shown:
as
shown:

There is one more condition in the flow network that is
 and
and if
the vertex
if
the vertex  then there
is an edge from vertex
then there
is an edge from vertex 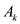 to
vertex
to
vertex which has
infinite capacity.
which has
infinite capacity.
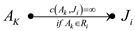
The flow network created from the above description is as:
a. Suppose that for a finite capacity-cut, one of
the vertices is on the S side. S side refers to the
vertex partitions in which source s is present. Now, if a
vertex is present on the S side, then the edge connecting
 with the
vertex
with the
vertex  will be
counted when calculating the value of the cut. To recall, it can be
stated that a cut involves the sum of edges between vertices of
S and T (corresponding to sink). The capacity of the
cut (S, T) is:
will be
counted when calculating the value of the cut. To recall, it can be
stated that a cut involves the sum of edges between vertices of
S and T (corresponding to sink). The capacity of the
cut (S, T) is:

Now, since the vertex will be on S side and the edge will
be counted, the capacity cannot be finite, since the edge weight is
not finite for the connection of 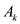 with
with .
.
Other approach-Proof by contradiction: For the
contradictory proof consider that in a graph having finite capacity
cut (S, T) it is true that for the
vertices
for the
vertices .
.
Now, if  then it must
be in the set of S that is
then it must
be in the set of S that is .
.
Now, it is known that . So, the
cut (S, T) will be on the edge
. So, the
cut (S, T) will be on the edge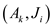 in the
network G as shown in the figure:
in the
network G as shown in the figure:
From the graph it is clear that the capacity of the edge
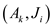 is
is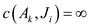 . So, the
capacity of cut (S, T) will be infinite. The assumption is
contradicted here. Hence, the cut (S, T) will be of finite
capacity cut if
. So, the
capacity of cut (S, T) will be infinite. The assumption is
contradicted here. Hence, the cut (S, T) will be of finite
capacity cut if  for
for .
.
b . Consider a flow network graph G (V, E) with the capacity c(u, v) from node u to v having source s and sink t. For maximum amount of flow, this is sentfrom s to t through the network.
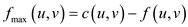
Now, considering the above expression of maximum flow, the problem can be modeled as a flow graph. In the model M of problem there will be two attributes first is the set of accepted jobs M.J and the other denotes the set of experts hired M.A. The model for the problem will be valid only if all the hired experts are required for the jobs.
Consider M as a valid project plan that is in this
project plan the requirement for the experts is fulfilled. Now, if
 is
the accepted job set that is
is
the accepted job set that is 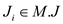 then for
each
then for
each , the expert
, the expert
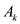 will be the
part of hired experts that is
will be the
part of hired experts that is .
.
The edges from s to 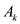 is
representing the cost
is
representing the cost and the
edges from vertices
and the
edges from vertices  to sink
t would represent income, that is:
to sink
t would represent income, that is:

The maximum net revenue of the company is calculated by subtracting the cost incurred in the employing the experts from the total income of accepted jobs. For finding the project plan with maximum net revenue the lemma will be used which is setting up the relationship between the minimum cut capacity and the valid project plan revenue.
Lemma: In a flow network G, for a minimum cut
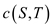 of
finite capacity there must be a valid model of project having total
of
finite capacity there must be a valid model of project having total
 revenue.
revenue.
The proof of lemma will be done in two parts in the first part the project model will be created for a network having a finite capacity cut. While in the other part the minimum cut of finite capacity for a valid project model will be created.
Now, for the first side consider that (S, T) is a minimum
cut of finite capacity 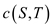 in a flow
network G. Creating the project model M for this
graph which contains the job set
in a flow
network G. Creating the project model M for this
graph which contains the job set  in the
attribute M.J in the condition when
in the
attribute M.J in the condition when  . It also
includes the expert
. It also
includes the expert 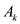 in the
attribute M.A for
in the
attribute M.A for . As it is
proved in the previous part that the project model M is
valid because for each
. As it is
proved in the previous part that the project model M is
valid because for each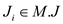 it is true
that
it is true
that if and only
if
if and only
if .
.
It is assumed that the cut(S, T) is of finite
capacity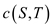 , so there
will not be any edge
, so there
will not be any edge 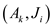 which
crosses the cut for
which
crosses the cut for and
and . In the
finite cut (S, T) the edges joining the vertices of
set S to set T must be either in the form of
. In the
finite cut (S, T) the edges joining the vertices of
set S to set T must be either in the form of or
or .
.
Now, suppose that 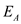 and
and are edges
set of the form
are edges
set of the form and
and respectively and these edges are crossing the cut. So the capacity
of cut:
respectively and these edges are crossing the cut. So the capacity
of cut:
 … … (1)
… … (1)
Consider that is possible
only when
is possible
only when which is
possible if
which is
possible if  and from
the graph G,
and from
the graph G,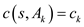 .
.
So,

Similarly for the edges of the form  the
possibility that
the
possibility that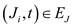 is true
only when
is true
only when  it
means
it
means which in
turn proves that
which in
turn proves that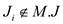 . From the
constructed graph G the capacity of edge
. From the
constructed graph G the capacity of edge  is
is that is
that is
 .So,
.So,

Suppose that r is the total revenue of the project model M then from the definition of revenue:


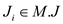 assume
that
assume
that and for each
expert
and for each
expert  assume
that
assume
that .For the
proof of cut (S, T) to be of finite capacity,
consider that the edges
.For the
proof of cut (S, T) to be of finite capacity,
consider that the edges  are the only
edges having infinite capacity. It is considered that there are no
edges
are the only
edges having infinite capacity. It is considered that there are no
edges  such
that
such
that and
and are present
in the graph. So, the capacity of minimum cut is finite.
are present
in the graph. So, the capacity of minimum cut is finite. and
and there is an
edge
there is an
edge . From the
project model the job set
. From the
project model the job set 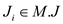 and the
expert
and the
expert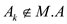 . But for
the edge
. But for
the edge  it is clear
that
it is clear
that . Since
M is valid project model so, the expert
. Since
M is valid project model so, the expert . For the
calculation of total revenue of project model the analysis is as
above that is the total revenue.
. For the
calculation of total revenue of project model the analysis is as
above that is the total revenue. 

c. Consider the graph G drawn above containing the source s and sink t and the edges
 Having capacity
Having capacity  which
represents the cost of hiring expert
which
represents the cost of hiring expert 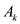 and the
edges
and the
edges having
capacity
having
capacity ,
representing the revenue for job plan
,
representing the revenue for job plan .
.
For finding the right job selection and the eligible expert for that job first of all finding the maximum flow in the created flow graph. After that minimum cut set is discovered by using the depth first search algorithm. If any expert who belong to the minimum cut set but is not hired yet then hire that expert. Similarly if a job doesn’t belong to the minimum cut then accept that job.
The algorithm for the selection of right job and expert can be written as follows:
1. Find the maximum flow and the residual network for the graph.
2. Find the minimum cut set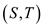 using the
depth first search (DFS) traversal.
using the
depth first search (DFS) traversal.
// check if the edge belongs to the minimum cut.
3. if E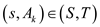
4. Hire the expert
// check if the edge do not belong to minimum cut.
5. if E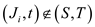
6. Accept the job
7. end
The DFS method used in the above algorithm is as follows: The depth first search is a searching method which starts its process of searching from the root node and explores all the nodes till the end before returning back. The depth first search algorithm initially all the nodes are painted with white color and the parent of each node is set to NIL. The initial time to visit the node is also set to zero. After that each white node is explored and the status is updated by calling the process DFS-VISIT.
DFS ( G )
// run the loop for each vertex of graph
1. for each vertex 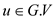
// assign the color to each node
2. u.color= white
// store nil in the parent field of each node
3. 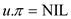
// initial time of discovering the node
4. time = 0
// execute loop once for each node
5. for each vertex 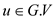
// check if the color of the node is “white”
6. if u.color = white
// call the method to discover the node
7. DFS-VISIT (G, u)
So the above two “if” conditions give the accepted jobs
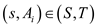
And the hired expert
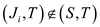
Analysis of algorithm: The total complexity of the algorithm would depend on the implementation of the maximum flow algorithm. Here, n and m refer to the range of value of i and k used in the algorithm stated above. Above algorithm set has length of n and potential job associated with these subareas have length m.
So, total option comes out to be mn. And this is the
worst case because here consideration is up-to last option.
Finally, for hiring the expert, again set A comes in the
picture which has length n. Now, taking all considerations
which are mentioned above gives the final running time
of . This
is the extreme case, and it will not exceed the range. So, this is
an optimal and efficient approach. Hence, the total time of
execution of the algorithm which selects which expert to hire and
which job to choose would be
. This
is the extreme case, and it will not exceed the range. So, this is
an optimal and efficient approach. Hence, the total time of
execution of the algorithm which selects which expert to hire and
which job to choose would be .
.
Flow Network
A flow network, in the most basic form, is a directed graph. Each of the edges has a capacity assigned to it. In the network, a certain amount of flow goes from each edge of the network. There are certain nodes in the graph from which the flow starts and where the flow ends. These two nodes are known as the origin and destination of the network respectively.
In the diagram below, the node s is the origin of the
network and the node t is the destination or sink of the
network. Each of the graph edge has a capacity. The capacity
defines the data value that can go through that edge. The capacity
is always a positive integer. If there exists an edge from a vertex
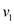 to
vertex
to
vertex 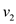 , than there
is an edge from v2 to v1.
, than there
is an edge from v2 to v1.

In the above diagram, the vertex s is called the origin of the network and the vertex t is called the sink or destination of network. The flow limit of each edge is shown alongside the edge. As in the graph, the flow limit of edge s to v1 is 16. The flow for an edge is defined as the amount passed from a vertex to the other vertex. For any edge of the network, the total value of flow is either smaller than or equal to the flow limit of concerned edge. The total flow is the total amount being passed through the network.
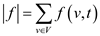
Maximum flow: For a flow network, maximum flow is defined as the largest quantity of flow that could pass from the origin vertex to the destination.
Cut and minimum cut: For a flow network, the cut
(S, T) is the division of the vertices of the network
into two groups S and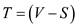 such that
the source vertex s is contained in set S and the
sink vertex t is contained in set T.
such that
the source vertex s is contained in set S and the
sink vertex t is contained in set T.
The flow value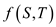 of the cut
is defined as the sum of flow of every edge
of the cut
is defined as the sum of flow of every edge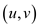 for
which
for
which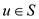 and
and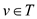 . It means
that the total flow of a cut is the total of the flow of edges from
S side to T side. The formula of calculation of flow
of cut is as follows:
. It means
that the total flow of a cut is the total of the flow of edges from
S side to T side. The formula of calculation of flow
of cut is as follows:
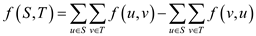
The limit of flow of the cut in a flow network is the sum total of the capacities of the edges involved in the cut. The formula for the cut capacity is,

Minimum cut is that cut of the flow network for which the sum of capacity of cut edges is minimum.
Maximum flow by scaling: Consider that 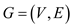 as a flow
network. Source (it is considered as the origin of flow) as
as a flow
network. Source (it is considered as the origin of flow) as
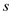 and
sink (it is considered as the end point, that is, the point where
flow gets accumulated at the end) as
and
sink (it is considered as the end point, that is, the point where
flow gets accumulated at the end) as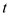 . Each edge,
say
. Each edge,
say 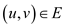
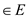 , has some
integer capacity denoted by
, has some
integer capacity denoted by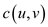 .
. 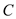 is defined
as
is defined
as .
.
a. Minimum cut of a graph G is that for which the total sum of capacity of edges involved in the cut set in is minimum. That is, the edges are selected in such a way that their sum is minimum.
As in the graph G there are E edges, therefore
maximum number of edges that are leaving 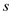 and entering
and entering
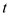 cannot be greater than
cannot be greater than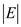 .Since,
C is defined as
.Since,
C is defined as , is the
largest possible flow limit of any edge in the network therefore
the flow limit of edges can be more than C.
, is the
largest possible flow limit of any edge in the network therefore
the flow limit of edges can be more than C.
Now, if the cut(S, T) is lowest capacity cut of the network is crossing all the edges then the capacity of cut;
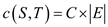
Therefore, maximum flow of graph can be at most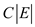 .Hence, by
max-flow min-cut theorem, the minimum cut of graph G can
have greatest value of capacity
.Hence, by
max-flow min-cut theorem, the minimum cut of graph G can
have greatest value of capacity 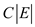 .
.
An augmenting path of a Graph G is a simple path in a graph starting from source s and ending at sink t which has a non-negative capacity. Hence, if there is a possibility of an augmenting path, the flow of a graph is not a max-flow. Thus, it can be concluded that flow of a graph is a max flow if no augmenting path is possible in the flow network. The capacity of any augmenting path is always equal to the flow limit of that edge which has minimum flow limit in the augmenting path.
For example: Suppose that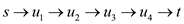 is an
augmenting path in the flow network. Then its capacity can be
calculated by the edge belonging to the path with minimum capacity.
For finding out an augmenting path of capacity not less than
K, search for those edges having capacity at least K.
If there is any edge in the graph which has capacity less than
K then ignore that edge.
is an
augmenting path in the flow network. Then its capacity can be
calculated by the edge belonging to the path with minimum capacity.
For finding out an augmenting path of capacity not less than
K, search for those edges having capacity at least K.
If there is any edge in the graph which has capacity less than
K then ignore that edge.
Breadth first search will be applied to find a path by
considering only those edges having residual capacity at least
K. Breadth first search is the method of searching in a
graph. In this method, each node of the graph is explored in a
sequential order. The time taken by breadth first search for a
graph having V vertices and E edges is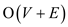 . Since for
a flow network,
. Since for
a flow network, 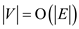 , therefore
total time is
, therefore
total time is 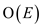 .
.
Hence, breadth first search is an efficient way to search for an
augmenting path which has minimum capacity K, and it takes
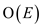 time.
time.
c.
As in the MAX-FLOW-BY-SCALING method, the search for the path
having capacity from  down to 1 is
done. If such path, with an augmenting path having capacity greater
than 1 is found, then the flow is augmented with that path.
down to 1 is
done. If such path, with an augmenting path having capacity greater
than 1 is found, then the flow is augmented with that path.
This is the same concept as in FORD-FULKERSON method, so it is clear that the MAX-FLOW-BY-SCALING algorithm uses FORD-FULKERSON method. It is true that the flow value in a network will always be an integer. Thus, the capacity of augmenting path is a positive value, and hence, the augmenting path is not found in the residual network. Therefore, MAX-FLOW-BY-SCALING method always returns a largest value of flow.
Illustration of MAX-FLOW-BY-SCALING algorithm:
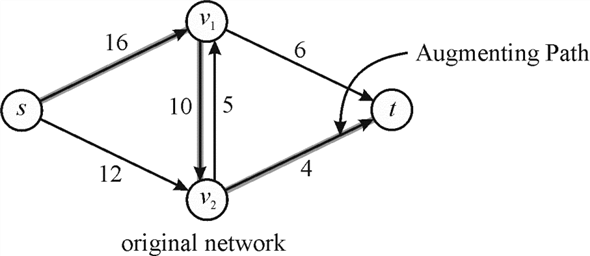
1. The graph below shows the flow network in which the dark black continuous show an augmenting path of minimum capacity 4.
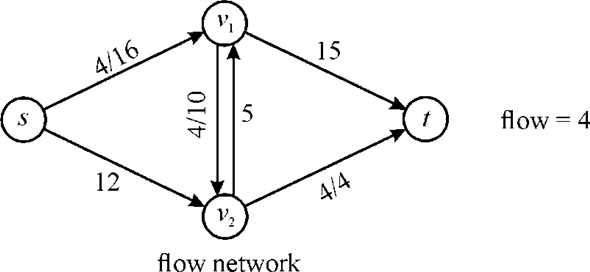
2. Pass the flow equivalent to the flow limit of the augmenting path through the path and update the flow value as shown in the graph below:
3. Now, the residual network of flow graph again shows an augmenting path of the network with minimum capacity 6.
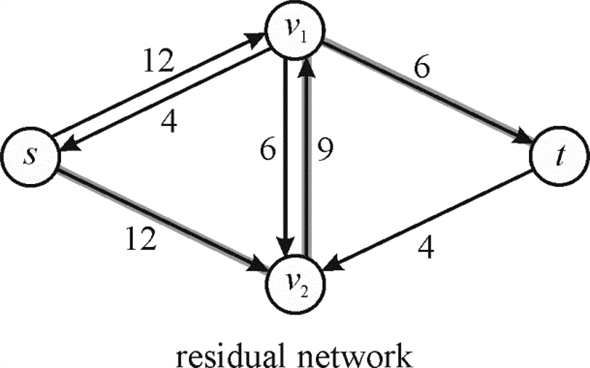
4. Again, pass the flow through the path equal to the minimum capacity of augmenting path.
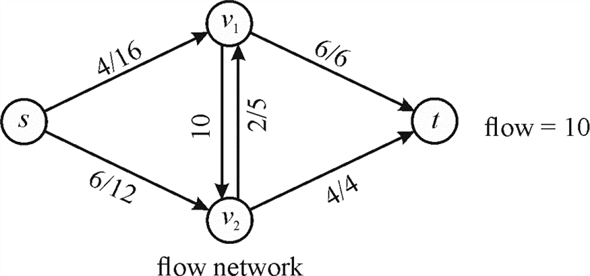
Now, as the edges towards sink t are saturating edges with no more flow that can be passed through them, the greatest value of flow in the network is 10. Hence, the algorithm MAX-FLOW-BY-SCALING returns the largest value of flow in the network.
As there are E edges in the graph and each time line 4 is
executed, the greatest flow limit of the residual network  can be
2K. This is because, in a flow network, flow between edges
has two phases. One is sink and the other is source, and the
maximum capacity of a flow is K. Thus, the final outcome is
2K.
can be
2K. This is because, in a flow network, flow between edges
has two phases. One is sink and the other is source, and the
maximum capacity of a flow is K. Thus, the final outcome is
2K.
In (b) part, it has been shown that there
is an augmenting path of capacity at least K in  time. Here,
the change is in the value of K. Thus, minimum cut of the
residual network Gf can have the capacity at most
time. Here,
the change is in the value of K. Thus, minimum cut of the
residual network Gf can have the capacity at most
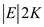 ,
that is,
,
that is, 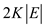 .
.
e.
As in the part d, it is been calculated that for
residual network 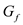 , the flow
limit of the cut with lowest capacity cannot be greater than
, the flow
limit of the cut with lowest capacity cannot be greater than
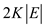 whenever the
line 4 of the algorithm MAX-FLOW-BY-SCALING executes. The value of
largest flow in the network G is the sum of the flow value
in the network G and the largest flow value in the residual
network of G. That is,
whenever the
line 4 of the algorithm MAX-FLOW-BY-SCALING executes. The value of
largest flow in the network G is the sum of the flow value
in the network G and the largest flow value in the residual
network of G. That is,

Here, f is the flow in network G, and f’ is
the flow in residual network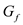 . By max
flow min-cut theorem, the maximum flow of
. By max
flow min-cut theorem, the maximum flow of 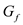 is at
most
is at
most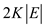 .
.
Now, by definition, each time line 5 is executed, K
capacity is calculated of augmented path, which is capacity of
residual network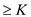 . Therefore,
for each value of K, loop of lines 5-6 runs at most
. Therefore,
for each value of K, loop of lines 5-6 runs at most
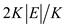 times, that is,
times, that is, 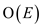 times.
times.
f.
The total running time of MAX-FLOW-BY-SCALING algorithm depends on the following 3 factors:
1. Execution time of while loop in line 4.
2. Execution time to find an augmenting path of capacity at
least 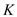 of line
5.
of line
5.
3. Execution time of while loop of line 5 for each
fixed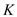 .
.
1. Initially, . Each time
value of
. Each time
value of 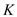 is reduced
to half of its original value that is
is reduced
to half of its original value that is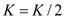 . It can be
said that above sequence is a geometric progression (GP)
with ratio being ½. Now, minimum value of
. It can be
said that above sequence is a geometric progression (GP)
with ratio being ½. Now, minimum value of 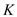 is 1, that
is,
is 1, that
is,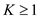 . Thus, the
sequence is as follows:
. Thus, the
sequence is as follows:
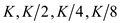 … … (1)
… … (1)
Now, calculate number of terms that will be equal to the number of times loop is running. By definition of GP,
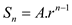
Here,
 =
=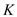
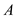 =1
=1
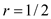
Thus,

Substitute the value of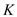 .
.
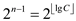
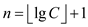
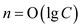
2. By part b, for a given 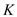 , to find an
augmenting path of capacity at least
, to find an
augmenting path of capacity at least 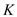 , will
take
, will
take
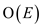 time.
time.
3. By part e, for each value of 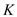 , while loop
of line 5 will take
, while loop
of line 5 will take 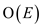 time.
time.
Combine the time calculated from equations (1), (2) and (3).
Total time is 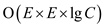 that
is
that
is .
.
Hence, the MAX-FLOW-BY-SCALING algorithm can be implemented as
it will take for its
execution.
for its
execution.
Bipartite Graph
A graph G (V, E) is the bipartite graph in
which V is made up of two collection of vertices such
that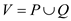 and each of
the edges of graph is as it joins a vertex from set P to the
vertex that lies in set Q. Consider the graph.
and each of
the edges of graph is as it joins a vertex from set P to the
vertex that lies in set Q. Consider the graph.
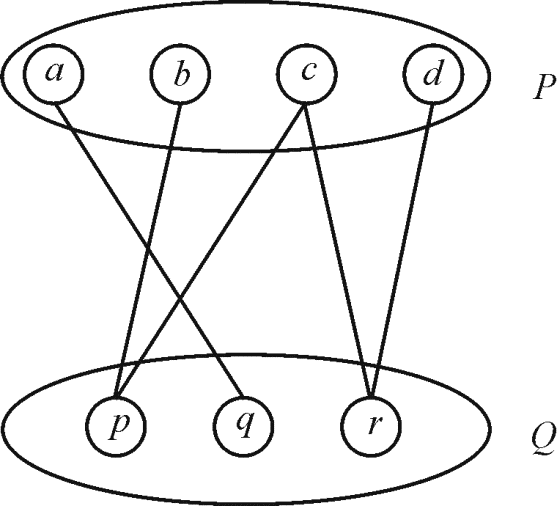
In the graph discussed above, the concerned set of
vertices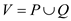 where
where
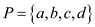 and
and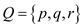 both the
vertex sets are disconnected mutually.
both the
vertex sets are disconnected mutually.
Matching: In a bipartite graph the matching is a group of edges such that any of its edges do not share the same end points. A vertex, included in the matched set of edges, is the vertex is used in creation of a matched edge is called as the saturated vertex.
For example: See the graph below which highlights the edges of matched set M.
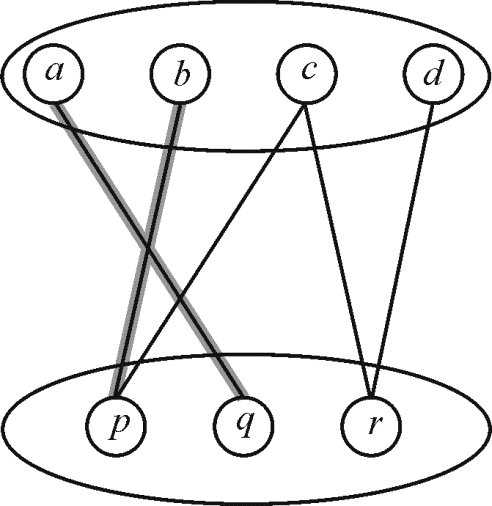
The matching set is as: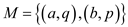 .
.
Matching is also called as maximal matching if there are no more edges that can be included into the matching set M and it is called the ideal or the perfect matching if no unmatched vertex is found.
For example: Consider the above graphand notice its highlighted edges:
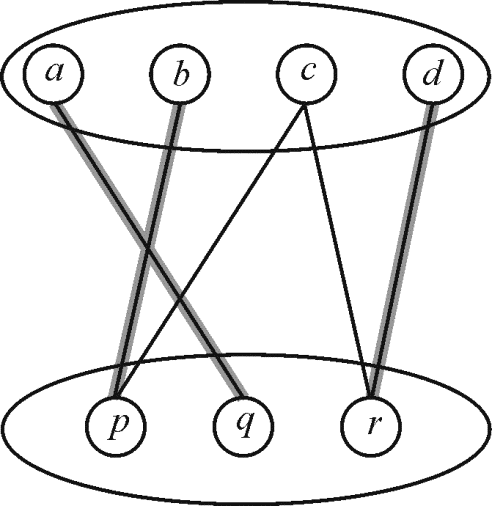
The matching set is as: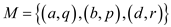 . The
matching shown in the above graph is maximal matching but not the
perfect matching because vertex c is not matched with any
other vertex.
. The
matching shown in the above graph is maximal matching but not the
perfect matching because vertex c is not matched with any
other vertex.
The Hopcroft-Karp bipartite matching algorithm: The
algorithm of Hopcroft-Karp bipartite matching is the faster
algorithm to search a maximum matching in a bipartite graph. More
specifically for a given bipartite graph say 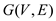 it takes
it takes
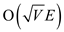 time to find a maximal matching.
time to find a maximal matching.
Consider that  is a
matching then a simple path P in G is called an
augmenting path with concern to the matching M if it starts
at a vertex which does not exist in the set of matched vertex and
end at an unmatched vertex and for every pair of subsequent edges
on P one of them is in M and another one is not. In a
graph a least possible augmenting path with reference to M
is the one which holds the lowest quantity of edges in it.
is a
matching then a simple path P in G is called an
augmenting path with concern to the matching M if it starts
at a vertex which does not exist in the set of matched vertex and
end at an unmatched vertex and for every pair of subsequent edges
on P one of them is in M and another one is not. In a
graph a least possible augmenting path with reference to M
is the one which holds the lowest quantity of edges in it.
Symmetric Difference of two collections of elements is a
set of elements which has only those items that are inexactly one
of the two concerned sets. That is given two sets A and
B the symmetric difference 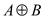 is defined
as
is defined
as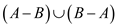 .
.
a. Consider that  as a
matching set and
as a
matching set and 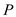 is an
augmenting path with concern to M that is the starting and
ending vertex of path P are not the vertices joining the
edges in the matching set of edges and there is alternate matched
and unmatched edges.
is an
augmenting path with concern to M that is the starting and
ending vertex of path P are not the vertices joining the
edges in the matching set of edges and there is alternate matched
and unmatched edges.
Now, since every augmenting path 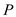 is
alternating and it starts at unmatched vertex and end at an
unmatched vertex. So, it must have possibly one edge more in its
unmatched edge that is
is
alternating and it starts at unmatched vertex and end at an
unmatched vertex. So, it must have possibly one edge more in its
unmatched edge that is 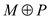 compared to
matched edges. So,
compared to
matched edges. So, 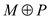 is a
matching and
is a
matching and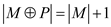 .
.
For example: Consider the following a bipartite graph:
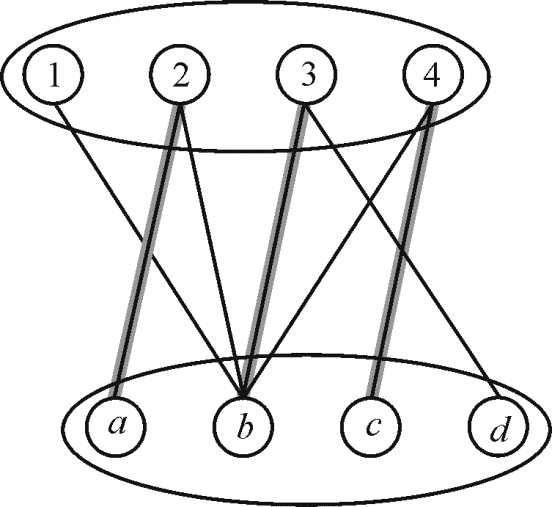
In this graph the matching 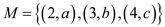 and the
path
and the
path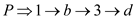 is an
augmenting path and the edge set of path
is an
augmenting path and the edge set of path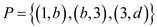 .
.
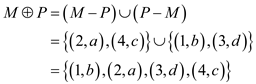
In the set M there are only three edges while in set
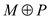 there are
four edges which is one more than the edges in M so
there are
four edges which is one more than the edges in M so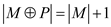 .
.
Now, consider are the
augmenting paths such that no two paths are having same vertices
with respect to
are the
augmenting paths such that no two paths are having same vertices
with respect to . Vertex
disjoint paths are the one having no internal vertex as common
among them.
. Vertex
disjoint paths are the one having no internal vertex as common
among them.

Now, in order to get the cardinality.

b. Consider that  and
and
 are
two matching in
are
two matching in . Since each
of
. Since each
of  and
and
 can contribute at most 1 each to vertex’s degree of set
can contribute at most 1 each to vertex’s degree of set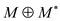 . So degree
can be at most 2 that are every vertex in graph
. So degree
can be at most 2 that are every vertex in graph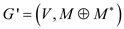 has a
degree at most 2.
has a
degree at most 2.
Since 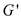 is graph of
vertices whose degree can be at most 2 so components of graph
should be either a path or a cycle or an isolated point. So it can
be concluded that
is graph of
vertices whose degree can be at most 2 so components of graph
should be either a path or a cycle or an isolated point. So it can
be concluded that 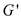 is a
disjoint union of simple paths or cycle. Edges of set
is a
disjoint union of simple paths or cycle. Edges of set 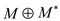 are
alternatively belong to
are
alternatively belong to  and
and . So each
cycle of above graph is even. Given that
. So each
cycle of above graph is even. Given that .
.
Since every path of 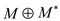 which is
not augmenting path with respect to
which is
not augmenting path with respect to  must have
equal number of edges form
must have
equal number of edges form  and
and
 since
since .
It can also be said that each such path has exactly one edge more
form
.
It can also be said that each such path has exactly one edge more
form  than
from
than
from . So there
is the need of at least
. So there
is the need of at least  such paths.
Since all these paths are vertex disjoint augmenting path having
starting and ending at unsaturated points.
such paths.
Since all these paths are vertex disjoint augmenting path having
starting and ending at unsaturated points.
 then
then
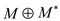 contains
least possible
contains
least possible vertex-disjoint
augmenting path with respect to
vertex-disjoint
augmenting path with respect to .
.c. Consider that 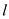 is the
length of the smallest augmenting path with the respect of
matching
is the
length of the smallest augmenting path with the respect of
matching of the graph
G. Let
of the graph
G. Let  be a
largest set of augmenting paths of uncommon vertices having length
be a
largest set of augmenting paths of uncommon vertices having length
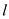 with respect to
with respect to .
Let
.
Let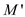 =
= and suppose
that P is a shortest augmenting path with respect
to
and suppose
that P is a shortest augmenting path with respect
to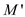 .
.
Since path 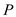 is which may
have some common vertices with
is which may
have some common vertices with therefore
therefore
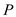 has
more than
has
more than 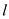 edges
otherwise it will oppose the fact that
edges
otherwise it will oppose the fact that be a
ultimate set of vertex-disjoint augmenting paths of length
be a
ultimate set of vertex-disjoint augmenting paths of length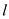 .
.
d. Consider that 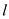 is the
length of the least possible augmenting path with reference to the
matching
is the
length of the least possible augmenting path with reference to the
matching . Assume
that
. Assume
that be a
superlative set of augmenting paths that have no vertex in common,
of length
be a
superlative set of augmenting paths that have no vertex in common,
of length 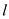 with
respect to
with
respect to . Let
. Let
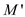 =
= and suppose
that P is a shortest augmenting path with respect
to
and suppose
that P is a shortest augmenting path with respect
to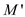 .
.
Consider that the concerned path P may have some common
vertices with that are
path P is not vertex disjoint with other paths. Assume that
Ais the collection of edges
that are
path P is not vertex disjoint with other paths. Assume that
Ais the collection of edges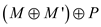 .Now,
.Now,
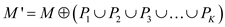 .
.
Therefore,

Now, consider 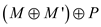 as an edge
set of a connected component
as an edge
set of a connected component 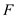 of the
graph
of the
graph so,
since
so,
since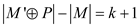 , therefore
, therefore
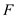 contains lowest of
contains lowest of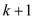 vertex-disjoint augmenting path with respect to least possible
length of each of such path is
vertex-disjoint augmenting path with respect to least possible
length of each of such path is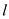 .
Therefore,
.
Therefore,

Now, since 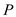 is not a
vertex-disjoint from other paths therefore it should have
necessarily a matching edge with some path corresponding
to
is not a
vertex-disjoint from other paths therefore it should have
necessarily a matching edge with some path corresponding
to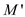 .
Hence, the path
.
Hence, the path 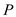 has more
than l edges.
has more
than l edges.
e . Consider the compact augmenting path in
the reference of matching has
has
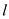 edges. Suppose that
edges. Suppose that  be another
matching. Since symmetric difference between
be another
matching. Since symmetric difference between  and
and
 will have at-least
will have at-least  augmenting
paths have no vertex in common. Each of the above paths will have
at least
augmenting
paths have no vertex in common. Each of the above paths will have
at least 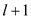 vertices.
Therefore,
vertices.
Therefore,
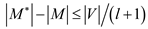
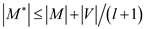
Hence, the cardinality of maximum number of matching in the graph will be:
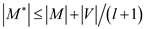 .
.
f. Finding augmenting paths, the HOPCROFT-KARP
algorithm repeatedly increases the size of a matching. This
algorithm avoids finding the augmenting path in each it executes
because its purpose is to find the ultimate set of smaller paths.
For this, only 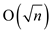 numbers of
iterations are needed.
numbers of
iterations are needed.
In this algorithm, every phasehas a single BFS (breadth first
search) and DFS (depth first search). Due to this, phases run in a
linear time fashion. Therefore, in a graph with 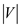 vertices and
vertices and
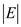 edges, and
for the first
edges, and
for the first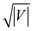 phases, it
will take a time of
phases, it
will take a time of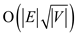 .
.
Each phase increases the length of lowest path that is
augmented, by one and searches biggest value length inthe provided
length. So in the completion of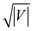 phase, there
are at least
phase, there
are at least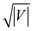 edges of the
shortest augmenting path.
edges of the
shortest augmenting path.
So, in the collection, if the path length is lowest of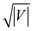 , then there
will be no more than a
, then there
will be no more than a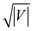 path length
and the most favorable matching differs from the span of M
by at most
path length
and the most favorable matching differs from the span of M
by at most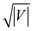 edges.After
iterations, the length of the lowest augmenting path will be at
least
edges.After
iterations, the length of the lowest augmenting path will be at
least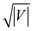 .
.
Therefore, the required number of repeat loop iterations
will be at most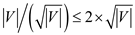 .
.
In this algorithm every phase increases the matching length by atleast one.
So, an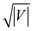 additional
phase is added to it before the algorithm terminates. Hence, there
are maximum
additional
phase is added to it before the algorithm terminates. Hence, there
are maximum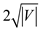 iterations
of repeat loop are possible in the algorithm.
iterations
of repeat loop are possible in the algorithm.
g. Consider that the graph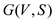 be a
bipartite graph. Let
be a
bipartite graph. Let 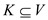 be a set of
incomparable vertices in
be a set of
incomparable vertices in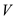 . For
searching the augmenting path having no two vertices in common, the
breadth first search and greedy approachcan be used. The algorithm
is as:
. For
searching the augmenting path having no two vertices in common, the
breadth first search and greedy approachcan be used. The algorithm
is as:
Breadth first search:
// execute the loop for each vertex in graph
for every vertex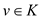
that alternates between matching and non matching edges,
stop the breadth first search at  level.
level.
In this case 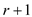 will be the
smallest form source to the free vertex in
will be the
smallest form source to the free vertex in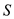 .
.
Let 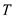 donates the
set of all vertices that are not matched and present in
donates the
set of all vertices that are not matched and present in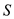
that are discovered at  level.
level.
Now performing a greedy approach,
// execute the loop for all the vertices that are not matching
for every vertex say 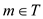
It is needed to do backtracking along its predecessor until the
vertex 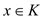 is found
successfully.
is found
successfully.
Now
// check for an unmarked vertex
if 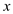 is
unmarked
is
unmarked
then saving the path between 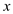 and
and
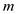
mark vertex 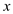 as
taken.
as
taken.
Since there is maximum E edges in the graph sothe
searching of the paths can be done in 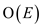 time. That
is it will take
time. That
is it will take 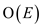 time to find
a maximal set of vertex-disjoint smallest augmenting path
time to find
a maximal set of vertex-disjoint smallest augmenting path  for a given
matching
for a given
matching . From above
the repeat loop will run at most
. From above
the repeat loop will run at most 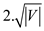 times.
Hence, the actual time taken by the HOPCROFT-KARP algorithm for its
execution will be
times.
Hence, the actual time taken by the HOPCROFT-KARP algorithm for its
execution will be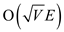 .
.