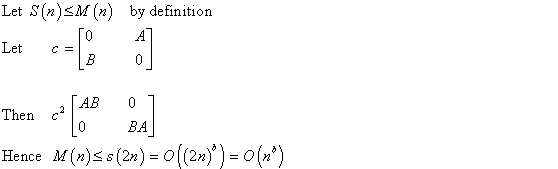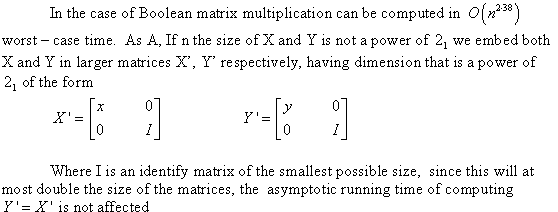Let M be an n*n matrix and assume 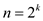 and
regularity condition is imposed such that
and
regularity condition is imposed such that 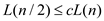 where c
< ½ and L(n) is the time taken to find an LUP decomposition of
n*n matrix. Decompose L such that:
where c
< ½ and L(n) is the time taken to find an LUP decomposition of
n*n matrix. Decompose L such that:
 where
where 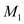 is
is 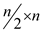 . Let the
decomposition of
. Let the
decomposition of 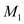 be
be  where
where
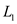 is
equal to
is
equal to 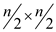 ,
, 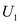 is equal to
is equal to
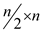 and
and  is equal to
is equal to
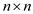 .
.
To attain the LUP decomposition of M, perform two LUP decompositions that are of half size, number of matrix multiplication and inversions that are constant.
The equivalence of matrix inverse and multiplication concludes that the run time is O(M(n))
BOOLEAN-MATRIX MULTIPLICATION (BMM) AND TRANSITIVE-CLOSURE RELATIONSHIP
A Boolean matrix is also called as a 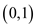 matrix
having entries with domain
matrix
having entries with domain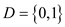 . It is a
matrix which is used to establish a relationship between various
sets.
. It is a
matrix which is used to establish a relationship between various
sets.
For better understanding of binary relation, consider a binary
relation R for the finite sets of elements, then use
adjacency matrix A whose row and the column are indexed as
P and Q 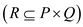 respectively to represent the R.
respectively to represent the R.
The entries of A are represented as,

 and 0
when
and 0
when .
.Example:
A binary relation is said to exist if the relationship as
uRv holds if u divides v completely. Here,
x and y belongs to different sets and R is the
relation between them. For the set 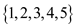 holds, the
set of pairs are as:
holds, the
set of pairs are as:
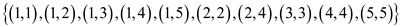 .
.
The Boolean matrix representation is as:

TRANSITIVE CLOSURE:
It is defined for a binary relation R on a set. It is denoted as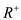 . It is such
that for a given set
. It is such
that for a given set 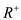 have R and
have R and
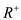 is
the minimal.
is
the minimal.Boolean Matrix Multiplication (BMM) Algorithm:
Consider X, Y is the two 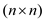 Boolean
matrices then the multiplication Z=X
Boolean
matrices then the multiplication Z=X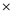 Y is
defined as,
Y is
defined as,
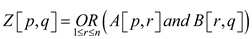 and implemented as,
and implemented as,
BMM (var x, y, z: nnboolean);
var p, q, r: integer
begin
for p:=1 to n do
for q: =1 to n do
begin
 : =false
: =false
for r: =1 to n do
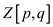 :=
:=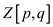 or
or
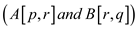
end
According to the question 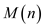 is the time
to multiply two
is the time
to multiply two 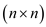 matrices
and
matrices
and 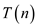 be the time
to find the transitive closure of the matrix.
be the time
to find the transitive closure of the matrix.
1. keep on multiplying the matrix, p to q to obtain in exactly 2 steps.
2. After the begin statement in above algorithm there is a checking step which divide the process in two parts and similarly it make the process of length log n (because of tree structure).
3. By keep on multiplying, transitive closure in the time
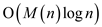 is
obtained. Generally, it is obtained by multiplying the matrix log
n times (checking after begin process).
is
obtained. Generally, it is obtained by multiplying the matrix log
n times (checking after begin process).
4. Each multiplication uses the concepts of Strassen’s multiplication.
Hence the 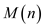 Boolean time
multiplication requires
Boolean time
multiplication requires 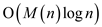 time for
transitive closure operation.
time for
transitive closure operation.
Consider the section 28.2 of the textbook,
The transitive closure  for a square
matrix C has to satisfy the condition
for a square
matrix C has to satisfy the condition
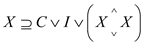 ,
,
Where I is the identity matrix and it can be defined as:
 ,
, 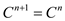 for
for
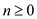 And
And
As product of Boolean matrix is associative, it can also be written as:
 .
.
Now as given in the question 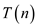 is the time
for computing transitive closure so according to the condition as
described above
is the time
for computing transitive closure so according to the condition as
described above 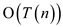 time
is required for Matrix-multiplication algorithm.
time
is required for Matrix-multiplication algorithm.
Refer textbook section 28.2 of chapter 28 for theorem 28.2.
The theorem 28.2 states that “matrix inversion is not harder than multiplication.”
The matrix inversion algorithm based on theorem 28.2 still works when elements are drawn from the fields of integer modulo 2.
Consider 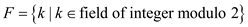 .
.
Consider the following matrix K that contains the elements from F.

Here, 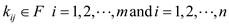 .
.
The regularity condition does not get affected by the division or multiplication of matrix elements by a specific number.
Hence, the condition for inversion gets satisfied.
The relevant positions of the elements are not changed. This fact can be used in the proof of the theorem for the matrix that contains elements of F.
The determinant is calculated as follows:

and
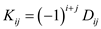
It is evident that, for a particular matrix element, this value is not going to be affected, except the sign. The reason is that the value of i and j for a particular element would remain same regardless of the change in location.
Therefore, it can be said that matrix inversion algorithm would work, even if the elements of the matrix are drawn from F (field of integer modulo 2).
MATRIX INVERSION METHOD
The main aim of matrix inversion algorithm is to change a matrix into its inverse form. It can also be used for proving that such inverses do not exist.
MATRIX INVERSION ALGORITHM FOR COMPLEX NUMBERS:
Generalize this algorithm using a numerical manipulation. Take a
 complex number array in following form:
complex number array in following form:
(Real part, Imaginary part: imaginary part, real part)
Now invert the above array. So, the inverse of original array is
 upper half
of the resultant array we got from inversion:
upper half
of the resultant array we got from inversion:
(Real part of inverse, imaginary part of inverse: imaginary part of universe, real part of universe)
Now following algorithm can be applied to get inversion of complex number:
1. Float inputreal[ ], inputimaginary[ ];
// enter the first array
2. Float outputreal[ ], outputimaginary[ ];
// entering the real part of complex number
3. int N;
4. int i, j;
5. Float m [ ,
,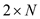 ];
];
// entering the second array
6. for (i=0; i<N; i++)
7. for (j=0; i<N; i++)
// complex number representation in matrix
8. m [i, j] = inputreal [i, j];
m [i, j +N] = inputimag[i, j];
9. m [i+N, j] = – inputimag [i, j];
M [i+N, j+n] = inputreal[i, j];
/ / inverting the matrix formed from above
10. matrix_invert(m);
// for inversion, either use the Cramer’s rule or theorem 28.2 of the book
11. for (i=0; i<N; i++)
12. for (j=0; i<N; i++)
13. outputreal[i, j] = m[i, j]; outputimag[i, j] = m[i, j+N];
The above algorithm will yield us Matrix inversion method for complex numbers.To know whether this method work correctly, consider a single
complex number of form 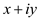 that we
want the inverse of. That is p and q, such
that
that we
want the inverse of. That is p and q, such
that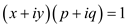 .
.
Using the format sample of the above algorithm (line 8 and 9)
Make the matrix M:

Now compute the inverse of the above array, which is to
solve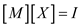 ,
,
Here I is the identity matrix.
Further using Cramer’s rule, the inverse of matrix M is:

Where Det. M= determinant of matrix M
Further, select the upper row of the matrix as the real parts
and imaginary parts: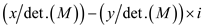
So, the output we have (consider the line 13 of the above
algorithm)
The result got by above steps is the inverse of (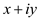 ).
).
Hence, generalization is true.
Above explanation is one method to solve the matrix inversion of a complex number.
Consider the theorem 28.2 of the book,
Consider a complex number matrix (can be formed from line 8 and 9 of the above algorithm),
Matrix of a complex number = A
A transpose of a complex matrix is equal to the matrix whose entries are replaced by its complex conjugate. This matrix is known as a Hermitian matrix.
A is a Hermitian matrix if,

Now consider the equation (28.11) of the book.
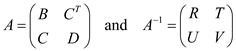
In the complex matrix, B=D and CT= –C (so C is a skew symmetric matrix)
And from the Hermitian matrix, 
Now consider the equation (28.12) of the book, apply the above comparison on it.

Now consider the equation (28.13) of the book.

This is the inversion of the matrix of a complex number.