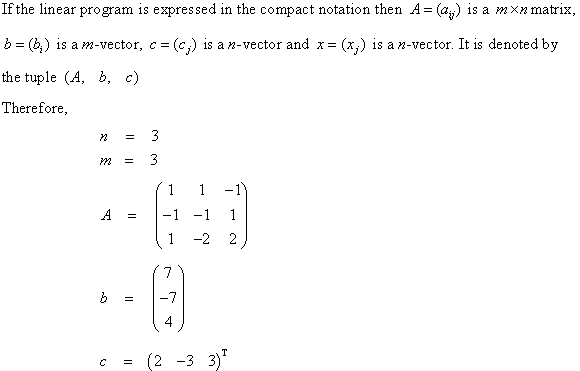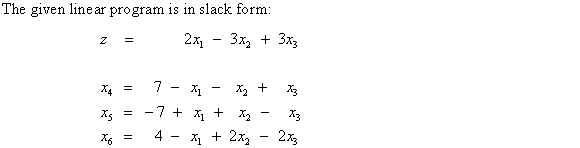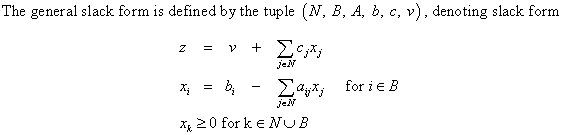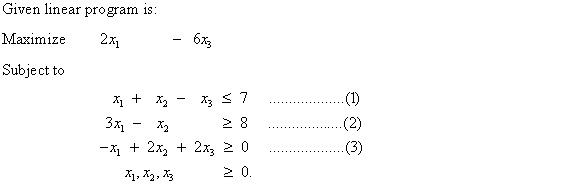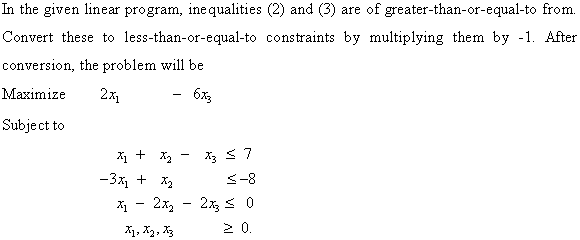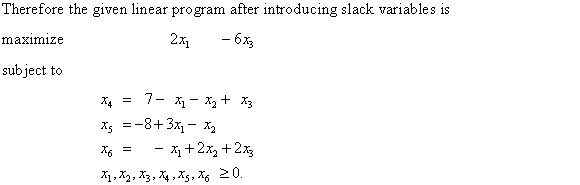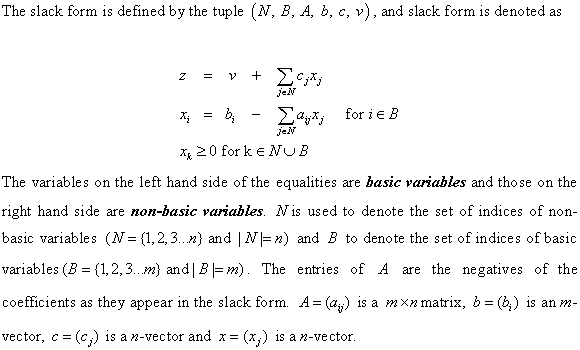Converting linear program into standard form
Linear programming is a way of achieving the maximum possible outcome from a set of resources that are represented as an integrated mathematical design.
In the technical terms the linear programming is a way to achieve optimum results from the linear programming problems. This optimization is subject to a few constraints.
Standard form of linear program:
In a standard form there is a set of p real numbers that
are , another
set of q real numbers that are
, another
set of q real numbers that are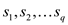 and a set
of
and a set
of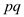 real numbers
that are
real numbers
that are where,
where,
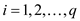
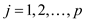
Now the objective is to find p real numbers such
that
such
that
Maximize
 … … (1)
… … (1)
And that is subject to
 … … (2)
… … (2)
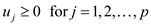 … … (3)
… … (3)
The first expression is called the objective function. The second and the third expression show the constraints.
This way a linear program can be put into the standard form.
Process of changing the linear program into the standard form:
There might be the following reasons that prevent the linear program from being in standard form: 1. The objective function is minimized while it should be maximized for being in standard form. 2. The variable in the program do not follow the non-negativity constraint. 3. The equality constraint is not in proper form that means there might be a ‘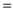 ’ sign
instead of ‘
’ sign
instead of ‘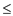 ’ sign. 4.
The inequality constraint might not be in proper form that mean
there might be a “
’ sign. 4.
The inequality constraint might not be in proper form that mean
there might be a “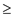 ” sign
instead of “
” sign
instead of “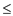 “sign.
“sign. does not
follow the non-negativity constraint. To remove this use
does not
follow the non-negativity constraint. To remove this use  as a
substitute for
as a
substitute for  and add the
non-negativity constraint
and add the
non-negativity constraint  and
and . 3. For the
third and fourthcase the expression can be gotten in the standard
form by multiplying the constraint with –1.
. 3. For the
third and fourthcase the expression can be gotten in the standard
form by multiplying the constraint with –1.Now, consider the below linear program:
Minimize
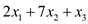
Subject to:

First step to convert the linear equation into standard form:
If linear program is in minimization form then convert it into maximization form by changing the sign of expression but there are no changes in subject to expression.Step 1:
Maximize
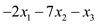
Subject to:

In above maximize expression, all variables have negativity constraint so to make those variables in non-negativity constraint; replace the variables accordingly such as:
 :
:Step 2:
Considering the above changes, new expression becomes as
Maximize
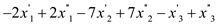
Subject to:

Now, converting the equality sign is into inequality sign;
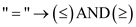
Step 3:
Maximize
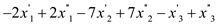
Subject to


Now, convert the greater than or equal to constraint to less than or equal to constraint by multiplying the –1 into the constraint.
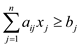
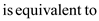

Step 4:
Maximize
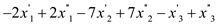
Subject to
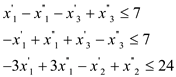

Now for consistency in variable names, rename them as below:


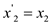
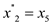

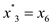
After combining all the steps, the following form of the expression is as:
Maximize

Subject to



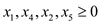

Convex region: A convex region is that it fulfills the requirement that for any two points in the region all points on a line segment between them are also in the region.
Feasible region: If the constraints form a convex region, then the region formed is called feasible region and the problem will have feasible solution.
Feasible solution: Any settings of the variables
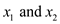 that
satisfy all the constraints (1), (2) and (3) is a feasible solution
to the linear program.
that
satisfy all the constraints (1), (2) and (3) is a feasible solution
to the linear program.
Objective values: The values obtained by substituting the
feasible solution values of the variables 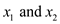 in the
objective function
in the
objective function  are called
objective values.
are called
objective values.
Optimal objective value and optimal solution: The maximum of all these objective values is called as optimal objective values and the feasible solution corresponding to these values is called as optimal solution.
Unbounded linear program: The linear program with some feasible solutions and does not have a finite optimal objective value is called as unbounded linear program.
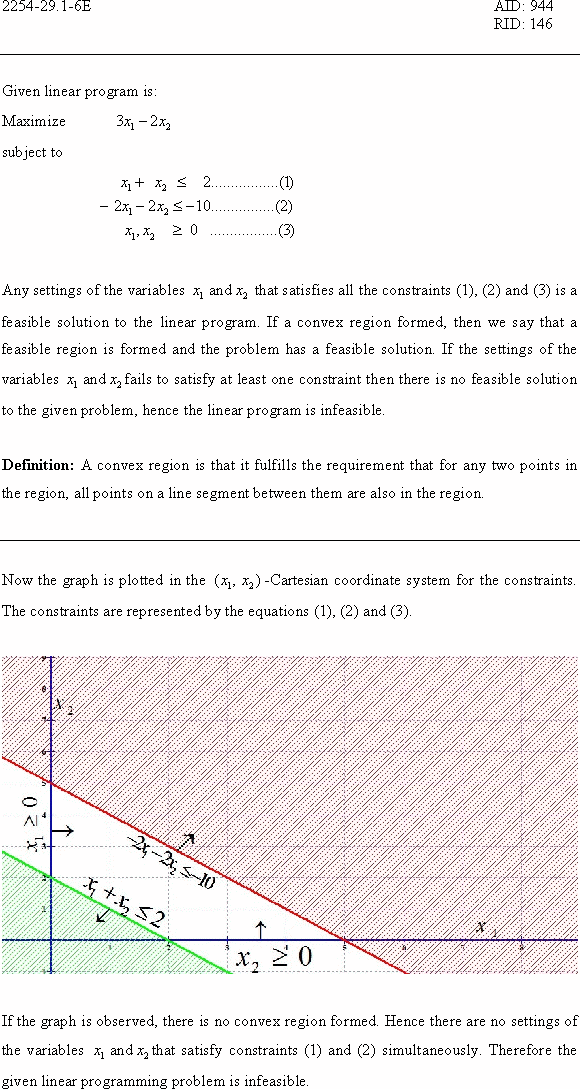
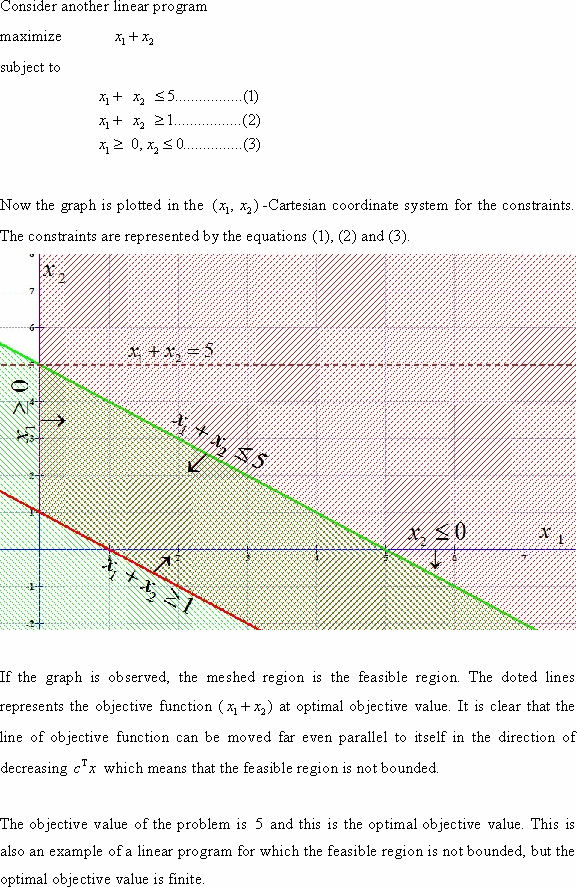
Consider the following linear program:
maximize 
subject to
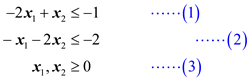
Now the graph is plotted in the  - Cartesian
coordinate system for the constraints. The constraints are
represented by the equations (1), (2) and (3).
- Cartesian
coordinate system for the constraints. The constraints are
represented by the equations (1), (2) and (3).
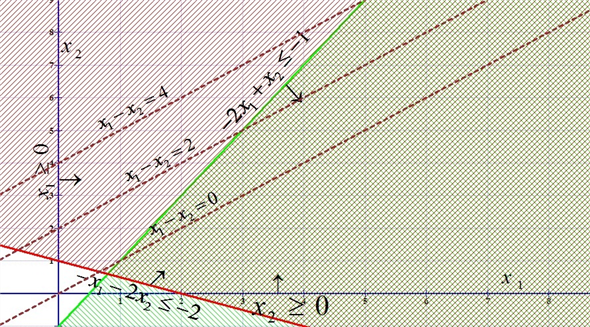
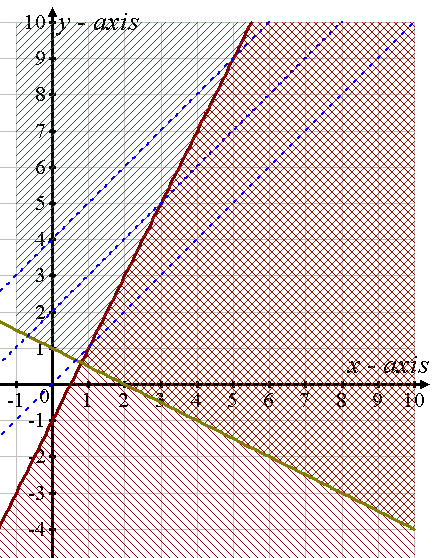
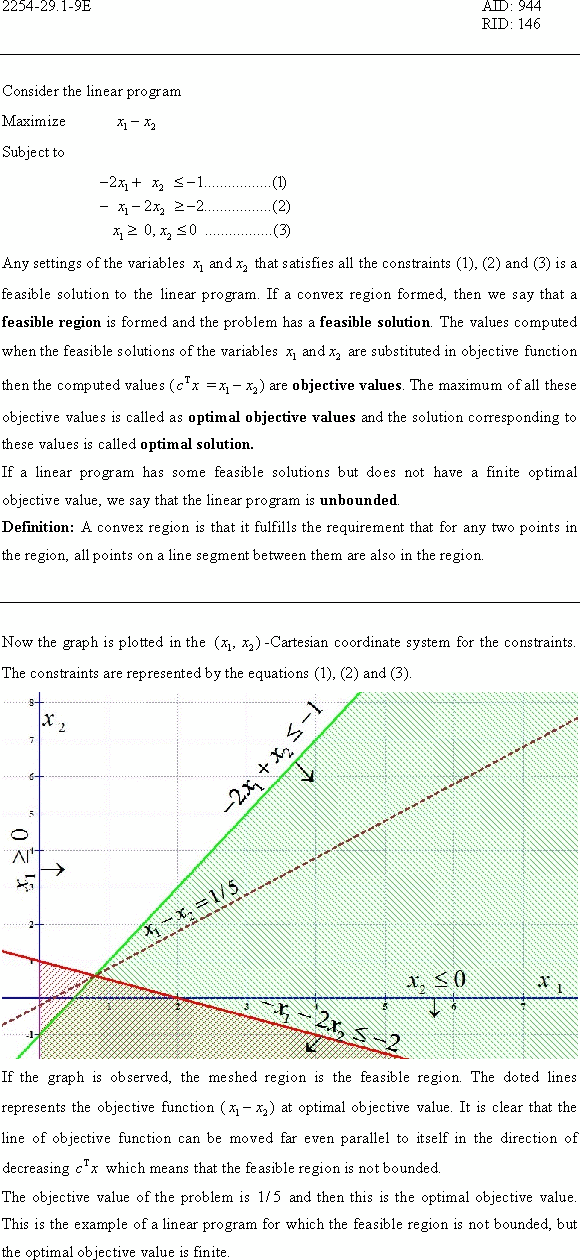
If the graph is observed, the meshed region is the feasible
region. The doted lines represent the objective function ( ) at
different feasible solutions. It is clear that the line of
objective function can be moved far even parallel to itself in the
direction of increasing
) at
different feasible solutions. It is clear that the line of
objective function can be moved far even parallel to itself in the
direction of increasing .
.
Therefore, the objective value can be made arbitrarily large and the problem has no finite maximum objective value or optimal objective value. Hence, the given linear programming problem is unbounded.