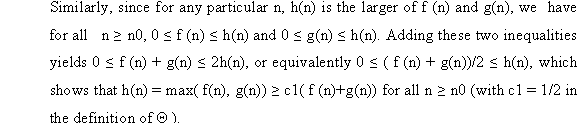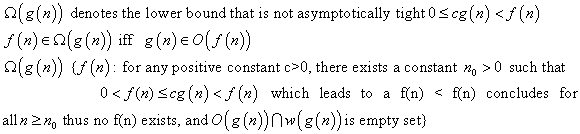The worst-case running time is denoted by 
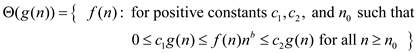
Now in order to show that  where
a and b are real constants and b > 0, it is
enough if the constants
where
a and b are real constants and b > 0, it is
enough if the constants  are found
that fits in the inequality
are found
that fits in the inequality
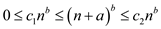
Now consider the following cases
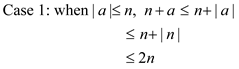
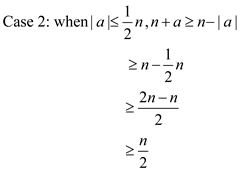
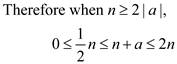
Now raise all parts of the inequality to the power of b

The constants obtained from the above inequality are  for
for
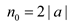
Hence showed that  where
a and b are real constants and b > 0,
satisfies
where
a and b are real constants and b > 0,
satisfies 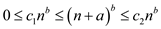 where
where
 and
and 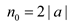
Consider 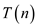 be the
running time of algorithm A.
be the
running time of algorithm A.
If the running time of the algorithm A is at least  , then
, then
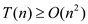 ……(1)
……(1)
From the equation 1, the asymptotically lower bound of algorithm A will be at least quadratic and can grow up to infinity.
From the definition of big , for a
function
, for a
function , the
asymptotically upper bound is,
, the
asymptotically upper bound is,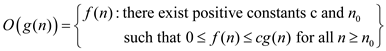
That is, 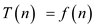 and
and
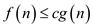 .
Therefore,
.
Therefore, 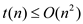 ……(2)
……(2)
From equation 2, asymptotically upper bound of algorithm A will be at most quadratic and can shrink up to zero since n is positive.
From equation 1 and 2, the time complexity of algorithm A can range from 0 to infinitely.
Therefore, the statement “The running time of an algorithm A at
least  ” is not
giving any conclusion about the time complexity of the algorithm
A.
” is not
giving any conclusion about the time complexity of the algorithm
A.
Hence, the statement “The running time of an algorithm A at
least  ” is
meaningless.
” is
meaningless.
The first Statement is true, and the Second is false.
Observe that

Also note

Hence 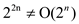 Since
Since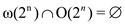 .
.
The following procedure is used to prove that
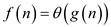 :
:
Theorem:
For any two functions 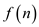 and
and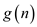 ,
it describes
,
it describes 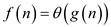 if and only
if
if and only
if 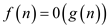 and
and 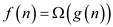
Proof:
Simply to say that, as the 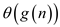
Definition implies that
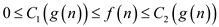
Here, it should satisfy both upper and lower bounds.
For example 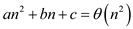 for any
constants
for any
constants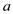 ,
,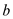 .
.
Here, 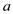 >0
immediately implies that
>0
immediately implies that 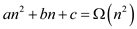 and
and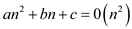 .
.
Since 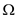 - notation
describes a lower bound, when we use it to bind the best-case
running time of an algorithm. So the running time of an algorithm
must fall between the
- notation
describes a lower bound, when we use it to bind the best-case
running time of an algorithm. So the running time of an algorithm
must fall between the 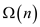 and
and
 .
It denotes lower bound and upper bounds respectively which are
nothing but the bounds specified by the
.
It denotes lower bound and upper bounds respectively which are
nothing but the bounds specified by the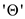 .
.
Notation:
Therefore 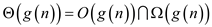
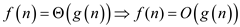
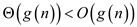 … (1)
… (1)
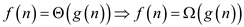
 … (2)
… (2)
From (1) & (2) we can say 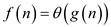
From the definition of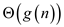 , consider
the inequality
, consider
the inequality
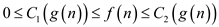
This inequality should satisfy both upper bound and lower bound.
This inequality can be split into two inequalities: 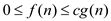 and
and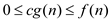 .
.
Now it is enough if proved that for an algorithm the worst-case
running time is 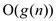 and the
best-case running time is
and the
best-case running time is .
.
For example 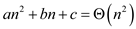 where a,
b, c are constants and
where a,
b, c are constants and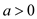 . This
directly implies that
. This
directly implies that 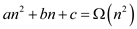 and
and
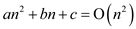
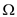 can be used to represent the best-case running time, as it denote
the asymptotic lower bound. So
can be used to represent the best-case running time, as it denote
the asymptotic lower bound. So 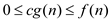 represents
represents .
.
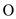 can be used to represent the worst-case running time, as it denote
the asymptotic upper bound. So
can be used to represent the worst-case running time, as it denote
the asymptotic upper bound. So 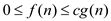 represents
represents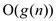 .
.
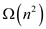 and
and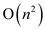 ,
and they denote lower bound and upper bounds respectively.
,
and they denote lower bound and upper bounds respectively.Now considering the worst-case running time as 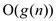 and the
best-case running time as
and the
best-case running time as , it is
enough to prove that the running time of an algorithm is
, it is
enough to prove that the running time of an algorithm is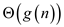 .
.
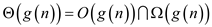
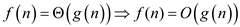
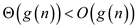 …… (1)
…… (1)
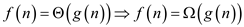
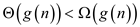 …… (2)
…… (2)
From (1) & (2) it can be said 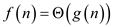
Hence proved that the running time of an algorithm is 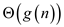 if and only
if the worst-case running time is
if and only
if the worst-case running time is 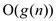 and the
best-case running time is
and the
best-case running time is .
.
The definition for 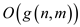 is as
follows:
is as
follows:
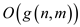 ={
={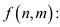 there exist
positive constants
there exist
positive constants  and
and
 such that
such that
 for all
for all 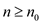 and
and
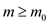 }
}
The corresponding definition for 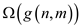 is as
follows:
is as
follows:
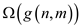 = {
= {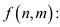 there
exists positive constants
there
exists positive constants  and
and
 such
that
such
that
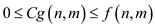 whenever
whenever 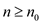 and
and
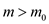 }
}
The corresponding definition for 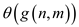 is as
follows:
is as
follows:
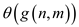 ={
={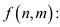 there exists
positive constants
there exists
positive constants  and
and
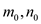 such that
such that
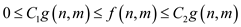 for all
for all 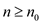 and
and
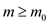 }
}