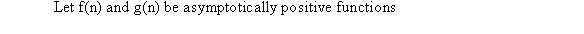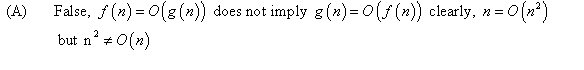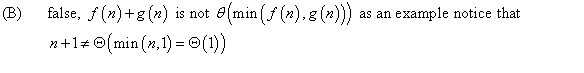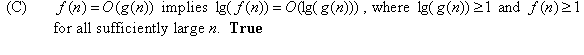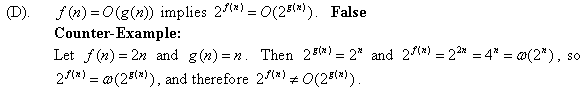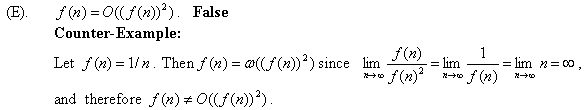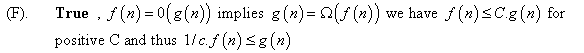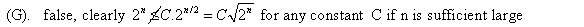Consider the following polynomial:
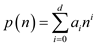
Here,  be a degree
be a degree
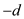 in
in
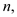 and let
and let  be a
constant.
be a
constant.
The polynomial can be rewritten as shown below:

Consider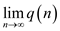 .
.
As 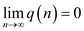 , so there
must be an integer
, so there
must be an integer  such that
such that
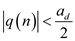 for all
for all 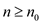 .
.
So 
Let 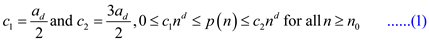
a.
If 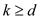 , then
, then
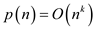
For a given function m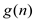 , denote
, denote
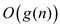 as
the set of functions given by
as
the set of functions given by
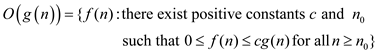
From the given statement 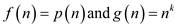 , where
, where
 is
a constant.
is
a constant.

From equations (1) and (2),

Hence from the definition, 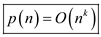 .
.
b.
If 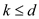 , then
, then
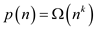
For a given function 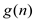 , denote
, denote
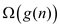 as
the set of functions given by
as
the set of functions given by

From the given statement 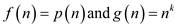 , where
, where
 is
a constant.
is
a constant.

From equations (1) and (3),
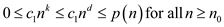
Hence from the definition, 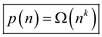 .
.
c.
If 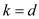 , then
, then
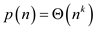
For a given function 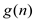 , denote
, denote
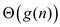 As
the set of functions given by
As
the set of functions given by

From the given statement 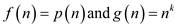 , where
, where
 is
a constant.
is
a constant.
From equation (1),
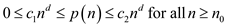
Hence from the definition, 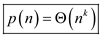 .
.
If 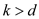 , then
, then
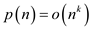
For a given function 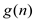 , denote
, denote
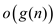 as
the set of functions given by
as
the set of functions given by
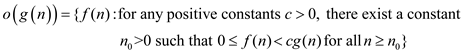
From the given statement 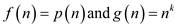 , where
, where
 is
a constant.
is
a constant.

From equations (1) and (4),

Hence from the definition, 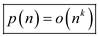 .
.
e.
If 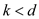 , then
, then
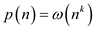
For a given function 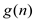 , denote
, denote
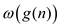 as
the set of functions given by
as
the set of functions given by
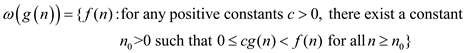
From the given statement 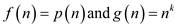 , where
, where
 is
a constant.
is
a constant.

From equations (1) and (5),
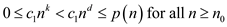
Hence from the definition, 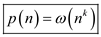 .
.
Relative asymptotic growths:
L' Hospital's Rule: In the case where f(n) and g(n) are differentiable functions and
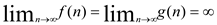 , the limit
of
, the limit
of 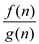 can be
computed as the limit of their derivatives
can be
computed as the limit of their derivatives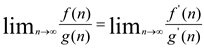 .
.
Justifications:
(a)
Apply L' Hospital's Rule k times,

Hence,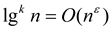 .
.
(b)
By 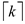 applications of L' Hospital’s rule,
applications of L' Hospital’s rule,
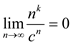
Hence,  .
.
(c)
sin n is a periodic function and takes the values in the range [-1, 1].
When sin n=1, 
When sin n = -1, .
.
(d)
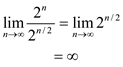
Hence, 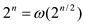 .
.
(e)
Consider 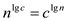
Take log on both sides.
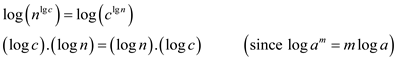
(d)
Consider 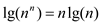 .
.
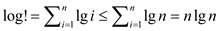 and thus
and thus 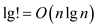

And thus, 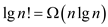
Finally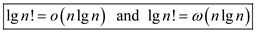
The limit  lies in the
interval [1/2, 1].
lies in the
interval [1/2, 1].
a.
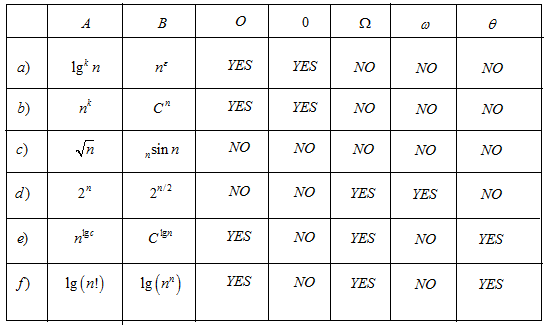
Consider the following provided 30 functions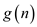 :
:
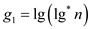 ,
,  ,
,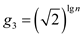 ,
,  ,
, ,
,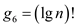 ,
, ,
, ,
, 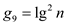 ,
, 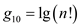 ,
,  ,
, 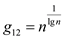 ,
, 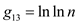 ,
, 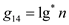 ,
, 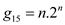 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
, 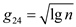 ,
,  ,
, 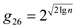 ,
,  ,
, 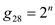 ,
, 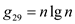 ,
, 
Consider the following expression to arrange the function:
• The growth of exponential function is larger than any
polynomial function. This means that the functions  and
and
 are
the 2 greatest function.
are
the 2 greatest function.
• It is already known .
.
This implies

or,

Now, apply power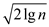 on both
sides, therefore
on both
sides, therefore

• Consider function 
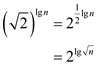
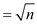 (By using the binary logarithm).
(By using the binary logarithm).
• The iterated logarithmic functions are very slowly growing function.
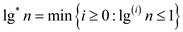
The value of  is the
minimum number of logarithmic iteration at
is the
minimum number of logarithmic iteration at  is less than
1.
is less than
1.
Consider the following  function:
function:
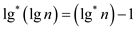
Consider the following  function:
function:

Where, 
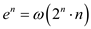
• Consider the following  function:
function:
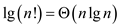 Using equation (3.19)
Using equation (3.19)
• Consider the following  function:
function:
 Using equation (3.18)
Using equation (3.18)
Therefore, the following is the different equivalence class of
each term. Here, the symbol > denotes 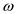 notation.
notation.
b.
Consider the following non-negative function 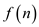 for all
function
for all
function  of part
(a).
of part
(a).

For any value of n, the best and worst time complexity of
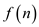 cannot be
cannot be
 and
and
 .
.
a.
Asymptotic notation is used to describe the running time of algorithm in term of function.
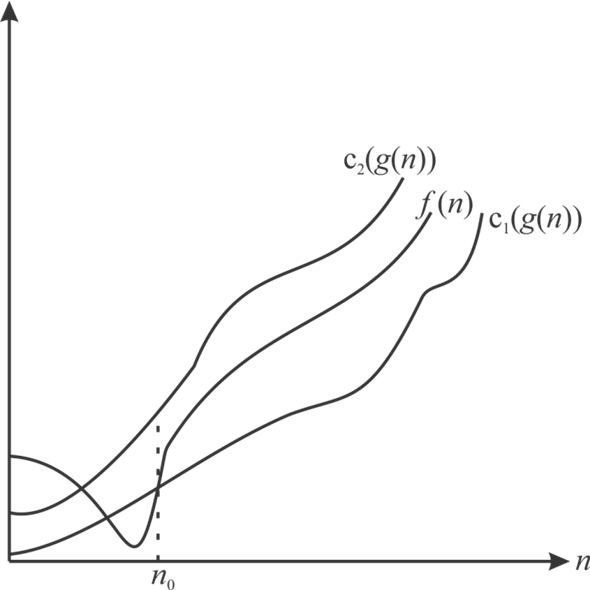
big(O) notation: upper bound in above graph represents the big(O) notation.
 …… (1)
…… (1)
 notation: lower bound in above graph represents the
notation: lower bound in above graph represents the
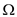 notation.
notation.
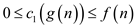 …… (2)
…… (2)
In both equation (1) and (2),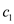 and
and
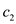 are the positive constant
are the positive constant
 is asymptotically non-negative for all the positive constants
c,
is asymptotically non-negative for all the positive constants
c,
Such that
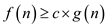
Since, from equation (2), the constant c is positive
So,
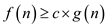 …… (3)
…… (3)
Similarly, from equation (1),
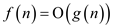 …… (4)
…… (4)
Hence, from equation (3) and (4),
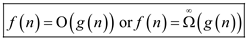
b.
First discussion is on the omega and the omega infinity notation and then on the basis of this second discussion will be on its advantage or disadvantage,
Omega notation: It is denoted by symbol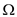 . It is an
asymptotic lower bound notation. It is defined as,
. It is an
asymptotic lower bound notation. It is defined as,
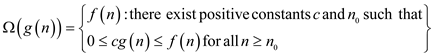
Whereas,
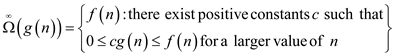
Advantage:
• It has a wider range of values for the notations so a large range of the complexity
• can be analyzed.
• In 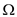 notation
the resource utilization is maximum.
notation
the resource utilization is maximum.
• In 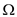 notation
running time of algorithm will be minimum.
notation
running time of algorithm will be minimum.
Disadvantage:
As the range is not fixed so it is not possible to determine its limitation and its consequences to an indefinite analysis.
c.
Consider the theorem 3.1,
When 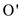 is
substituted in place of
is
substituted in place of 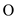 but in the
theorem 3.1
but in the
theorem 3.1 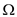 is used,
then the” if and only if” direction will have modification as:
is used,
then the” if and only if” direction will have modification as:
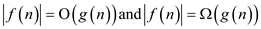
Because from the author definition,
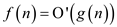
If and only if
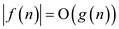
d.
Consider the following formula of the soft theta and soft omega:
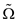 (Soft omega):
(Soft omega):
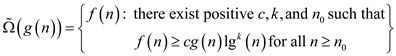
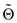 (Soft theta):
(Soft theta):
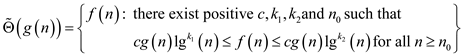
For any two function f(n) and g(n),
the function 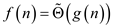 if and only
if
if and only
if 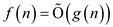 and
and 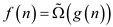 .
.
• These notation are similar to older one only difference is that here the logarithms factor extra added to them.
• This logarithm function used in the case of larger inputs.
• From the definition soft-oh is lower bound in nature and soft-omega is upper bound in nature and soft theta lies in between them.
So, it is obvious that if any function is equal to soft-theta then that function is also equal to soft omega.
Consider the following iterated function:
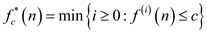
In above equation  is an
iterated function of f which is iterated
ith times to reduce it to c or less than
c.
is an
iterated function of f which is iterated
ith times to reduce it to c or less than
c.
a.
Consider the following function:
It is required to reduce that function to 0 that is the values of c is 0.
Suppose the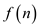 is iterated
1 more time therefore the
is iterated
1 more time therefore the  becomes:
becomes:
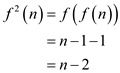
Similarly, when 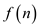 is iterated
n time therefore, the
is iterated
n time therefore, the become:
become:
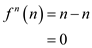
Therefore, it is required to iterate n times function f to reduce it to 0.
Hence, the iterated  must
be
must
be 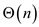 .
.
Consider the following function:
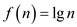
It is required to reduce that function to 1 that is the values of c is 1.
In logarithmic term when base is equal to its argument then only its answer gets 1.
Therefore, it is required to iterate 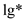 times
function f to reduce it to 1.
times
function f to reduce it to 1.
Hence, the iterated  must
be
must
be 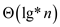 .
.
Consider the following function:
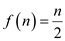
It is required to reduce that function to 1 that is the values of c is 1.
Suppose the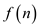 is iterated
1 more time therefore the
is iterated
1 more time therefore the  becomes:
becomes:
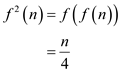
Now, 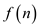 is again
iterated, therefore the
is again
iterated, therefore the  becomes:
becomes:

After every iteration the function f gets halves itself.
Similarly, when 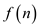 is iterated
is iterated
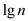 time
therefore, the
time
therefore, the become:
become:

Therefore, it is required to iterate 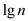 times
function f to reduce it to 1.
times
function f to reduce it to 1.
Hence, the iterated  must
be
must
be 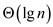 .
.
Consider the following function:
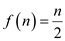
It is required to reduce that function to 2 that is the values of c is 2.
Suppose the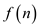 is iterated
1 more time therefore the
is iterated
1 more time therefore the  becomes:
becomes:
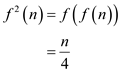
Now, 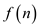 is again
iterated, therefore the
is again
iterated, therefore the  becomes:
becomes:

After every iteration the function f gets halves itself.
Similarly, when 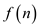 is iterated
is iterated
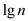 time
therefore, the
time
therefore, the become:
become:

In 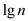 times the function f is reduces it 1. When
function f is iterated one less than
times the function f is reduces it 1. When
function f is iterated one less than
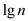 times then the value of function f at
times then the value of function f at
 will
double the value at
will
double the value at 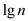 times that is 2.
times that is 2.
Hence, the iterated  must
be
must
be 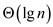 ,
ignoring the constant.
,
ignoring the constant.
Consider the following function:
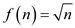
It is required to reduce that function to 2 that is the values of c is 2.
Suppose the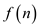 is iterated
1 more time therefore the
is iterated
1 more time therefore the  becomes:
becomes:

Now, 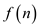 is again
iterated, therefore the
is again
iterated, therefore the  becomes:
becomes:

After every iteration the function f power gets halves
itself. Therefore after p iteration the 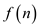 become:
become:
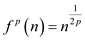
After p iteration,  .
Therefore, the value of p becomes
.
Therefore, the value of p becomes
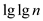 .
.
Hence, the iterated  must
be
must
be 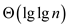 to
reduce function f to 2.
to
reduce function f to 2.
Consider the following function:
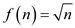
It is required to reduce that function to 1 that is the values of c is 1.
Suppose the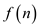 is iterated
1 more time therefore the
is iterated
1 more time therefore the  becomes:
becomes:

Now, 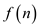 is again
iterated, therefore the
is again
iterated, therefore the  becomes:
becomes:

After every iteration the function f power gets halves
itself. Therefore after p iteration the 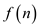 become:
become:
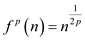
After p iteration, 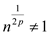 .
.
Hence, it is not possible to reduce function f into 1.
Consider the following function:
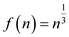
It is required to reduce that function to 2 that is the values of c is 2.
Suppose the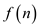 is iterated
1 more time therefore the
is iterated
1 more time therefore the  becomes:
becomes:

Now, 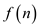 is again
iterated, therefore the
is again
iterated, therefore the  becomes:
becomes:

Therefore after p iteration the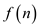 become:
become:
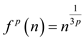
After p iteration,  .
Therefore, the value of p becomes
.
Therefore, the value of p becomes
 .
.
Hence, the iterated  must
be
must
be  to
reduce function f to 2.
to
reduce function f to 2.
Consider the following function:
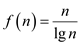
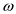 notation is
used to determine lower bound it is because it is not
symptomatically tight. Definition is as follows:
notation is
used to determine lower bound it is because it is not
symptomatically tight. Definition is as follows:
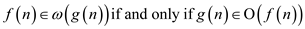
Now, define 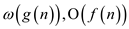 as a
set.
as a
set.

Hence, the iterated  will
be
will
be 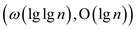 to
reduce function f to 2.
to
reduce function f to 2.