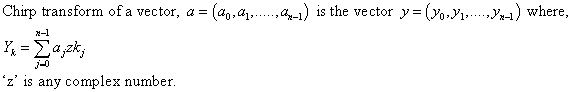To Prove: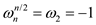

Here, is the complex root of unity such that: .

There are exactly n complex 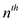roots of unity: 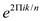for .

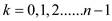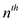Therefore, is the principal root of unity.

Step 1: Let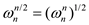

Now substituting the value of 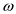as

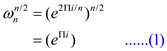
For 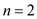, the expression in can be written as: .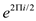

Therefore,

Step 2: According to the definition of the exponential of a complex number:

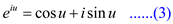
Since,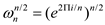

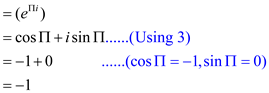
Hence,

Consider the given coefficient vector a = (0, 1, 2, 3). The Discrete Fourier transformation (DFT) is the vector y=. The DFT can be expressed in the general form(y= ) as follows:

Now, multiply the 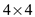vandermonde matrix and 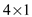coefficient matrix. Thus, the resultant 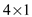matrix is as follows:

…… (1)

Each row value is equals to corresponding element in the left side matrix. Therefore solve the right hand side matrix to calculate the values of and.

Consider the values 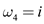and 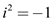to calculate the vector elements.

Thus, 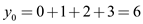…… (2)

Similarly calculate the value of

…… (3)

Put the value 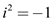in equation (3)

Thus,

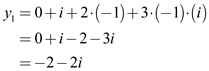
Calculate the value of as follows:

Hence, 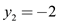…… (4)

Calculate the value of as follows:

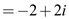
Hence, 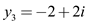…… (5)

From equation (2) , (3) , (4) and (5), the value of and are as follows:

The polynomials are as follows:

and

The evaluation is done using the fourth roots of unity that is, .

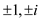• Call RECURSIVE-FFT ((-10, -1,0,0)) and evaluate to (-11, -10-i, -9, -10+i)

• Now evaluate the original function call, the values are ,.

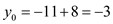• On changing the values, we have 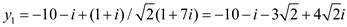and

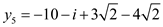
• Similarly, if it is required to compute the FFT of other polynomial, get the FFT of B(x) as

On interpolation, the result is as follows:

The polynomial is: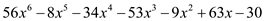

Discrete Fourier transform (DFT) is invertible with

=

where is the inverse of vandermonde matrix.

So,

where is the root of unity.

The inverse DFT which is is calculated as follows.

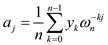
where is the inverse DFT, is the coefficient vector. is the nth root of unity.

At first compute the Discrete Fourier transform (DFT) to obtain the value of then flip the sequence by fixing the .

Pseudo code of is as follows:

INV-DFT (y)

// store length of vector y

1. n= y. length

// check the value of variable n

2. if n==1

//return the value of vector

3. return y

// is the principle nth root of unity and is its inverse

4.

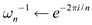
5.

//split the vector into even and odd part and store it into coefficient vector of y

6.

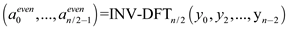
7.

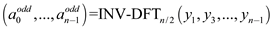
//for loop is used to flip the sequence

8. for j=0 to n/2-1

9.

10.

//it is used for mapping

11.

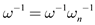
//if statement is used to find the value of coefficient vector

12. if j=0

13.

14. else

15.

//return the column vector

16. return a

• In line first store the length of vector y into variable n so the worst case complexity will be.

• Line 2-3 is used to check the element of DFT, so the complexity will be.

• Line 5-6 of pseudo-code is used to define the coefficient vector for polynomial so the complexity will be.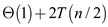

• Line 8-9 is used to find the value of so each invocation takes.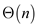

• Line 12 and 14 calculate the value of by dividing every term to n. This creates another factor which can be neglected by doing the division step along with the previous step.

So the total time complexity will be as follows:

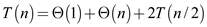
By using master’s theorem, the following time complexity is obtained:

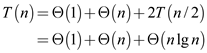
The highest order term decides the complexity.

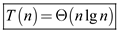
In the above recurrence of running time, represent the length of input vector. Evaluate a polynomial of degree n at nth root using inverse DFT.

By using FFT (Fast Fourier Transform) which takes the advantage of the special properties of the complex roots of unity.

FFT method employs a divide and conquer strategy using even index and odd index coefficients of A(x) separately to define the three-new degree bound n/3 polynomials 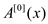, and

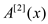
These polynomials are expanded as follows:

Evaluate the degree bound n/2 polynomials 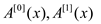and 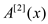at the points

Combine the results obtained.

By applying the halving lemma, the list of values consists not of n distinct values but only of the n/3 complex 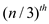roots of unity with each root occurring exactly twice.

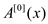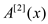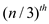Therefore, the polynomials , and of degree bound n/3 are recursively evaluated at the n/3 complex roots of unity.

These sub problems have the same form as the original problem but are half the size.

Thus, an n element 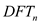computation is divided into two n/3 elements computations.

This decomposition is the basis for the following recursive FFT algorithm which computes DFT of an n element vector where n is the power of 3.

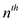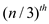For n to be a power of 3, that the cube of the complex roots of unity are the n/3 complex roots of unity apply the cancellation lemma,

Therefore,

Now, write and define 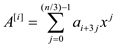for i=1,2,3…

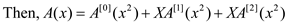
The recurrence which is obtained is:

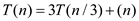
Solving the recurrence relation using Master’s theorem:

Compare the above recurrence by standard formula:

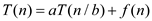
Here, a=3, b=3 and f(n)=n. Computing the value of 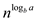the value obtained is 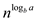=1

On comparing the values of 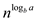and f(n) which are same the case 2 of master’s theorem is applied.

So, the final running time complexity is:

The procedure is described by the following algorithm:

RECURSIVE-FFT-INVERSE(y)

1 n=y. length

2 if n==1

3 return y/n

4 end if

5

6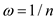

7

8

9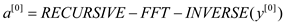

10 for k = 0 t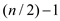o do

11

12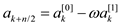

13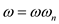

14 end for

15 return a

To prove that 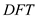and inver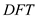se are well defined in the given system , suppose be the ring of integers .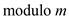

Where, 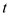is a positive integer and is even integer

Then,

Now, construct a polynomial 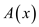such that

Where 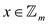and polynomial 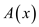is of degree-bound 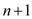with coefficients from

Now, define such that

Then, the vector is discrete Fourier transformation of the coefficient vector

Now, show that product and sum of two distinct tuples of the vector 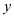is again the tuple of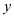

Since,

Then,

Then, take product and sum of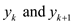

And

Then, the product and the sum of two distinct tuples of the vector 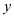is again a tuple of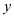

Therefore, discrete Fourier transformation (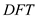) is well defined

Now, write the discrete Fourier transformation as the matrix product

Then,

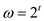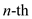Where, as the principal root of unity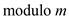

Since, the square matrix is a non-singular matrix in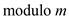

That is

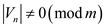
Then, exists

Now, multiply from left side by in the equation

Then,

Or

Then, it can be written as

Since, exists

Therefore, is well defined in .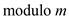

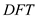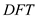Hence, and inverse are well defined in the system.

Finding the coefficient of a polynomial of bounded degree

MULTIPLYING-OUT algorithm is used to find the coefficients of polynomial P(x) of degree bound n+1 that has zeroes. This algorithm uses the property of recursive calls; every recursive call made here is of size.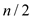

The Multiplying-Out algorithm takes input as the list of values that are provided by the user. After this, it is checked whether the list has one single item or not, if the condition satisfies, return the value of. It is returned because the polynomial has the value zero at z_j, only when the polynomial will be a multiple of. After this, the list has been divided into two lists (P₂(x) and P₂(x)) and recursion is done in list items.

After this, fast Fourier Transform is done on both lists and their values is stored in variables y₁ and y₂. Make use of for loop to calculate the value of y and then perform Fourier transform inverse storing values in P(x).

Multiplying-Out algorithm is given below:

MULTIPLYING-OUT ALGORITHM: (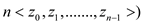

// use of if condition to check whether list has a single element or not

1. if n = 1

return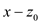

2. else

// Divide the list into two parts, where P₁(x) contains list items 1 to n/2

// and P₂(x) contains rest of them and recursion is performed on both list items

3. P₁(x) = Multiplying Out

4. P₂(x) = Multiplying Out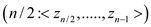

// perform fast Fourier transform on P₁(x) and P₂(x)

5. (y₁ is a vector of 2n values).

6. 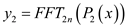(same for y₂)

// Compute the point wise product y of y₁; y₂ in linear time

7. for()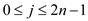

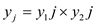
// Perform inverse of evaluation to find the coefficient of polynomial using

// point-value representation

8.

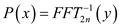
For determining the runtime, following should be taken into consideration:

1. Lines 1, 2, 7 take time in total.

2. There are 2 recursive calls to Multiplying Out of size n=2 each (lines 3, 4).

3. There will be a total of three calls FFT (fast Fourier transform) of size 2n

(lines 5, 6, 8).

Therefore, total running time will be:

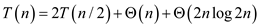
Considering the recursion tree of Multiplying-Out, the height of this tree will be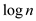. It is so because at every recursive call made, the input size is partitioned into half. This can be performed only in 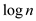times before n is minimized to the base 1.

At each level 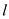(with 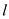= 0 making it the top level). The algorithm will make recursive calls of size . The algorithm will have cases of extra work for level 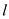, the FFT (fast Fourier transform) of current active calls have been carried out making use of 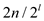roots of unity point.

In reality, it is found that it is useless to add any value for the recursive calls stated in since their work is counted in the extra work in lower branches of the tree.

So, at level 0, the total work is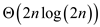

At level 1, the running time can be given as:

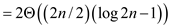
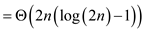
At level l, the running time can be given as:

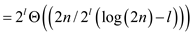
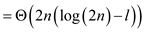
Therefore, the running time at any particular level 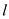is.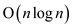

There will be 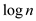levels in the algorithm which takes time of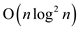.