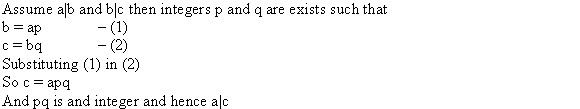Proof of the given equation

Supposed equations are:

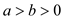…… (1)

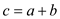…… (2)

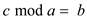
Here c is the number which is being divided that is c dividend so according to formula:

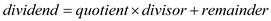…… (3)

So 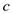can be represented as:

…… (4)

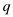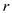Where represents the quotient, a represents the divisor andrepresents the remainder.

Now dividing number c by a

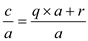
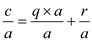…… (5)

Removing a from both nominator and denominator from equation (5)

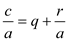…… (6)

Now dividing equation (2) by a

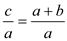
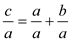
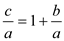…… (7)

Comparing the equations (6) and (7)

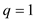
Hence it proves:

.

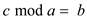A number can be called as prime number when it is only divisible by itself and 1.

Some prime numbers are 2, 3, 5, 7, 9 and so on.

Assume p is a prime number and k is any number less than p.

Suppose 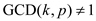and assume 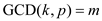for any 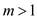and .

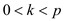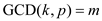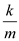Using the property of GCD, if then and .

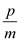That is

where and are constants.

Calculate the value of m from (1).

Put value of m into (2)

Consider is d, so.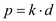

Hence k divides p which is a contradiction as p is a prime number.

The assumption that 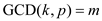is not correct.

So, .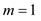

Therefore, 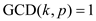if .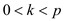

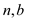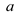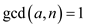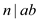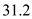For all positive integers and, it is given that and. Now, consider the theorem, according to this theorem,

If 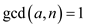then,

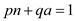, for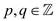 …… (1)

Here, it is given that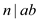. So, from the above equation (1) it is clearly seen that divides 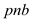and.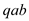

Now, 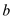can be written in the following ways:

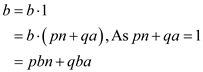
Hence, it can be concluded from the above that, 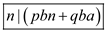or .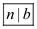

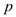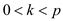To prove: If is prime and, then.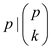

First simplify the above given expression, then;

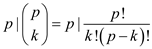
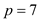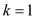Now, check it for and, then the above expression will be;

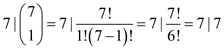
Therefore, it is true for 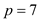and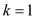. In the same way, 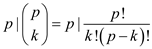is true for all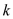, where.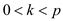

Now, consider the given expression and simplify it as follows:

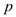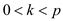Also, it is already known that, if is prime and, then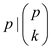. Therefore, 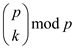will be zero, if 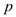is prime and.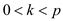

So, the above expression becomes,

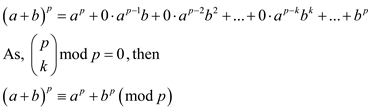
Hence, for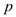is prime and,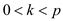

It is given that 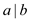then 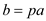for some integer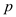. Assume that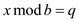, then user has,

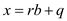, for some integer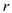 …… (1)

Now put the value of 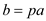in the equation (1). So, user obtained,

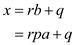
Therefore,

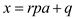, for some integer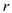 …… (2)

From the equation (2),

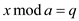, because in the equation (2), the value of 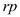is also an integer.

Hence,

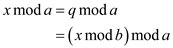
Hence,

Now consider that, .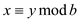

Therefore,

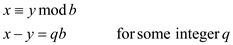
Now, put 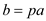from the given assumption.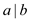

Therefore,

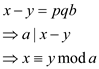
Hence,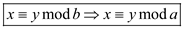

Greatest common divisor (gcd) of two integers:

Consider two integers a and b. If d is a largest common divisor of a and b, that is, d divides a and d divides b, then d is called gcd of a and b.

Consider the equation 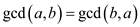to prove.

Assume that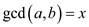. That is, x divides a and x divides b.

Since,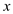divides b and also divides a, x is the largest common divisor of b and a.

That is,

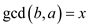[By definition of gcd]

Hence, .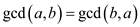

Consider the equation 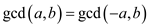to prove.

Assume that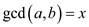. That is, x divides a and x divides b.

If x divides a, x also divides –a.

Since,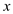divides –a and b and x is the largest common divisor of –a and b,x is the gcd of a and b.

That is,

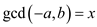[By definition of gcd]

Hence, .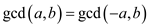

Consider the equation 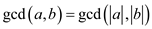to prove.

Assume that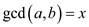. That is, x divides a and x divides b.

Even though a and b are negative values, x can divide a and b.

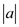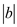That is, x can also divide and . Then .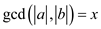

Also,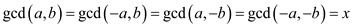

Hence,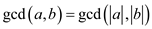

Consider the equation 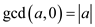to prove.

Assume that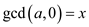. That is, x divides a and x divides 0.

Since, x divides a and 0, x can also divides a+0.

Therefore, x divides a and divides a+0, gcd(a,a+0)=x.

That is, gcd(a,0)= gcd(a,a+0)=gcd(a,a)=x.

But, gcd(a,a)=|a|. Thus, x=|a|.

Hence,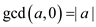

Consider the equation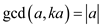 to prove.

From the important property of gcd, if d divides a and d divides b , then d also divides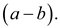

Assume that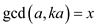. That is x divides ka and a, then x can also divide 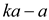or.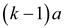

Since, x divides a and ,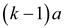

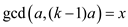
That is,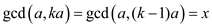

If above steps are repeated k times, the following result is obtained:

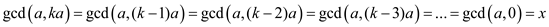
But, it is proved that 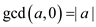. Thus, .

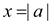Hence,.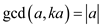

(OR)

Consider the equation .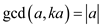

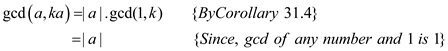
Hence, .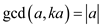

Assume that 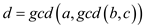------ (1)

And also assume that 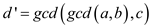------ (2)

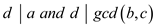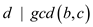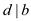Obviously . Since , also and.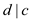

Therefore, d can divide a , b and c.

By the divisibility property, if m | x, then x can be expressed as multiple of m. That is, for some integer k.

• Since 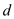is dividing a, b and c, by the divisibility property, a, b and c can be expressed as follows:

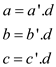
• From (2),

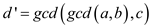
Replace the values of a,b and c in the above equation.

Thus,

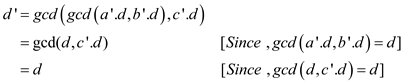
That is, 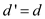------ (3)

From (1), (2) and (3) ,

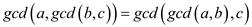
Hence it is proved that the gcd operator is associative.

The standard long division takes O(n²) time in decimal integer division as well as binary division.

Suppose the dividend is -bit integer A and divisor B is shorter in length. Following is the algorithm that shows division of A by B:

If B=0

show error message(“Division by zero exception”)

Initialize a variable Q to store the quotient, Q=0

Initialize a variable R to store the remainder, R = 0

for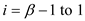

R = Left shift R by 1 bit and store into R

Set the LSB of R with i^th bit of numerator.

if (R is greater than B,) // it can divide R

R = R-D

Set i^th bit of Q to 1.

return R

Time Complexity:

The algorithm discussed above follows the Long division approach. It stores the integer bit by bit and then stores the remainder. Since the number is 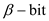in length. thus, it uses a 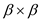matrix to store the result.

Thus, it takes 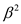time.

• Firstly, until the original number is in form of power to 2, the length of the number bumps up. Doing this will not affect the asymptotic.

• The value of the number will not be changed, if the most significant side is padded with zeros.

• Spilt the binary integer into two parts as the less and the most significant half.

• The less significant is represented by l and the most significant half is represented by m to make the input equal as .

• After that, the l and the m is converted into decimal, recursively.

• Since, there is the need of above later, then compute the decimal version of all the values of .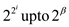

• The count of the numbers is 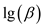, so the time taken by the straightforward approach is .

• Therefore, this will be overshadowed by the rest of the algorithm.

• After this, compute the value of , this include both addition and the multiplication of the two numbers. Therefore, the recurrence relation would be as follows:

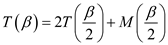
• For some value of epsilon, it is difficult to separate M from the linear by.

• The analysis become easier, if the fact that the computation for the multiplication going down in the subcases will be ignored.

As per this concession, the runtime is as follows through the master theorem:

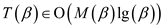
There is some procedure too to convert the binary number to the decimal. This will take only 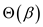time while compared with the algorithm provided by the theory of automata. This algorithm of automata takes the following time:

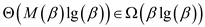
A deterministic finite transducer can be constructed between the two languages, since it will take only that number of steps as the number of bits present in the input.

This will take only linear time.

Also, keep track on the carryover from each of the digit to the next one.