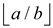First, the expressions which are given in the equation (31.13) are as follow:
They are the common divisors.

Everything that are shown above are the integer, they are not the exponents which are negative.
Now, prove that there is no longer a common divisor.
This is done by proving that for each of the prime, there is no power is higher.
Assume there is some common divisor d of a and b.
First it is known that the d consists of a prime factor which is not appear in both a or b, otherwise any of the integer times d also consist of that factor.
But being a common divisor, one can write both a and b in the form of any integer time d.
Therefore, there is some sequence which is represented
by so
that
so
that .
.
Now claim the following:
For every i, .
.
Assume to a contradiction that there was some i, therefore the following:
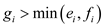
This results that the number of factors of d is more than a and b.
Since, multiplying the integers will not result to decrease the count of factors of each prime.
Therefore, this is a contradiction.
Since, the claim is that the d is a common divisor.
Since, each prime under d has the power lower than the power of the primes of c.
We should have the following:
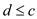
Thus, c is a greatest common divisor.
EXTENDED-EUCLID algorithm is the extension for the EUCLID algorithm. As EUCLID Algorithm, EXTENDED-EUCLID is also used to find the greatest common divisor (gcd) of two numbers. GCD of two numbers a, b can be computed as follows:

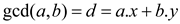
The given numbers are a=899 and b=493.
Now, the EXTENDED-EUCLID (899, 493) recursively calls the following sub problems:
EXTENDED-EUCLID (493,406)
EXTENDED-EUCLID (406,87)
EXTENDED-EUCLID (87,58)
EXTENDED-EUCLID (58,29)
EXTENDED-EUCLID (29,0)
When the algorithm calls EXTENDED-EUCLID (29,0), b is zero.
Therefore, it returns (29,1,0)
|
a |
b |
|
d |
x |
y |
|
899 |
493 |
||||
|
493 |
406 |
||||
|
406 |
87 |
||||
|
87 |
58 |
||||
|
58 |
29 |
||||
|
29 |
0 |
– |
29 |
1 |
0 |
Since EXTENDED-EUCLID (29,0) returns (29,1,0), for the call
EXTENDED-EUCLID (58,29), 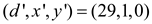
Then,
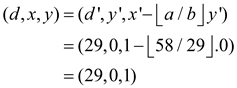
|
a |
b |
|
d |
x |
y |
|
899 |
493 |
||||
|
493 |
406 |
||||
|
406 |
87 |
||||
|
87 |
58 |
||||
|
58 |
29 |
2 |
29 |
0 |
1 |
|
29 |
0 |
– |
29 |
1 |
0 |
Since EXTENDED-EUCLID (58,29) returns (29,0,1), for the call
EXTENDED-EUCLID (87,58), 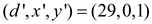
Then,
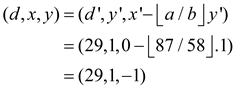
|
a |
b |
|
d |
x |
y |
|
899 |
493 |
||||
|
493 |
406 |
||||
|
406 |
87 |
||||
|
87 |
58 |
1 |
29 |
1 |
-1 |
|
58 |
29 |
2 |
29 |
0 |
1 |
|
29 |
0 |
– |
29 |
1 |
0 |
Since EXTENDED-EUCLID (87,58) returns (29,1,-1), for the call
EXTENDED-EUCLID (406,87), 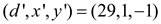
Then,
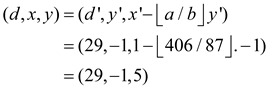
|
a |
b |
|
d |
x |
y |
|
899 |
493 |
||||
|
493 |
406 |
||||
|
406 |
87 |
4 |
29 |
-1 |
5 |
|
87 |
58 |
1 |
29 |
1 |
-1 |
|
58 |
29 |
2 |
29 |
0 |
1 |
|
29 |
0 |
– |
29 |
1 |
0 |
Since EXTENDED-EUCLID (406,87) returns (29,-1,5), for the call
EXTENDED-EUCLID (493,406), 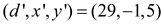
Then,
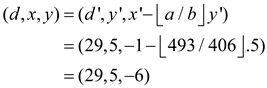
|
b |
|
d |
x |
y |
|
|
899 |
493 |
||||
|
493 |
406 |
1 |
29 |
5 |
-6 |
|
406 |
87 |
4 |
29 |
-1 |
5 |
|
87 |
58 |
1 |
29 |
1 |
-1 |
|
58 |
29 |
2 |
29 |
0 |
1 |
|
29 |
0 |
– |
29 |
1 |
0 |
Since EXTENDED-EUCLID (493,406) returns (29,5,-6), for the call
EXTENDED-EUCLID (899,493), 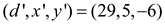
Then,
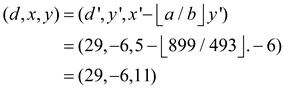
|
a |
b |
|
d |
x |
y |
|
899 |
493 |
1 |
29 |
-6 |
11 |
|
493 |
406 |
1 |
29 |
5 |
-6 |
|
406 |
87 |
4 |
29 |
-1 |
5 |
|
87 |
58 |
1 |
29 |
1 |
-1 |
|
58 |
29 |
2 |
29 |
0 |
1 |
|
29 |
0 |
– |
29 |
1 |
0 |
Finally, the call EXTENDED-EUCLID (899, 493) returns (29,-6,11).
Therefore, 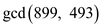
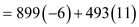 =29
=29
Consider the provided statement 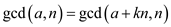 where
where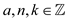 .
.
From the definition of greatest common divisor (gcd), 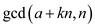 divides
divides
 and also divides
and also divides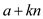 .
.
Now by the linear combination property, as 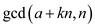 divides
divides
 ,
then
,
then 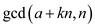 can also
divide
can also
divide 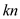
Since, 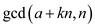 divides
divides
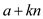 and
and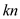 ,
, 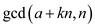 can also
divide
can also
divide 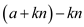
Therefore,
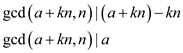
By corollary 31.3, if d | a and d | b, then d | gcd(a,b).
Since, 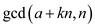 divides
a and
divides
a and 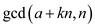 divides
n,
divides
n, 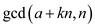 also divides
also divides
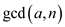 .
.
Thus,
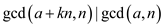 …… (1)
…… (1)
By the definition of gcd, 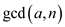 divides
a and n.
divides
a and n.
Since 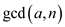 divides
n,
divides
n, 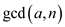 can also
divides kn.
can also
divides kn.
From the equation 31.3, if d | a and d | b, d can also divides (a+b).
Since 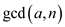 divides
a and kn,
divides
a and kn, 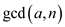 can also
divides (a+kn).
can also
divides (a+kn).
That is,
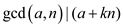
Since, 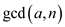 divides
(a+kn) and n ,
divides
(a+kn) and n , 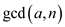 can divides
can divides
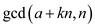
That is,
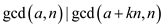 [By corollary 31.3] …… (2)
[By corollary 31.3] …… (2)
Now from equation (1) and equation (2), it can be concluded that
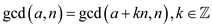
Hence, given statement is proved.
Consider the provided statement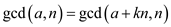 .
.
The above equation can also be proved using ECLUIDS algorithm.
According to EUCLID’s formula,
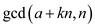 can be calculated as
can be calculated as 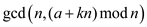
That is,
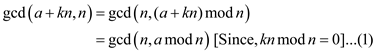
According to EUCLID’s formula,
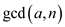 can be
calculated as
can be
calculated as 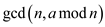
That is, 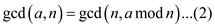
From (1) and (2), 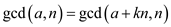
It is known that for all values of k, if the following condition is there, then the function take only fewer number of steps.
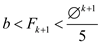
Assume the value of k to be  ,since
,since
 ,
the number of steps taken are only
,
the number of steps taken are only  .
.
The bound can be proved to be  because it
is known that the algorithm will terminate when it will reach to
because it
is known that the algorithm will terminate when it will reach to
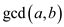 .
.
Emulate the proof of the lemma 31.10 to show a little bit
different claim that the Euclid’s take k number of recursive
calls. Then, 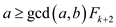 and
and
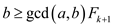 .
.
In the same way, the induction can be done for k. if the number of calls taken by k is only 1 and having a > b also the following:
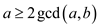 and
and
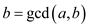
Now, assume that it can hold k-1, prove that it can holds for k.
The first call will be as 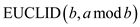 . So, this
will take only k-1 recursive calls.
. So, this
will take only k-1 recursive calls.
For the following, the induction can be applied:
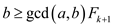 and
and 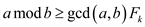
Since, there is a > b, 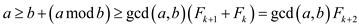 completing
the induction.
completing
the induction.
Only k number of steps are needed therefore, if 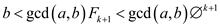 .
.
We have the following:
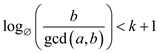
Thus, it is satisfied that the value of k will be set as follows:

Since, gcd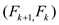 =gcd
=gcd ,
so gcd (2,1) =1. It means that gcd
,
so gcd (2,1) =1. It means that gcd for all
k.
for all
k.
Also,  is
increasing so
is
increasing so 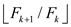 =1 for all
k. When the base case of recursive calls is reached return (1,1,0).
The procedure EXTENDED-EUCLID takes as input a pair of non-negative
integers and returns a triple of the form (d, x, y) which satisfies
=1 for all
k. When the base case of recursive calls is reached return (1,1,0).
The procedure EXTENDED-EUCLID takes as input a pair of non-negative
integers and returns a triple of the form (d, x, y) which satisfies
 .
.
The algorithm is as follows:
EXTENDED-EUCLID (x, y)
1 if y=0
2 return (x,1,0)
3 else
4 ( d ,a, b)=EXTENDED-EUCLID(y, x mod y)
5 return ((d, b, a-(x/y) *b))
For  and
and
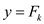 ,
,
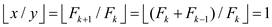 and
and 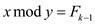 .
.
The small cases are generated in the following ways:
EXTENDED-EUCLID (1,0) returns (1,1,0).
EXTENDED-EUCLID ( ) computes
(1,1,0) and returns (1,0,1).
) computes
(1,1,0) and returns (1,0,1).
EXTENDED-EUCLID (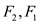 ) computes
(1,0,1) and returns (1,1, -1).
) computes
(1,0,1) and returns (1,1, -1).
and so on, the pattern emerges as:
EXTENDED-EUCLID ( .
.
The other formula is: EXTENDED-EUCLID (
Thus, the EXTENDED EUCLID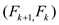 returns
returns
 .
The best case is handled by d. If the claim holds for k-1,
then EXTENDED EUCLID
.
The best case is handled by d. If the claim holds for k-1,
then EXTENDED EUCLID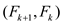 returns
returns
 where
where  =1,
=1,
 ,
,
 so
the algorithm returns.
so
the algorithm returns.

The gcd of n+1 integers can be defined by gcd function with n+1
arguments as  which can
be written in recursive form as
which can
be written in recursive form as 
The gcd operator is associative, so compute gcd in any order
 or
or
 and so on.
and so on.
To show that the gcd function returns the same answer which is independent of the order in which its arguments are specified prove the swap property which is as follows:
• For all a,b,c, gcd(a,gcd(b,c))=gcd(b,gcd(a,c))
• Apply the swaps and obtain an arbitrary ordering on the variables.
• Let  be the power
of the
be the power
of the 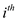 prime in the
prime factor decomposition of ‘x’, similarly define
prime in the
prime factor decomposition of ‘x’, similarly define  and
and
 .
Then, the calculation is performed as follows:
.
Then, the calculation is performed as follows:

To find the integers  as described
in the problem use a similar approach as for EXTENDED-EUCLID
algorithm such that
as described
in the problem use a similar approach as for EXTENDED-EUCLID
algorithm such that  .
.
As per the interpretation of the greatest common divisor defined in the equation (31.13), the lcm is given as follows:

Generally, the lcm would be as follows:
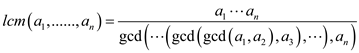
The denominator is computed recursively by the two argument gcd operation.
The algorithm is shown below:

The complexity of the above algorithm is 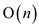 .
.
The integers n1,n2,…,nk are called as pair wise relatively prime only if the
gcd(ni, nj)= 1. For every possibility of i and j with i ≠ j.
For a complete graph, 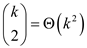
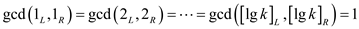 .
.
For k=2, 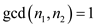
For k=3, 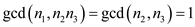
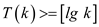 .
.
With the help of strong mathematical induction,
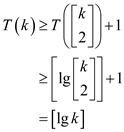
Consider the integers 3, 5, 7 and 11. These integers can be proved pair wise relative prime is as follows:
gcd(n1n2,n3n4)=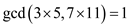
gcd(n1n3,n2n4)=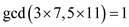
Therefore,

Hence, n1, n2, n3, and
n4 are pair wise relatively prime if and only if
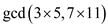 =
=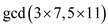 =1 has been
proved successfully.
=1 has been
proved successfully.