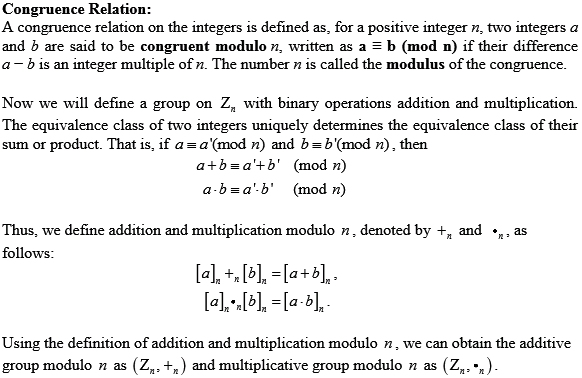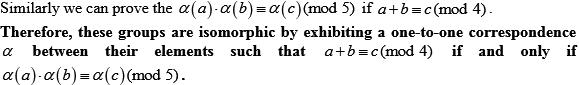Finding subgroup of 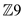 :
:
Consider the group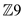 ={0,1,2,3,4,5,6,7}.
={0,1,2,3,4,5,6,7}.
• The total number of subgroup of a group is equal to the total
number of divisor. So the divisors of 9 are 1, 3 and 9 itself.
Therefore, the total number of subgroups of a group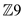 is equal to
3.
is equal to
3.
• It is known that every group has two trivial subgroups which
are zero and itself. So, the first two trivial subgroups of
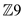 are
given as:
are
given as:

• Sub groups for 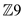 can be
generated using
can be
generated using 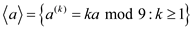

• Sub group generated by 0:
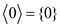
• Sub group generated by 1:
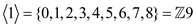
• Sub group generated by 3:
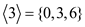
Hence, the subgroups of 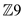 are
are 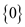 ,
, 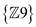 and
and 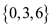 .
.
Finding subgroups of 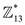 :
:
Consider the group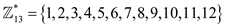 .
.
• Here, 13 is a prime number. Therefore, the subgroup of
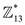 is
same as
is
same as . That is
. That is
 .
.
• The total number of subgroup of a group is equal to the total
number of divisor. So the divisor of 12 are 1, 2, 3, 4, 6 and 12
itself. Therefore, the total number of subgroup of a group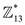 is equal to
6.
is equal to
6.
• Now, calculate the power of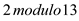 , which are
given below:
, which are
given below:
• 
• Therefore,  is cyclic of
order 12, with a generator 2.
is cyclic of
order 12, with a generator 2.
Thus the sub groups of 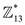 are
are
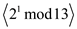 ,
,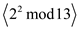 ,
,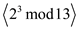 ,
,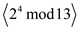 ,
,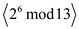 and
and 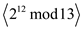
• Sub groups for 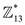 can be
generated using
can be
generated using 
• Sub group generated by 1:
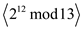 =
=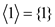
• Sub group generated by 2:
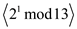 =
=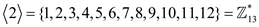
• Sub group generated by 3:
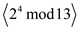 =
=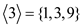
• Sub group generated by 4:
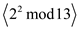 =
=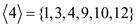
• Sub group generated by 8:
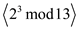 =
=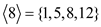
• Sub group generated by 12:
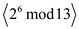 =
=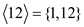
Hence, the subgroups of 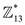 are
are 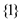 ,
, 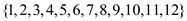 ,
, 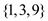 ,
, 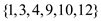 ,
,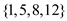 and
and
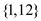 .
.
To prove that a non-empty closed subset of a finite group is a
subgroup the following properties of the group 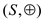 where S is
the set and
where S is
the set and  is the
binary operation must hold:
is the
binary operation must hold:
• Closure.
• Identity.
• Associativity.
• Inverse.
To prove that a non-empty closed subset (let it is denoted by H) of a finite group (let it is denoted by G) is a subgroup, the above-mentioned properties are satisfied in the following way:
Closure: Suppose H is the non-empty closed subset of a
finite group G. It should be proved that H is a sub-group. Since H
is closed, so it follows the condition that if 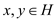 , then
, then
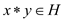 .Thus, the
subset is closed.
.Thus, the
subset is closed.
Identity: Since S is a finite group, every element had a
finite order so, if  there is
some number of times that can be added to itself so that the
identity can be obtained. So, adding any two things in
there is
some number of times that can be added to itself so that the
identity can be obtained. So, adding any two things in  helps to get
something in
helps to get
something in  . Suppose
. Suppose
 then
then
 .
Since, the subset is finite, there must be a condition such that
.
Since, the subset is finite, there must be a condition such that
 .
Hence,
.
Hence, 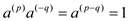 and
therefore the subset must contain the identity.
and
therefore the subset must contain the identity.
Associativity: The associativity is inherited from the
group because  is a
property of binary operation.
is a
property of binary operation.
Inverse: Suppose 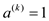 , the
inverse of the element ‘a’ is
, the
inverse of the element ‘a’ is 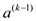 as
as 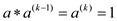 . Thus, the
inverse of every element is contained within itself because the
element is added to itself several times equal to one less than its
order.
. Thus, the
inverse of every element is contained within itself because the
element is added to itself several times equal to one less than its
order.
Permutation: A mapping 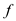 is define
to be a permutation if the mapping is one-one and onto and define
from same set to same set.
is define
to be a permutation if the mapping is one-one and onto and define
from same set to same set.
That is if 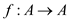 such that
such that
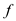 is
one-one and onto than
is
one-one and onto than 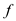 is said to
be a permutation on
is said to
be a permutation on 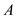
Consider a mapping

Such that
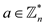
Here,

Define as
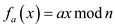 ……(1)
……(1)
Suppose,
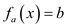
Then (1) can be rewritten as

To Prove:  is
one-one
is
one-one
Suppose,
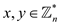
Consider,
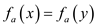 ……. (2)
……. (2)
Suppose,
 …… (3)
…… (3)
And
 ……. (4)
……. (4)
Substitute (3) and (4) in (2)
 …… (5)
…… (5)
Here, 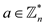 and with
reference to the theorem 31.13 it can say that
and with
reference to the theorem 31.13 it can say that  is a finite
abelian group thus it can say that the inverse of
is a finite
abelian group thus it can say that the inverse of 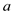 will exist
in
will exist
in  . Let
. Let
 denote the inverse of
denote the inverse of 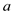 in
in
 that is
that is
 …… (6)
…… (6)
Pre multiply both side of (5) by 
 …… (7)
…… (7)
Apply (6) in (7)

Thus,

Hence, it can say that the function  is
one-one.
is
one-one.
To Prove:  is onto
is onto
Suppose,
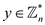
Such that
 …… (8)
…… (8)
The equation (8) can be rewritten as
 …… (9)
…… (9)
Here, 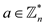 and with
reference to the theorem 31.13 it can say that
and with
reference to the theorem 31.13 it can say that  is a finite
abelian group thus it can say that the inverse of
is a finite
abelian group thus it can say that the inverse of 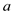 will exist
in
will exist
in  . Suppose
. Suppose
 denote the inverse of
denote the inverse of 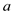 in
in
 that is
that is
 …… (10)
…… (10)
Pre multiply both side of (9) by 
 …… (11)
…… (11)
As  and
and
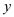 belongs to
belongs to  and
and
 is
a finite abelian group therefore
is
a finite abelian group therefore .
.
Thus, 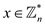 .
.


Thus for each 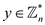 there exist
there exist
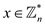 such that
such that
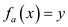
Hence, it can say that the function  is
onto.
is
onto.
The function  is both
one-one and onto. Therefore, by the definition of permutation, it
can say that
is both
one-one and onto. Therefore, by the definition of permutation, it
can say that 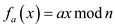 is
permutation of
is
permutation of  .
.