Consider, if 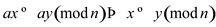 .
.
Now, prove that 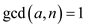 .
.
It is provided that 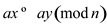
The above equation states that 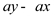 is
divisible by
is
divisible by 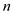 . It can be
represented as follows:
. It can be
represented as follows:
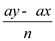
There exists some integer 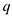 where
where
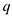 is
said to be the quotient such that,
is
said to be the quotient such that,
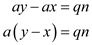
From the above statement, it concludes that 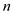 divides
divides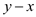 .
.
It is provided that 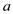 and
and
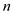 are relatively prime. So,
are relatively prime. So, 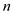 cannot
divides
cannot
divides 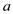 . That
is,
. That
is,
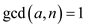
Therefore, 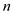 divides
divides
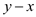
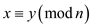
Hence, the equation 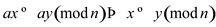 whenever
whenever
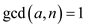 is
proved.
is
proved.
The counter example to prove 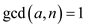 is
necessary and it is provided as follows:
is
necessary and it is provided as follows:
Assume that 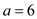 and
and
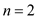 .
.
Now, calculate the greatest common divisor of 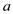 and
and
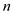 as
below:
as
below:
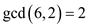
It is known that 2 is greater than 1 and it satisfies that the given condition.
Put the value of 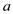 and
n in equation
and
n in equation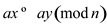 .
.
Therefore, 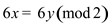
It can be said that, 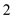 divides
divides
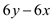 that is
that is 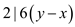 .
.
Now, from the property of division and GCD, 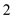 divides
divides
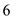 and
and 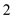 also
divides
also
divides 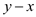 which will
be depend on the value of
which will
be depend on the value of 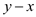 which may be
true or not.
which may be
true or not.
But if 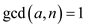 , then
, then
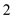 must
divides
must
divides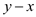 .
.
Therefore, it is necessary that 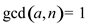 for
for
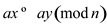 to
imply
to
imply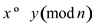 .
.
Hence given statement is proved.
The procedure MODULAR–LINEAR–EQUATION–SOLVER (a, b, n) is used to solve the modular linear equation. Refer chapter 31, section 31.4 of the text book for the complete algorithm.
Consider the line 3 of the procedure MODULAR–LINEAR–EQUATION–SOLVER (a, b, n) is replaced with the following line:
3 
The procedure MODULAR–LINEAR–EQUATION–SOLVER(a, b, n) still works even if the line 3 is replaced with the above line.
The for loop in line 5 helps in maintaining the consistency of the procedure. It will neutralize the effect of changing the line 3 and iterate till the required solution. The iterative step finds the actual solution.
For example, consider the following equation:
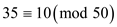
The procedure MODULAR–LINEAR–EQUATION–SOLVER(10, 35, 50) will generate the numbers 46, 6, 16, 26, 36 as output, before replacing the line 3.
Now, consider the procedure MODULAR–LINEAR–EQUATION–SOLVER(10, 35, 50) after replacing the line 3.
The procedure EXTENDED–EUCLID (50, 35) in line 1 returns 5, -2,
and 3 and they will be stored in 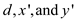 respectively. That is,
respectively. That is, 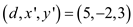 .
.
The value of  in line 3 is
calculated as follows:
in line 3 is
calculated as follows:
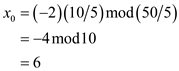
The for loop in line 4 iterates 5 times from 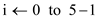 . It
computes and prints the value of
. It
computes and prints the value of 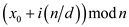 .
.
The calculations are performed and output is generated as follows:
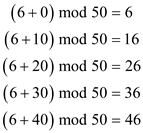
Hence, the procedure after replacing line 3 in the procedure MODULAR–LINEAR–EQUATION–SOLVER(10, 35, 50) generates 6, 16, 26, 36, 46 as output.
Therefore, the output generated by the procedure before and after replacing the line 3 is the same.
Polynomial congruence:
Consider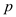 is prime and
a polynomial
is prime and
a polynomial  of degree
t. The polynomial
of degree
t. The polynomial  is given
below:
is given
below:
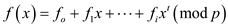
The coefficients  is obtained
from the
is obtained
from the  and
satisfies the condition
and
satisfies the condition 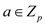 is equal to
zero of
is equal to
zero of 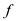 if
if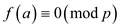 .
.
Consider p is not a prime.
Then the prime factorization of p is possible. The polynomial should be solved for following cases:

In the cases given above,  are the
factors of prime numbers and
are the
factors of prime numbers and 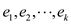 represents
their respective powers. Suppose the value of p is 175, then
the factors will be 5, 5 and 7. This leads to finding solutions for
5, 7 and 25.
represents
their respective powers. Suppose the value of p is 175, then
the factors will be 5, 5 and 7. This leads to finding solutions for
5, 7 and 25.
Now prove that if a is a zero of f , then
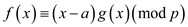
for some polynomial 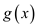 of degree
of degree
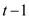 .
.
Since a is a zero of f
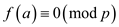 .
.
also,
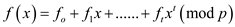 .
.
Calculate 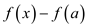 .
.
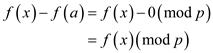
also,

Thus,

where 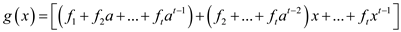
That is, 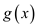 is a
polynomial of degree
is a
polynomial of degree 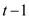 .
.
Now, use mathematical induction on t.
Base step:
Consider 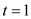 , then
polynomial
, then
polynomial 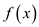 will be of
the following form:
will be of
the following form:
 .
.
To find the solution of above polynomial of degree one,
use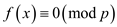

Since p is a prime,  . It is
because only 1 will be single number which is a multiple of
f1 and p.
. It is
because only 1 will be single number which is a multiple of
f1 and p.
If  , then the
linear congruence
, then the
linear congruence  always has
a unique solution, otherwise the number of solutions are determined
with the use of g|b for equation
always has
a unique solution, otherwise the number of solutions are determined
with the use of g|b for equation 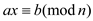 , where
g is gcd(a, n).
, where
g is gcd(a, n).
Hence, the result holds for 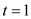 .
.
Assumption step:
Assume that this result is true for the polynomial of degree t – 1.
Induction step:
Now use the above result for t – 1 to prove this result for polynomial of degree t.
The following congruence 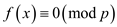 either has
no solution or at least one solution.
either has
no solution or at least one solution.
If it has no solution then there is nothing to prove.
From the above result, if a is a zero of f , then
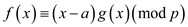
for some polynomial 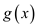 of degree
of degree
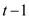 .
.
If b is another solution out of the incongruent solutions
of 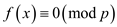 , then
, then
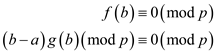
Since b is incongruent to a.
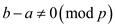
So,
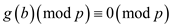
Thus, any solution of 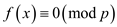 which is
different from a also satisfy
which is
different from a also satisfy
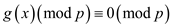
where g(x) is a polynomial of degree t – 1
By assumption, the polynomial of degree t – 1 has at most t – 1 incongruent solution.
So, the congruence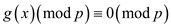 has at most
t – 1 incongruent solution.
has at most
t – 1 incongruent solution.
Hence, the congruence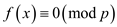 has at most
n incongruent solutions.
has at most
n incongruent solutions.
Therefore, if p is prime, then a polynomial 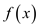 of degree
t can have at most t distinct zeros modulo
p.
of degree
t can have at most t distinct zeros modulo
p.
