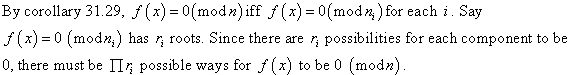Consider the following equations:
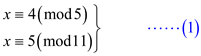
The values 5 and 11 are relatively prime to each other.
Apply the Chinese remainder theorem to find the solutions to the equations (1).
Refer chapter 31, section 31.5, theorem 31.27 of textbook for Chinese remainder theorem.
Calculate the values of s and t, such that
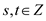and 
.
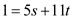Use random value substitution method to find the values of s and t.
Choose s = 20 and t = – 9.
So, the s = 20 and t = – 9 values satisfies the equation
.
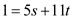Now, calculate the value of 
as
below:
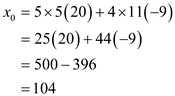
Then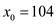 
is a
special solution of the simultaneous congruence equations 
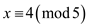and
.
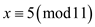Therefore, the general solution is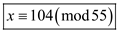 
.
Consider x is an integer such that, it leaves 1, 2, and 3 as remainders when divided by 9, 8, and 7 respectively.
x satisfies the following equations:
9 is relatively prime to 8, 8 is relatively prime to 7, and 9 is relatively prime to 7. So, the values 9, 8, and 7 are relatively prime pairs (the pairs are (9,8), (8,7), and (9,7)).
Consider the equations (1) and (2).
Apply the Chinese remainder theorem to find the solutions to the equations (1) and (2) as 9 and 8 are relatively prime.
(Refer chapter 31, section 31.5, theorem 31.27 of textbook for Chinese remainder theorem.)
Calculate the values of s and t, such that
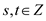and 
.
Use random value substitution method to find the values of s and t.
Choose s = 1 and t = –1.
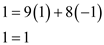
So, the values s = 1 and t = –1 satisfies the equation
.
Now, calculate the value of as
below:
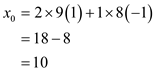
Then, 
is a
special solution of the simultaneous congruence equations 
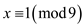and
.
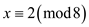Hence, the general solution of these two congruencies (1) and
(2) is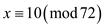 
.
Now, solve the two simultaneous congruencies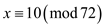 
and
equation in (3) using Chinese remainder theorem.
Calculate the values of s and t, such that
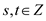and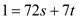 
.
Use random value substitution method to find the values of s and t.
Choose s = –3 and t = 31.
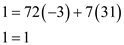
So, the values s = –3 and t = 31 satisfies the equation
.
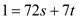Now calculate the value of as
below:
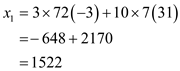
Then,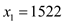 
is a
special solution of the simultaneous congruence equations 
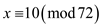and
.
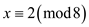The general solution of these two congruencies is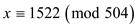 
.
Hence, the general solution of the three congruencies in (1),
(2), and (3) is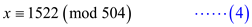 
Calculate the value of x using the equation (4).
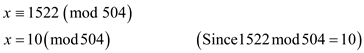
Then x can be written as follows:
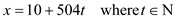
That is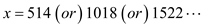 
Therefore, the integers of the form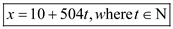 
leave remainders 1, 2, and 3 when divided by 9, 8, and 7
respectively.
Consider a set,
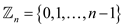
Here,
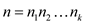
Such that 
are
pairwise relatively prime.
Consider,
Consider a one-to-one correspondence mapping define from
to
.
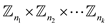…… (1)
Here, 
respectively.
Similarly for 
the mapping
(1) can be define as
Such that 
Consider,
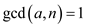
Therefore,
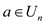
As 
form the
finite abelion group with respect to multiplication and 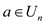thus it can
be said that the inverse of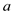 
say
will belong to.
Thus,
Define,
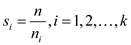
That is
Therefore,
Define,
…… (2)
As therefore
with reference to the corollary 31.26 it can say that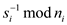 
thus the
expression (2) is well define.
Write as a
function of 
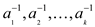as
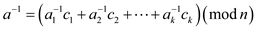
For 
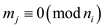
Which implies,
And
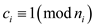
Thus,
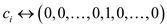
Here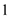 
is at the
ith position.
Consider,
As
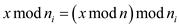
Therefore,
Thus,
Hence, Proved
