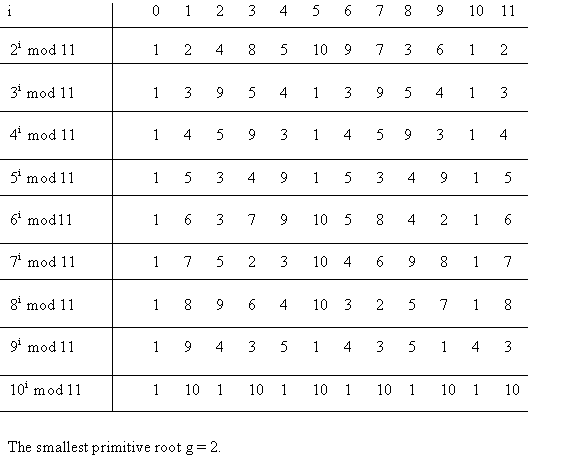
Consider the following modular exponential algorithm, in which the bits of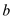are examined from right to left.

Algorithm:

//Define the procedure modular exponential which takes

//three argument as an input

DEF–RL–MODULAR–EXPANSION (a, b, n)

//Initialize a variable p with 1

1 p=1

//use while loop with condition always true or

// this while loop will always execute

2 while 1:

//now takes the modulus of b with 2 and if the result is

//equal to 1 then execute if condition

3 if (b mod 2) ==1:

//calculate the modular expansion

4 p = (p.a) mod n

//now perform division operation

5 b=b/2

//check the value of b, if b==0 then breaks or come outside the loop

6 if b==0:

//perform break operation

7 break

//if b!=0 then perform the following operation

8 a=(a.a)modn

//at the end returns the value of p

9 return p

The above given algorithm reduce every multiplication (mod n). Hence, the above algorithm is useful for small numbers instead of the large numbers.

For small numbers, the above right to left modular exponential algorithm is somewhat faster than the left to right exponential algorithm.

Implementation of MODULAR EXPONENTIATION

For any integer n.

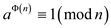for any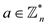

Algorithm for computing.

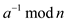for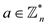using the procedure of MODULAR-EXPONENTIATION.

Modular exponentiation:

The modular exponentiation is a kind of exponentiation that is applied on the modulus of a number. It has various applications in network security. This method is used to calculate the power to a number using repeated squaring rather than multiplying the number by itself several times. It can be represented as: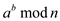

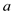Where, and b are positive integers and n contains a positive value. In the repeated squaring process, use the binary representation of b that is k bit long binary value of b.

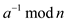In the calculation ofcan be done if preliminarily the condition of power of 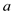is checked and the value of 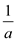for its negative value is returned.

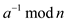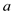For calculating, and n both should be co-prime. Use the procedure of MODULAR-EXPONENTIATION by editing it for the calculation of 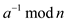which is as:

The procedure below calculates the modular exponentiation of the equation of the form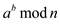 where both of 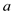and b are non-negative numbers and the numbern is a positive integer.

MODULAR-EXPONENTIATION(a, b, n)

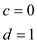
if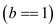

return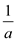

// for each binary value of b

for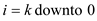

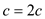
// squaring d and then calculating modular value

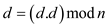
if

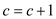
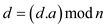
return d

Example:

Consider

Multiplying a on both side

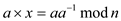
Now,

Now, according to the Fermat theorem (here n is prime),

And

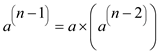
It means that 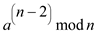is the solution.

Example: Assume that.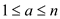

Let 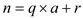be the division with remainder of.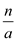

To prove that the algorithm given above is correct,

Consider

.

As gcd(7,9) is 1.

So,

9 will be divided in pair of 7.

This is given below:

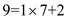
Now, 7 will be divided in pairs and it is given below:

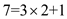
Now, taking 3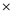2 to left side, the equation will become as:

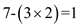
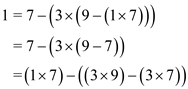
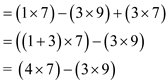
So, the inverse of ‘7 mod 9’ is 4 because 4 pair of 7 is used here.

In this process of this MODULAR-EXPONENTIATION first check the power of 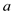and change it accordingly if it is not negative and then proceed to next step. Thus this procedure calculates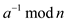.