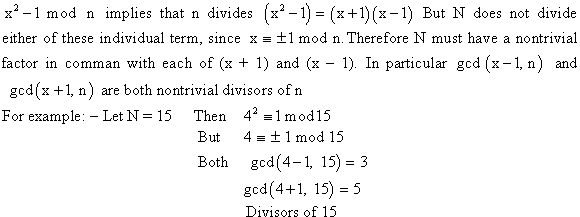Euler’s Theorem
Euler’s theorem is used to reducing the large powers modulus
n. Suppose it is given that 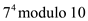 is equal to
1 and the value of
is equal to
1 and the value of 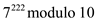 should be
calculated. According to Euler’s theorem,
should be
calculated. According to Euler’s theorem, 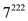 can also be
written as
can also be
written as . This
equation will become
. This
equation will become . This can
also be written as:
. This can
also be written as: 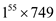 modulo 10.
So, answer will be 9.
modulo 10.
So, answer will be 9.
This Euler’s theorem can also be strengthened. For strengthening Euler’s theorem, consider the form given below:
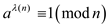
Where 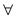
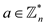 ,
,  and
and

Carmichael numbers: Carmichael numbers are those numbers which are composite but when Fermat’s primality test is applied on them, they pass the test. According to Fermat primarily test; a number is prime if it satisfies following condition:
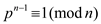
Where 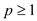 and
and
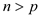
This can also be written as:
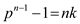
Where k is a positive integer.
Proof of 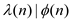 : Let
: Let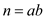 , where
a is a prime number, it is found that
, where
a is a prime number, it is found that 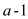 can divide
can divide
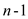 only if it can divide
only if it can divide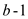 .
Subtracting b from left hand side and right hand side, the
equation
.
Subtracting b from left hand side and right hand side, the
equation 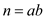 can also be
written as:
can also be
written as:
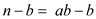
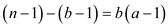
So, 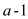 divides
divides
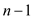 if
and only if it divides
if
and only if it divides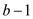 . This
proves that
. This
proves that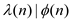 .
.
Carmichael numbers are the product of at-least three prime numbers: Consider a Carmichael number n which is product of two prime factors a and b. It is given below:
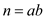
Where a and b are both prime numbers and the value
of 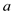 is greater than
is greater than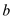 . This can
also be written as:
. This can
also be written as:
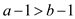
As the value of a is greater than b then it cannot
divide b, there must exist one another prime number
c, so that 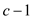 should be
divided by
should be
divided by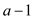 . So,
n cannot be said to be a Carmichael number until it has
three prime numbers. It must be product of at least three prime
numbers.
. So,
n cannot be said to be a Carmichael number until it has
three prime numbers. It must be product of at least three prime
numbers.
Square free numbers: A number as square free if it is prime factorization do not contain the repeated factors. In other words the number should not be divisible by a number which is a square of another number except 1.
For example 14 is a square-free number because 14 can be obtained by multiplying 2 and 7 or vice-versa while 18 is not a square-free as it is obtained by 2, 3 and 3 which contains 3 twice in it. The examples of square-free numbers are 1, 2, 3, 5, 6, 7, 10, 11, 13 …… and so on.
Carmichael numbers are square free numbers: Consider that n is a number and it is non square free. So, it can be written as:

Where the number p is a prime number, the value of
r is in integer form, value of k is taken in such a
manner that the value of k will be always greater than or
equal to 2 and 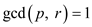 .Here, the
value of p is taken in such a manner that it satisfies the
condition
.Here, the
value of p is taken in such a manner that it satisfies the
condition . So, the
value of r will be
. So, the
value of r will be 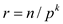 and this is
a co-prime to p.
and this is
a co-prime to p.
Using Binomial theorem and use of conditions  and
and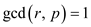 ,
,
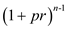 can also be written as:
can also be written as:
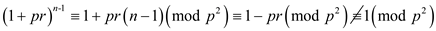
Let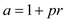 , as it is
found that
, as it is
found that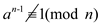 .
So,
.
So,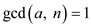 . This means
that n is not a Carmichael number. Hence, Carmichael numbers
are always square free numbers.
. This means
that n is not a Carmichael number. Hence, Carmichael numbers
are always square free numbers.