Consider the provided value of p and q for
text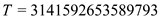 .
.
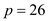 And
And 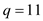
The number of digits in p is 2 therefore window size m becomes 2.
Assume x is the remainder.
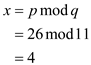
• A spurious hit will occur when p has a value, such that
the value of 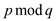 is 4.
is 4.
• A proper match will occur when remainder is 4 and p is 26.
Now, each time extract two digits from the text T, and match as follows.
|
Different (p) |
Remainder (p mod q) |
Status |
|
|
p1 |
31(first two digits of T) |
9 |
No Hit |
|
p2 |
14(2nd and 3rd digits of T) |
3 |
No Hit |
|
p3 |
41 |
8 |
No Hit |
|
p4 |
15 |
4 |
Spurious Hit |
|
p5 |
59 |
4 |
Spurious Hit |
|
p6 |
92 |
4 |
Spurious Hit |
|
p7 |
26 |
4 |
Proper Match |
|
p8 |
65 |
10 |
No Hit |
|
p9 |
53 |
9 |
No Hit |
|
p10 |
35 |
2 |
No Hit |
|
p11 |
58 |
3 |
No Hit |
|
p12 |
89 |
1 |
No Hit |
|
p13 |
97 |
9 |
No Hit |
|
p14 |
79 |
2 |
No Hit |
|
p15 |
93 |
5 |
No Hit |
Observe the above table, the remainder is 4 is obtained, when p is 15, 59, 92, and 26. When the value of p is 26, the match is a proper match, but not a Spurious Hit.
Therefore, the numbers of Spurious Hits are 3 .
A RABIN-KARP-MATCHER method is used to determine the P pattern in text string T. Make following modification in Rabin-Karp method to determine any one pattern among K patterns:
Suppose P is a 2-D array which contains K patterns. Each pattern of P is m characters long.
FIXED-RABIN-KARP-MATCHER (T, P, d, q, K)
//determine the length of first pattern of P. The length of all pattern in P are same.
1 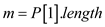
2 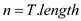
//loop used to check all pattern in P till one pattern is not found
3 for 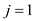 to
to
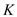
4 
5 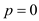
6 
//use for loop to determine the hash value of jth pattern and text strings T.
7 for 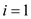 to
to
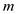
8 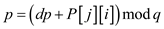
9 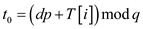
//use for loop to traverse the whole text strings T.
10 for 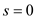 to
to
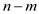
//compare the hash value.
11 if 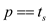
//check whole pattern matches
12 if 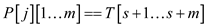
13 print “jth pattern occur with shift” s
//control moves to the calling function after finding one
// pattern of P in text string T
14 return
//recalculate the hash value
15 if 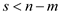
16 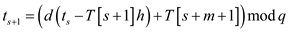
Modification for fixed pattern:
• All K pattern has same length, so determine the first pattern length.
• Use one more for loop in line 3 to traverse all K pattern till one pattern is not found in text string T.
• Make modification in 8th and 12th line
to replace 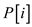 and
and
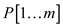 with
with
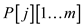 and
and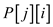 .
.
• Add return statement in 14th line to return the control when one pattern is found.
Modification required for variable patterns:
Only small modification in FIXED-RABIN-KARP-MATCHER is required for variable K patterns. For variable K patterns put 1st line code inside the first for loop. The first 4 line after modification in FIXED-RABIN-KARP-MATCHER are as follow:
VARIABLE-RABIN-KARP-MATCHER (T, P, d, q, K)
//determine the length of text string T.
1. 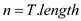
//loop used to check all pattern in P till one pattern is not found
2. for 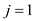 to
to
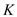
//determine the length of jth pattern.
3. 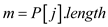
4. 
Rest all code from line 5 to 16 will be same as above FIXED-RABIN-KARP-MATCHER algorithm.
Make following modification to determine 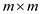 ‘P’
pattern in
‘P’
pattern in 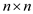 ‘T’
character array.
‘T’
character array.
• One of the best methods is to get first row from pattern P and check that pattern in first row of character array T.
• If pattern is found then fetched second pattern from P again find that pattern from first row of character array T.
• When pattern is not found in first row of character array T then find that pattern in second row of character array T and so on. If pattern is not found in any row of T array then return text NOT FOUND.
Consider the following CHECK algorithm to determine 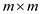 ‘P’
pattern in
‘P’
pattern in 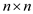 ‘T’
character array.
‘T’
character array.
CHECK 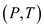
//use nested for loop to check each row of P and T.
1 for 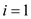 to
m
to
m
2 for 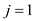 to
n
to
n
//call function to check particular ith row exist in jth row of T
3 if RABINKARP 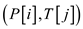 != NOT
FOUND
!= NOT
FOUND
4 break
//use if statement to check particular ith row does not exist in T.
5 if 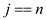
6 break
7 return NOT FOUND
//function to check pattern exist in text or not
RABINKARP 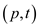
//calculate the hash value
1 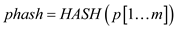
2 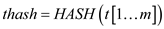
//use loop to check the pattern in t
3 for 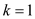 to
to
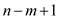
//compare the hash value
4 if 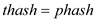
5 if 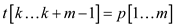
6 return k
7 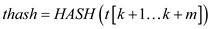
8 return NOT FOUND
Time complexity:
• In above CHECK algorithm a nested for loop is used to
check 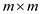 ‘P’
pattern in
‘P’
pattern in 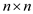 ‘T’.
‘T’.
• In each iteration of nested for loop a RABINKARP function is called which also uses one for loop.
Hence, the total time complexity of CHECK algorithm to determine
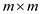 ‘P’ pattern in
‘P’ pattern in  ‘T’
character array is
‘T’
character array is .
.
ALICE AND BOB
Alice and Bob are the two names of person who communicates with each other. In computer language, it is easy for them to communicate, it is because their desired conditions are represented by 1 are non-desired conditions are represented by 0. After this, an algorithm is used that tests the conditions and returns whether there exists condition when desired conditions of both are matched or not.
Most commonly used method is matrix method, where all the conditions are shown and at desired positions 1 will be there. Suppose the bit transferred by Alice is represented by ‘red’ and bits of Bob is represented by ‘blue’, the corresponding matrix can be shown as:
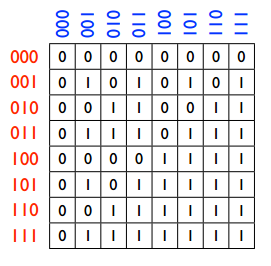
Matrix
In the given problem, Alice has a copy of n-bit file
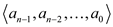 and in the same way, the Bob has an n-bit file as
and in the same way, the Bob has an n-bit file as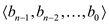 . Both Alice
and Bob wants to check whether the files that both have are
identical or not. And in the process of file transmission they use
the concept of probability for the file checking.
. Both Alice
and Bob wants to check whether the files that both have are
identical or not. And in the process of file transmission they use
the concept of probability for the file checking.
In order to check whether both files are same, Alice can send the whole file to Bob and the Bob checks both files and return ‘Yes’ if both files are same otherwise ‘No’. This method is very costly and time taking. One another method for checking whether both files are same is given below:
A prime q is selected in the process in such a way that
an integer x which is obtained from the set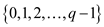 . The value
of q is selected in such a manner that
. The value
of q is selected in such a manner that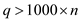
Suppose that the bits that Alice have are represented by A and
bits that Bob has are represented by B. Here, the functions are
used for fits are their corresponding functions are represented by
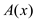 and
and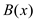 . Using this
condition, the function
. Using this
condition, the function 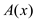 is
evaluated by Alice which is as below:
is
evaluated by Alice which is as below:

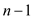 . The same
procedure is followed by the bob in which the function
. The same
procedure is followed by the bob in which the function  is
evaluated. The function is given below:
is
evaluated. The function is given below:
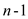 .
.As it is known that a belongs to Zq
provides a zero of given polynomial 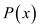 and
if
and
if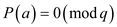 ,
then the polynomial
,
then the polynomial 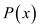 has maximum
of n distinct zeros. To prove the required condition as
stated in the problem, it is checked that both Alice and Bob sends
has maximum
of n distinct zeros. To prove the required condition as
stated in the problem, it is checked that both Alice and Bob sends
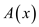 and
and  respectively.
respectively.
So, if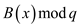 , and since
, and since
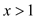 then
then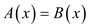 , then it
can be concluded that
, then it
can be concluded that 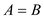 and thus,
the integer
and thus,
the integer 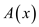 would take
more than n-bits to send. Hence,
would take
more than n-bits to send. Hence, 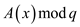 and
and
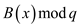 are evaluated.
are evaluated.
Here, the value of q is taken greater than 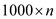 and the
value of x is chosen between 0 to
and the
value of x is chosen between 0 to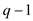 . So, if the
value of both the evaluations does not match, then there will be
one case when the value can be the same.
. So, if the
value of both the evaluations does not match, then there will be
one case when the value can be the same.
Consider an example in which the length of bits is 4 bit:
Consider that Alice has a file in which bits are {1, 0, 0, 1} and
Bob has a file containing bits {0, 1, 0, 1}. So, the value of
n is 4. Now, a value of q is selected in such a manner that
it should satisfy the condition 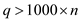 and also a
prime. This means that a prime number is selected having prime
value greater than 4000. The prime values greater than 4000 are
4001, 4003, 4007 and so on.
and also a
prime. This means that a prime number is selected having prime
value greater than 4000. The prime values greater than 4000 are
4001, 4003, 4007 and so on.
After selecting the value of q as 4001, the value of
x should be selected. The value of x lies between 0
to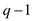 ,
any value which lies from 0 to 4001 can be taken into
consideration. Select the value of x as 2.
,
any value which lies from 0 to 4001 can be taken into
consideration. Select the value of x as 2.
Now, the functions 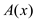 and
and
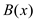 are calculated. This can be given as:
are calculated. This can be given as:
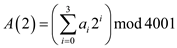
After expansion, the equation can also be written as:

Now, insert the value of a0 to a3, the equation given above becomes:
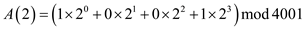
As, the a0 and a3 has values 1, so their corresponding values can be written as:
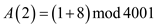
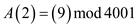
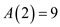
Similarly, the value of 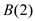 can be
calculated as:
can be
calculated as:

After expansion, the equation of 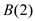 can also be
written as:
can also be
written as:

Now, on putting the values of b0 to b3, the above equation becomes:
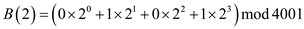
As, the b1 and b3 has values 1, so their corresponding values can be written as:
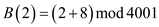
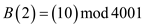
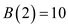
As, the value of functions 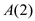 and
and
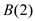 are different, this states that the bits are different.
are different, this states that the bits are different.
Here, the number of roots of the polynomial are checked over the
field and by using the condition that if 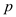 is a prime
such that
is a prime
such that 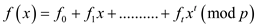 is the
polynomial of degree t in which
is the
polynomial of degree t in which  is obtained
from
is obtained
from . So as
. So as
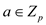 is
zero, if
is
zero, if 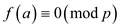 then if
a is zero of
then if
a is zero of 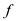 then
then
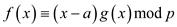 for a polynomial
for a polynomial 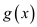 of
degree
of
degree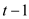 . Hence, if
p is a prime, then polynomial
. Hence, if
p is a prime, then polynomial 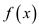 of degree
t can have at most t distinct zeros modulo p.
The probability can be found by using the equation given below:
of degree
t can have at most t distinct zeros modulo p.
The probability can be found by using the equation given below:
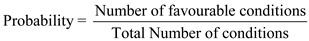
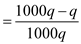
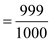
So, the probability will be:
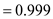
This means that if the value of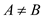 , and then
there will be one chance among 1000 chances that
, and then
there will be one chance among 1000 chances that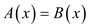 . It is
clear from the values of functions
. It is
clear from the values of functions 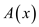 and
and
 that if their values are same then the value of A will be
equal to B.
that if their values are same then the value of A will be
equal to B.