Refer to the circuit given in figure 34.8(b) of the text book.
Verifying that the circuit is unsatisfiable requires the following steps to be followed:
• Find out the Boolean formula or the expression for the output of the circuit diagram.
• Reduce the expression further to make the observations easier.
• Draw truth table for every possible input values for the circuit and derive the output.
Then using the truth table, it is found out whether the circuit is unsatisfiable.
Satisfiability: It refers to whether an interpretation exists according to which the value of the Boolean formula becomes TRUE.
In other words, it means whether a combination of possible truth values of the variables can make the Boolean formula give TRUE as the output. The absence of such an interpretation is called unsatisfiable.
Finding out the Boolean expression for the circuit diagram:
The Boolean expression for the circuit diagram can be done by individually observing each segment of the circuit diagram and then combining these observations together appropriately.
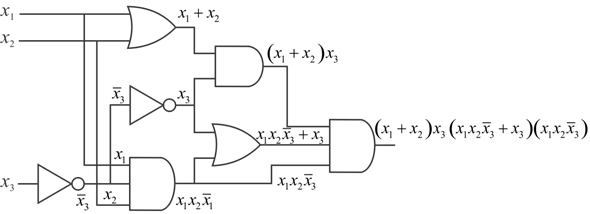
On individually observing each segment and combining according to the function of the GATES, the output expression that is obtained is the following:

The above is the output expression for the circuit diagram.
Reducing the output expression:
The output expression can be reduced by using the various Boolean laws and theorems as follows:


As it can be seen from the reduced expression of the output expression, the output always holds 0 (or FALSE) as the value.
So, there are no interpretations according to which the Boolean circuit gives TRUE value as output. The output of this circuit diagram is always FALSE. Therefore, drawing the truth value table is not needed anymore as the output remains FALSE constantly for any combination of input values.
Thus, it is proved that the circuit diagram is unsatisfiable.
Consider a polynomial-time reduction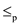 . The
polynomial-time reduction
. The
polynomial-time reduction  means,
“there exists a computable function
means,
“there exists a computable function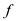 : alphabet
of L
: alphabet
of L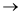 alphabet of
M in such a way that for all
alphabet of
M in such a way that for all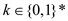 ,
, 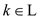 if and only
if
if and only
if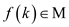 ”.
”.
Proving 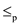 relation is a transitive relation:
relation is a transitive relation:
• Consider two polynomial-time reductions  and
and . In other
words, there exists a polynomial-time computable reduction
functions
. In other
words, there exists a polynomial-time computable reduction
functions and
and in
such a way that :
in
such a way that :
 …… (1)
…… (1)
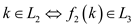 …… (2)
…… (2)
• Now, define a function 
 such that,
such that,
 .
.
Now, it is enough to prove that  is
polynomial-time reducible to
is
polynomial-time reducible to 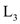 (i.e.
(i.e. ). In other
words, for all
). In other
words, for all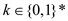 ,
,  .
.
• Assume that,  ,
,
o Then, from equation (1), 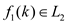 .
.
o Since, 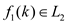 , from
equation(2),
, from
equation(2), 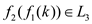 . That is
. That is
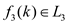
Thus, if  , then
, then 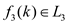 ……
(3)
……
(3)
• Let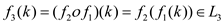 .
.
o Then according to equation (2), 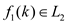
o Since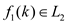 , according
to equation (1),
, according
to equation (1), 
Thus, if  ,
then
,
then  ……
(4)
……
(4)
From equations (3) & (4),  that is,
that is,
 if
and only if
if
and only if 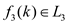 .
.
Hence, there exist a polynomial-time reduction from
 to
to 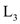 or
or  ,
if
,
if  and
and  .
.
By the definition reducibility, if 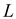 and
and
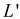 are two
languages and there is a polynomial-time computable function
are two
languages and there is a polynomial-time computable function
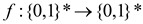 such that for all
such that for all 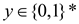 ,
, 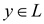 if and only
if
if and only
if 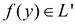 , then the
language
, then the
language 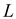 is said to
be polynomial-time reducible to
is said to
be polynomial-time reducible to 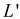 .That
is,
.That
is, 
Now, it is required to prove that  if and only
if
if and only
if  .
.
1)
Assume that  .
.
Then by the definition, for all 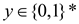
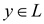 if and only if
if and only if 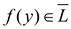
Also, 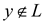 if and only
if
if and only
if 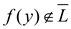
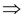
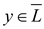 if
and only if
if
and only if 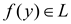 [Since,
[Since,
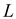 and
and 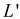 are
complement
are
complement
each other and 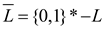 ]
]
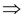

Therefore if  ,
then
,
then  ------(1)
------(1)
2) Proving converse:
Assume that  .
.
Then by the definition, for all 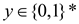
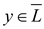 if and only if
if and only if 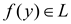
Also, 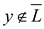 if and only
if
if and only
if 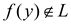
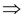
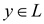 if
and only if
if
and only if 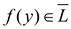 [Since,
[Since,
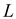 and
and 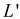 are
complement
are
complement
each other and 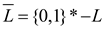 ]
]
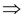

Therefore if,  then
then
 ------(2)
------(2)
From (1) and (2), it is proved that  if
and only if
if
and only if 
Consider the following alternative proof of Lemma 34.5. The Lemma 34.5 shows that CIRCUIT-SAT belongs to NP.
Here, it is given that or an encoding of a CIRCUIT-SAT problem C and a certificate that denotes an assignment of the Boolean values to every wires in the C.
Consider the following algorithm which is constructed to proof the above statement:
Algorithm:
1. Check the every gates and after that the output wires of C.
2. for every gate check the following
3. if
4. the computed value and the output value of the wires given in the
certificate is matched and the output of the overall circuit is 1
5. then
6. return 1
7. else
8. return 0
Running time complexity of the above algorithm:
• As it can be easily seen from the above algorithm that checking performed for every gate and for all gates the computed and the output values are matched.
• Therefore, the total polynomial time will be taken to perform this computation.
• Hence, it is proved that, CIRCUIT-SAT belongs to NP.
For an easier proof, the alternative certificate used is given as, “A true assignment to the inputs”.
In this user have assumed that the working storage for above algorithm holds a contiguous region of polynomial size. Below, it is show that how are user exploiting this assumption in the above lemma.
a. At the top most priority user state it to be true that the
number of bits to notify each configuration  is
polynomial in terms of n. Now, consider the program for
algorithm A has constant size,
is
polynomial in terms of n. Now, consider the program for
algorithm A has constant size,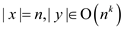 as A
runs in
as A
runs in  steps; the
total heap of work storage too will also be polynomial on
steps; the
total heap of work storage too will also be polynomial on .
.
b. The combinatorial circuit  using the
computer’s hardware has a size polynomial configuration in the
length, which is also
using the
computer’s hardware has a size polynomial configuration in the
length, which is also  and is
therefore an n polynomial term.
and is
therefore an n polynomial term.
c. Every step of algorithm that makes p takes polynomial time.
d. The circuit P contains 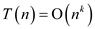 number of
configuration and that too of
number of
configuration and that too of 
Without assuming the above assumption the CIRCUIT SATISFIABILITY PROBLEM cannot be shown NP HARD.
• The term “without loss of generality” means that a proof and assumption can be used in the same related problems and cases.
• Here, it has been observed that one assumption of storage size has been taken to show it for 4 cases.
Hence it is following the without loss of generality principle and furthermore it can also be used to solve other NP HARD problems.
According to the provided information, a language L is
complete for a language class C with respect to polynomial
time reduction if 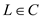 and
and
 for
all
for
all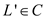 .
.
Objective is to show that 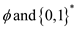 are the
only ones which are themselves present in P but are not
complete with respect to polynomial time reductions.
are the
only ones which are themselves present in P but are not
complete with respect to polynomial time reductions.
To prove that a language L in P is complete, it should be in P and every problem in P can be reduced to the problem at hand in polynomial time. This is done by the following method:
• Reduction from first problem to second problem requires mapping the “yes” instances of the first problem to the “yes” instances of the second problem.
• Then mapping the “no” instances of the first problem to the “no” instances of the second problem.
The two languages that are given are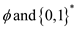 .
.
• It is already given that the languages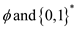 are in
P.
are in
P.
• The empty string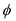 doesn’t
have any “yes” instances because it doesn’t accept any language at
all. So, every input is rejected by this language.
doesn’t
have any “yes” instances because it doesn’t accept any language at
all. So, every input is rejected by this language.
• The language 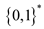 doesn’t
have any “no” instances because it accepts every language that is
composed of any combinations of two symbols – 0 and 1 including
empty combination.
doesn’t
have any “no” instances because it accepts every language that is
composed of any combinations of two symbols – 0 and 1 including
empty combination.
Since,  doesn’t
have any “yes” instances and
doesn’t
have any “yes” instances and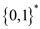 doesn’t
have any “no” instances, therefore, it is not possible to define a
reduction from any other problem in P to these problems
because all other problems have both “yes” as well as “no”
instances.
doesn’t
have any “no” instances, therefore, it is not possible to define a
reduction from any other problem in P to these problems
because all other problems have both “yes” as well as “no”
instances.
A language 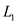 reduces to
language
reduces to
language  if and only
if there is a function
if and only
if there is a function  such that
for every string in the first language
such that
for every string in the first language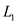 , the
function can map to second language
, the
function can map to second language and for
every string not in the first language
and for
every string not in the first language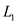 , the
function shouldn’t map it to any string of the second
language
, the
function shouldn’t map it to any string of the second
language . This
mapping should be done in polynomial time.
. This
mapping should be done in polynomial time.
Assume the languages 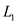 and
and
 are
in P. So, it is obvious that they can be decided in
polynomial time.
are
in P. So, it is obvious that they can be decided in
polynomial time.
The two edge cases of 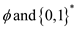 have
already been handled previously so, it has not be handled here.
have
already been handled previously so, it has not be handled here.
Let  and
and
 .
.
Now the mapping function is defined as follows:
If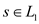 , then
, then
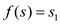 and if
and if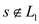 ,
then
,
then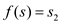 .
.
According to this, 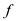 does
represent a reduction from language
does
represent a reduction from language 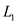 to the
language
to the
language .
.
Since both languages belong to the class of P problems,
so language 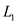 can be
solved in polynomial time and thus, the reduction function
can be
solved in polynomial time and thus, the reduction function
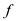 can
also be computed in polynomial time.
can
also be computed in polynomial time.
Thus, the languages 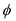 and
and 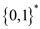 in P
except are not complete for P in polynomial time
reductions.
in P
except are not complete for P in polynomial time
reductions.
According to the exercise 34.3-6 of the textbook, a language
L is complete for a language class C with respect to
polynomial time reduction if 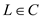 and
and
 for
all
for
all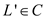 .
.
A language L is Complete for NP with respect to polynomial time reduction.
From the definition of NP-complete; if 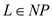 and
and
 for all
for all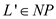 .
.
Suppose L is Complete for NP, then

If NP is closed under complement, then NP=co-NP.
So, 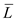 Will be Co-
NP and
Will be Co-
NP and 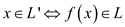 .
.
According to exercise 34.3-6, polynomial time reduction function ‘f’ is as follows:
 for all
for all 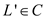
Then 
From the above equation (2)
 for all
for all 
From equation (3) it is proved that 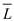 is complete
for Co-NP.
is complete
for Co-NP.
Therefore, L is complete for NP if and
only if 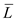 is
complete for Co-NP.
is
complete for Co-NP.