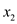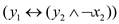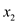Consider a circuit of size  .
.
Describe a circuit with the variables 
 where
where
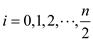 as
follows:
as
follows:

Since the total number of variables  and
and
 is
is
 ,
the size of the circuit described in (1) will be
,
the size of the circuit described in (1) will be  .
.
Refer chapter 34, section 34.4 of textbook for the theorem 34.9.
To show that CIRCUIT–SAT SAT, the
theorem reduces any instance of circuit satisfiability to an
instance of formula satisfiable in polynomial time.
SAT, the
theorem reduces any instance of circuit satisfiability to an
instance of formula satisfiable in polynomial time.
Consider, if the theorem uses non-polynomial time straightforward reduction.
If there are  variables,
then
variables,
then  assignments
are possible.
assignments
are possible.
The problem described in (1) has  variables.
So, the total number of possible combinations will be
variables.
So, the total number of possible combinations will be  .
.
Hence, the size of the Boolean formula that can be constructed
using  variables
is
variables
is  .
.
By using induction it can be proved that the formula describing
the variable  and
and
 forming a circuit of size
forming a circuit of size  has size at
least
has size at
least  .
.
Since the theorem uses non-polynomial time straightforward
reduction, the size of the formula can’t be reduced and the size
remains  .
.
Therefore, for a circuit of size  , the size of the formula is exponential in
, the size of the formula is exponential in
 .
.
Definition of 3 CNF-SAT: - It is known as the 3-Conjuctive Normal Form Satisfiability.
A literal in a Boolean formula is the occurrence of a variable or its negation. A Boolean formula is in CNF if it is expressed as a conjunction (AND ) of clauses each of which is the disjunction (OR) of one or more literals. 3 CNF means that each clause has exactly 3 literals.
For example: 
As per the Theorem 34.10
• 3-CNF-SAT NP [ Proof
same as SAT]
NP [ Proof
same as SAT]
• 3-CNF-SAT  NP-Hard:
SAT
NP-Hard:
SAT 3-CNF-SAT.
3-CNF-SAT.
Break the reduction steps into 3 steps as follows:
Step 1:
• Construct a “binary parse tree” for the input formula
 .
The tree corresponds to the formula
.
The tree corresponds to the formula  . The tree
corresponds to the formula:
. The tree
corresponds to the formula:
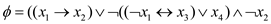
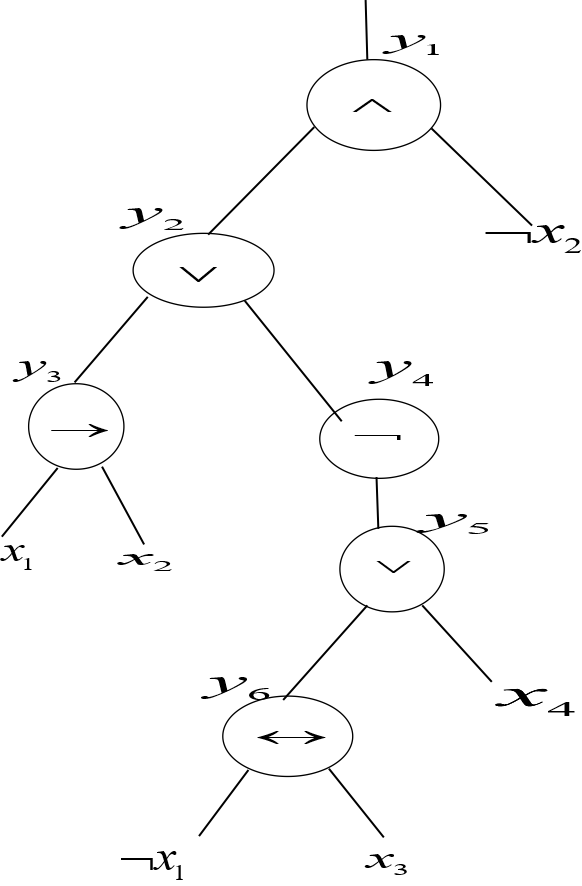
• If the formula contains the AND or OR of several literals, then it is guaranteed that that the internal nodes has just one/ two children by the parenthesis and associativity.
• The binary tree can be interpreted as a circuit for the
computation of  . In order
to obtain a 3-CNF expression, introduce a variable
. In order
to obtain a 3-CNF expression, introduce a variable  corresponding to the output of each internal node.
corresponding to the output of each internal node.
• Rewrite  as AND of
the root variable and a conjuction of clauses corresponding to
as AND of
the root variable and a conjuction of clauses corresponding to
 becomes:-
becomes:-

 is a conjuction of clauses
is a conjuction of clauses  each with
atmost three literals .
each with
atmost three literals .
Change  such that
each clause has exactly 3 literals connected with OR’s
such that
each clause has exactly 3 literals connected with OR’s
Step 2:
• Change each clause  into CNF.
Construct the truth table for each
into CNF.
Construct the truth table for each  . Each row
of the truth table consists of possible assignment of variables of
clause, together with the value of the clause under that
assignment. The truth table is as follows:
. Each row
of the truth table consists of possible assignment of variables of
clause, together with the value of the clause under that
assignment. The truth table is as follows:
|
|
|
|
|
|
1 |
1 |
1 |
0 |
|
1 |
1 |
0 |
1 |
|
1 |
0 |
1 |
0 |
|
1 |
0 |
0 |
0 |
|
0 |
1 |
1 |
1 |
|
0 |
1 |
0 |
0 |
|
0 |
0 |
1 |
1 |
|
0 |
0 |
0 |
1 |
• Using the table entries that evaluate to zero, build a formula
in DNF equivalent to  .
.
The DNF formula equivalent to  is:
is:

• Use Demorgan’s law to get the CNF formula:
In the above example, convert the clause  into CNF
and the
into CNF
and the
CNF formula is as follows:
 which is
which is
equal to the original clause  .
.
Convert all other formulae  into CNF.
Each clause has no more than 3 literals corresponding to two input
and one output associated with the nodes of binary parse tree for
into CNF.
Each clause has no more than 3 literals corresponding to two input
and one output associated with the nodes of binary parse tree for
 .
.
Step 3:
• Modify  so that all
its clauses have exactly 3 distinct literals.
so that all
its clauses have exactly 3 distinct literals.
Perform this transformation in several steps.
Modify each clause  of
of
 after
introducing new variables p and q.
after
introducing new variables p and q.
o If  has 3
distinct literals: do nothing.
has 3
distinct literals: do nothing.
o If  has 2
distinct literals:
has 2
distinct literals:  . Replace
. Replace
 by
by
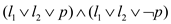 which is equivalent to
which is equivalent to 
o If  has 1
literal:
has 1
literal:  . Replace
. Replace
 by
by
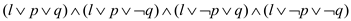 .
.
Now, show that the 3-CNF formula of  is
satisfiable, if
is
satisfiable, if  is
satisfiable .
is
satisfiable .
Examine the 3 reduction steps as follows:
Step 1: The binary tree circuit is another representation
of the formula. It will be satisfiable if the formula  is
satisfiable. Apply the induction proof on the number of
clauses.
is
satisfiable. Apply the induction proof on the number of
clauses.
Step 2: Demorgan’s law is used to produce a formula which
is algebraically equivalent to the original one, that is,  .
.
Step 3: The new formula is effectively equivalent to the one produced in the Step 2, since a formula algebraically equivalent to that produced in Step 2 is produced by the assignment of the new variables p and q.
The 3-SAT is a satisfiability problem where the Boolean formula has only 3 literals or variables ORed to each other in each clause that are ANDed. The output of each of the clauses should give the output of the whole problem as 1.
It means that we should choose the values of the literals or variables used in the formula so that the output is 1 then only the formula is satisfiable.
The 3-CNF SAT is a SAT problem with 3 such literals as variables, and 2 CNF SAT is a SAT problem with two literals as variables.
For the proof of 3-CNF SAT to be NPC, consider the following
3-CNF SAT given in equation form by using 3 literals  as:
as:

Now for each clause we need to draw a parse tree and find the corresponding truth table as for example the first clause is been described as follows.
We draw a parse tree and treat the connectives as nodes and the leaf nodes as the literals:
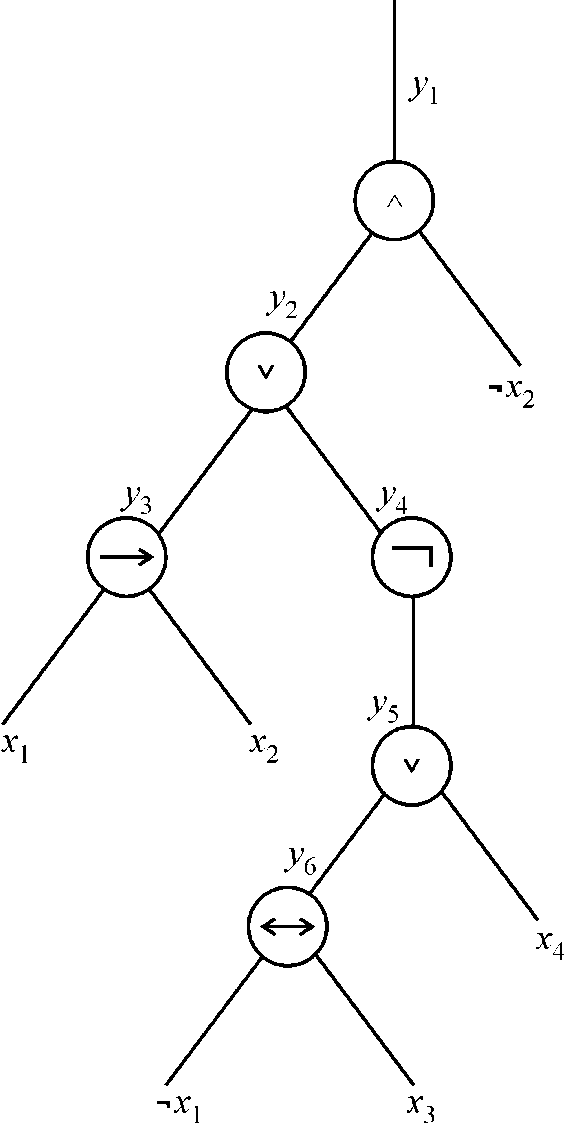
Corresponding to the above parse tree the result 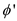 of the
expression
of the
expression  is derived
and represented as:
is derived
and represented as:

The truth thus derived for the 1st clause that is the
truth table for  is as:
is as:
|
|
|
|
|
|
0 |
0 |
0 |
1 |
|
0 |
0 |
1 |
1 |
|
0 |
1 |
0 |
0 |
|
0 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
|
1 |
0 |
1 |
0 |
|
1 |
1 |
0 |
1 |
|
1 |
1 |
1 |
0 |
We know that the length of the parse tree is the total height
traversed, that is, of the form  where
n is the number of leaves. Now this is of the form
where
n is the number of leaves. Now this is of the form 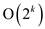 which is a
non- polynomial form.
which is a
non- polynomial form.
So to find out the total value of the formula we need to perform the same task for every clause. This results in a non-polynomial degree.
The 3 CNF form is:
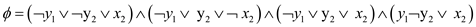
Hence by taking the values of the truth table the number of values increases creating a non polynomial reduction. So this strategy does not yield a polynomial time reduction.
Determining Whether a Boolean Formula is a Tautology is Complete for co-NP
Boolean Formula: It is the logic or a combination of the
variables as inputs and the different binary or unary operators. It
is a form of the algebraic expressions that can have only two
possible forms or results as either true or false. It is a
combination of the operators such as OR ,
AND
,
AND ,
NOT
,
NOT and many
more.
and many
more.
For example: Consider the Boolean formula given below:
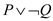 is a valid Boolean formula and P is not an example of a
valid Boolean formula.
is a valid Boolean formula and P is not an example of a
valid Boolean formula.
The result obtained is either true or false, 0 or 1 depends mainly on the type of operators and the input variables of the Boolean formula or expression.
Tautology: It denotes a compound preposition or a formula which uses the combination of different input variables to generate a true value for all the possible combinations. It is one of the simple examples of the NP- complete problem. Thus, it is a way or form of achieving a true or 1 value in a predicate calculus.
For example: Consider the Boolean formula or expression
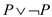 which is a tautology as shown in the truth table given below:
which is a tautology as shown in the truth table given below:
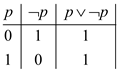
As the value of the Boolean formula 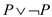 is coming
out to be 1, so it can be stated that this is a tautology. In case
of a Boolean formula, it can be considered as a tautology or
unsatisfiability depending on the values provided to the input
variables. The formula will be a tautology in case when the formula
evaluates to 1 or true.
is coming
out to be 1, so it can be stated that this is a tautology. In case
of a Boolean formula, it can be considered as a tautology or
unsatisfiability depending on the values provided to the input
variables. The formula will be a tautology in case when the formula
evaluates to 1 or true.
In other words, it can be said that whenever the variables are assigned or provided with the values in the form of true or false this operation always yields a result or an outcome as a True statement. This is similar to the problem of determining or finding that whether at least one assignment of such type is present or not. Thus, in order to verify whether a Boolean formula is a tautology or not, certification in the form of Boolean variables can be used.
Hence, this proves that 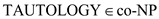 .
.
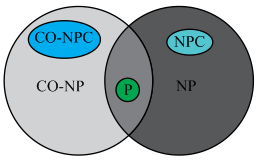
Co-NP: Co-NP stands for NP problems that are NP complete. Co-NP complete represents the class of problems or languages whose complement belongs to NP.
Consider 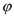 be a Boolean
formula constructed from the following terms stated below:a.
The Boolean input variables
be a Boolean
formula constructed from the following terms stated below:a.
The Boolean input variables  ;
;
b. OR’s 
c. AND’s 
d. Negations 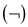
e. At most, one pair of Parentheses present in the
Boolean formula per Boolean connective which are OR’s , AND’s
, AND’s
 and
Negations
and
Negations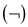 .
The
.
The 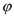 Boolean formula
will be a tautology if and only if it outputs to 1 for every
assignment of 1and 0 for all the input variables.
Boolean formula
will be a tautology if and only if it outputs to 1 for every
assignment of 1and 0 for all the input variables.
As it is known that, co-NP belongs to the set of languages,
which follows that L-complement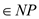 ; further
if, it can be shown that TAUTOLOGY-complement
; further
if, it can be shown that TAUTOLOGY-complement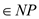 , then that
will prove the statement or fact that
, then that
will prove the statement or fact that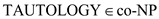 . Set not
TAUTOLOGY=TAUTOLOGY-complement.
. Set not
TAUTOLOGY=TAUTOLOGY-complement.
Now, it is known that a language L belongs to NP, only if there exists two-input polynomial-time algorithm A and constant c so that:
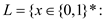 There exists a certificate
There exists a certificate 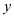 with
with 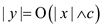 such
that
such
that 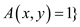
Now, try to find for each formula x, to find out
if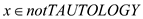 ,
try all possible combinations of 0 and 1 assignments to input
variables unless any one assignment finds out that comes to be
FALSE.
,
try all possible combinations of 0 and 1 assignments to input
variables unless any one assignment finds out that comes to be
FALSE.
Hence, to know whether a given formula belongs to not
TAUTOLOGY, it is required to use a certificate 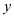 of
length
of
length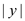 of at least
of at least
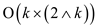 for
algorithm A to be verified for all the combination possible
made from 0 and 1 for all k input variables of x.
for
algorithm A to be verified for all the combination possible
made from 0 and 1 for all k input variables of x.
Therefore, no certificate y with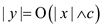 containing
c constants can be done for an algorithm
containing
c constants can be done for an algorithm 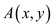 to check it
up for whether x is accepted or not.
to check it
up for whether x is accepted or not.
Hence, 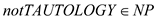 and
thus, it is proved that
and
thus, it is proved that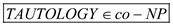 .
.
Disjunctive Normal Form (DNF):
A Boolean formula that is composed of OR of clause of ANDs is known as DNF.
The Boolean formula of the form DNF is satisfiable if any of its clause can be evaluated as 1.
For some variable 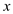 such that
the clause contains
such that
the clause contains 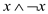 irrespective of the Boolean value
irrespective of the Boolean value 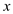 will be
evaluated to 0. Otherwise, for some assignment of values 0 and 1
the clause will be evaluated to 1.
will be
evaluated to 0. Otherwise, for some assignment of values 0 and 1
the clause will be evaluated to 1.
The following is the algorithm to determine the satisfiability of Boolean formula in DNF:
Algorithm DNF–SAT 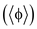 :
:
1 for each clause  of
of
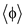
2 for variable 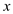 such that
such that
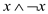
3 if 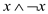 exists in
the clause
exists in
the clause  of
of
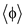
4 retrun false
5 else
6 retrun true
7 end for
8 end for
Running Time Analysis:
• Consider 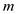 be the
total number of clauses and each clause has at most
be the
total number of clauses and each clause has at most  (literals)
variables in
(literals)
variables in 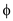 .
.
• The loop in the line 1 and its block in the lines 2–8 runs at
most 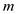 times.
times.
• The loop in the line 3 and its block in the lines 2–7 runs at
most  times.
times.
• The block in the lines 3–6 takes at most  time as the
existence of
time as the
existence of 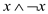 in the
clause
in the
clause  will take
will take
 steps.
steps.
• So the running time of the algorithm is 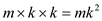 .
.
• Hence the time complexity of the algorithm DNF–SAT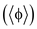 is
is  .
.
Therefore, the problem of determining whether the satisfiability of Boolean formulas in DNF form is polynomial-time solvable.
The language for formula satisfiability problem is SAT=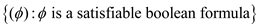 .
.
Let A denote the polynomial time algorithm which returns 1 if the input x is a satisfiable formula and 0 otherwise.
In addition, assume  has at most
n variables denoted as
has at most
n variables denoted as 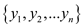 .
.
The following procedure can be used to find satisfying assignments in polynomial time:
• Apply the polynomial time algorithm A on the Boolean formula
 to
determine whether
to
determine whether  is
satisfiable or not. If it is not satisfiable return 0 else
continue.
is
satisfiable or not. If it is not satisfiable return 0 else
continue.
• Initialize a variable, i =1.
• Let the variable  then the
condition that
then the
condition that  is a Boolean
formula with n-i variables is satisfied.
is a Boolean
formula with n-i variables is satisfied.
• Apply the algorithm A to check the satisfiability that is,
there must be an assignment of  that
satisfies
that
satisfies  .
.
• Replace the variable  in Boolean
formula
in Boolean
formula  by the
recorded value from the previous step and then increment the
variable i by 1, repeat the previous step until i = n.
by the
recorded value from the previous step and then increment the
variable i by 1, repeat the previous step until i = n.
• Return the recorded assignments for all the variables
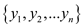 .
.
• Since, the algorithm A runs in polynomial time, so the above procedure runs in polynomial time.
2-CNF-SAT- PROBLEMS
A Satisifiability problem represents the class of problems in which the formula is passed as an input having the conjunction of clauses. A Boolean formula in which each clause is a disjunction of literals containing the variables having the values either as true or false is known as the CNF (Conjunctive Normal Form). In case of Boolean formulas, CNF is mainly used for describing the clause set representation.
For Example: The Boolean formula given below is in Conjunctive Normal Form (CNF)
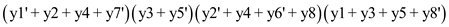
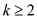 .
.The word 2-SAT refers to 2-satisfiability which refers to that class of problem having a group of two-valued variables (that is Boolean or binary) which satisfies the constraints on the variables. The instances of 2-satisfiability problem can be expressed as 2-CNF (Conjunctive Normal Form) in which the numeric value 2 denotes the number of terms per clause.
If a collection of sub-expression called clauses, that are
combined or arranged using AND contains at most two literals in
case of a Boolean formula then a variant of SAT problem is known as
the 2-CNF-SAT PROBLEM, which is a well-known
restriction of the CNF-SAT. This problem can be easily explained
using the Boolean expression having some restriction in the form of
a conjunction of disjunction which basically denotes AND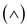 of
OR’S
of
OR’S .
.
Consider the two arguments for each disjunction operation (or operation) which may be a variable or its negation. The word term and clauses will be used frequently in this problem which is defined as,
Terms: It is the appearance of variables and their negation.
Clauses: It is the pairs of terms in the disjunction.Consider the input having a Boolean formula 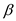 in the
conjunctive normal form in which each clause contains two literals
(one is variables and the other is its negation) and the size of
the formula is defined by the number of clauses. The clause
in
in the
conjunctive normal form in which each clause contains two literals
(one is variables and the other is its negation) and the size of
the formula is defined by the number of clauses. The clause
in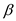 has the variables m and n and the literal is set in
such a way that m appears to be 0. The value of n
must be fixed in order to have the clause to be true.
has the variables m and n and the literal is set in
such a way that m appears to be 0. The value of n
must be fixed in order to have the clause to be true.
After fixing the value of n it may be possible that a case arises when any other clause containing n requires the other value of literal to be fixed. And in this way there will be the requirement of the exchange operation.
Now, if during the process a clause 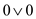 is
encountered, it signifies that the decision that was taken or
considered for the variable m does not proceed towards the
Satisifiability.
is
encountered, it signifies that the decision that was taken or
considered for the variable m does not proceed towards the
Satisifiability.
So it is required to look or opt for an opposite choice for
variable m. And if the clause 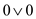 has been
found again then it is sure that the Boolean formula
has been
found again then it is sure that the Boolean formula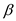 is not
satisfiable. Thus, whole process will be repeated till all the
variables from the Boolean formula
is not
satisfiable. Thus, whole process will be repeated till all the
variables from the Boolean formula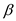 are removed
or eliminated.
are removed
or eliminated.
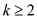 represents
the time complexity of the algorithm and the formula is traversed
twice for settingthe value of the variable.
represents
the time complexity of the algorithm and the formula is traversed
twice for settingthe value of the variable.Algorithm:
for each variable v
if a path from 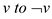 and
from
and
from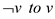
return “rejection”
else
return “accept”
As per the above algorithm the Boolean formula will be
satisfiable only in a case that there should not be any pair of
complementary literals present in the same strongly connected
graph. In other words, it can be said that an interpretation will
exist for the formula if and only a variable and its negation are
not a part of a strongly connected component. The algorithm first
determines that for each variable v if there is a path from
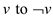 and from
and from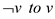 .The
rejection is done if we have a success for any of these tests,
otherwise the acceptance is done.
.The
rejection is done if we have a success for any of these tests,
otherwise the acceptance is done.
Above explanation implies that 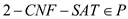 is
solvable in polynomial time and thus, it is polynomial time
decidable.
is
solvable in polynomial time and thus, it is polynomial time
decidable.