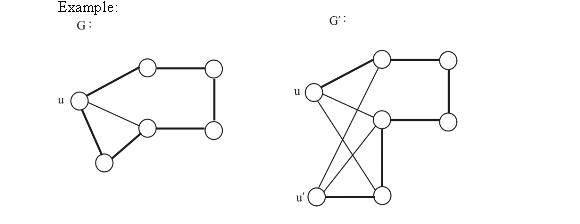
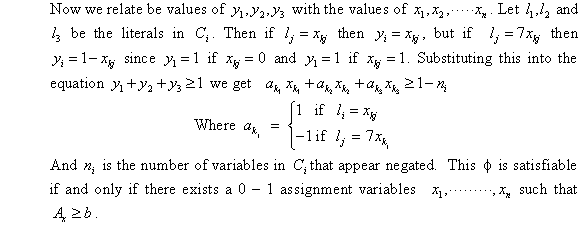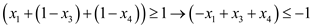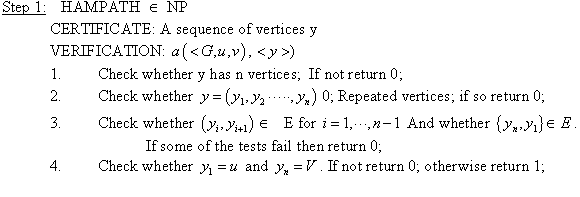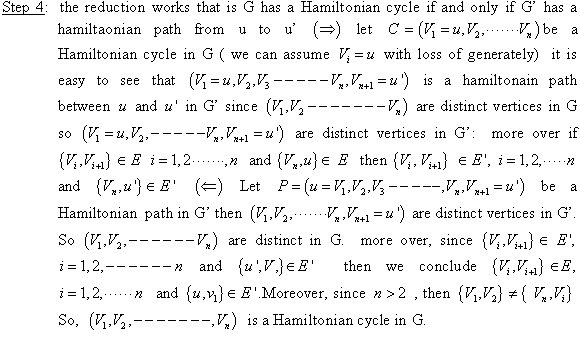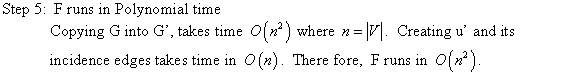In the graphs shown above, it can be seen that sub graph
 of
graph S is isomorphic because it has the existence of the
graph G and the sub graph
of
graph S is isomorphic because it has the existence of the
graph G and the sub graph  is not.
is not.
• Sub-graph Isomorphism is a NP-Complete problem.
• For this decision problem to be classified as NP-Complete problem, it must also satisfy both NP and NP-Hard category.
• To prove this problem as NP-Complete problem, the following two things have to be proved:
i. The decision problem should be in NP category (NP category)
ii. Every problem in NP must be reducible to this decision problem in polynomial time (NP-hard category)
Proof that Sub-graph Isomorphism is in NP category:
NP is a set of decision problems such that the solutions of these problems can be verified in polynomial time.
Given a description of graph sub-graph S1 and the mapping between the vertices of the sub-graph S1 and the vertices of the graph G, it takes polynomial time to verify S1 is indeed isomorphic to the graph G.
The mapping describes which vertices of S1 correspond
to which vertices of G. This mapping is represented by the
function .
.
1. For each edge (u, v) of graph S, if it belongs to
S1, then edge 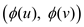 also belongs
to graph G
also belongs
to graph G
2. Repeat this for each edge of graph S.
This requires traversing through all the edges of graph S, and then for each of these edges, matching is done with the set of vertices of S1 and G.
So, time complexity should be at most 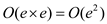
This is same as  for dense
graphs and
for dense
graphs and  for sparse
graphs.
for sparse
graphs.
Thus, it can be seen that sub-graph isomorphism is verified in polynomial time.
Therefore,  .
.
Proof that every problem in NP is reducible to Sub-graph Isomorphism decision problem (NP-Hard category):
All NP-complete problems belong to the NP category also. Clique problem is a known NP-complete problem. By definition, all NP problems are reducible to Clique problem. Thus, if Clique problem is reducible to the sub graph isomorphism problem, then the every NP category problem should also be reducible to the sub-graph isomorphism problem.
Clique Problem: It is a NP-complete decision problem in which the input is a single graph S and a number k, such that the question is to find out whether S contains a complete sub-graph with k vertices.
Reduction: Clique problem can be reduced to sub-graph isomorphism problem by the following steps:
1. Create G as a complete graph of k vertices.
2. CLIQUE (Graph, number) is given an input of S and k.
If this gives the answer as “yes”, then the graph S must be containing a sub-graph S1 such that the S1 is a k-clique. Since, G is already a k-clique. Therefore, this sub-graph is isomorphic.
The reduction requires having an instance of the CLIQUE which
accepts a graph and a number. The graph S is copied to it. Copying
a graph takes 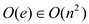 time
complexity. There needs to be graph G specified which must be a
complete graph. Writing a complete graph again takes a time
complexity of
time
complexity. There needs to be graph G specified which must be a
complete graph. Writing a complete graph again takes a time
complexity of . Thus, the
whole reduction is done in polynomial time.
. Thus, the
whole reduction is done in polynomial time.
Since, clique problem is reducible to the sub graph isomorphism problem, so every NP category problem must also be reducible to the sub-graph isomorphism problem.
Since, it is proved that sub-graph isomorphism problem belongs to NP category and that all the NP category problems are reducible to sub-graph isomorphism problem, therefore, it is true that sub-graph isomorphism problem is a decision problem that is NP-complete.
The 0-1 integer programming problem will be proved as
NP-complete by using the fact that 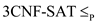 0-1
integer-programming problem.
0-1
integer-programming problem.
Now, consider a CNF formula 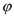 that
contains
that
contains  variables
and
variables
and 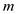 clauses.
Now, construction the corresponding matrices
clauses.
Now, construction the corresponding matrices 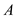 and
and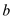 are as
follows:
are as
follows:
• First transform every clause into the inequality and,
• An expression  and
and
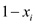 are
used to denote every literals depends whether it is a variable or
its negation which exists in the clause.
are
used to denote every literals depends whether it is a variable or
its negation which exists in the clause.
Now, consider the following examples:
Here, the CNF formula 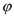 is given
as
is given
as .
Then, the following will be exists:
.
Then, the following will be exists:
|
|
|
|
|
|
Then from the above given CNF formula, matrix corresponds to
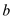 and
and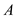 are given
as:
are given
as:
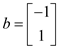 and
and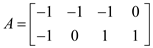 .
.
Consider the following reduction algorithm:
FREDUCTION (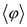 )
)
1. First performed checking whether the format of 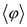 is in 3-CNF
or not.
is in 3-CNF
or not.
2. If the format is not in 3-CNF then return 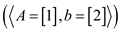
//for loop is used to iterate through 1 to m, where 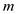 is the
clauses.
is the
clauses.
3. for k=1 to m
//Assign value zero to the variable NUM
4. NUM 0;
0;
5. for i=1 to m do
6. 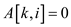 ;
;
7. for every literals do
8. if  then
then
9. 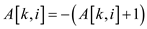 ;
;
10. else if  then
then
11. 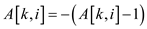 ;
;
12. NUM++;
13. end if
14. end for
15. 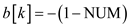 ;
;
16. end for
17. retrun 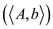
Use the algorithm in the above step to find the format of
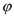 .
.
Now, consider if the format of 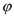 is not in
3-CNF then
is not in
3-CNF then 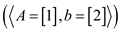 and the
system has no solution for
and the
system has no solution for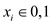 .
.
• In this case, if there exists a truth assignment to  in such way
that every clause is satisfiable then
in such way
that every clause is satisfiable then 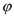 is said to
be satisfiable.
is said to
be satisfiable.
• Then, it is true if there exists the values 0, 1 assigned to
variables  in such way
that
in such way
that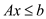 .
.
Hence, form the above explanation it is proved that “integer programming problem is NP-complete”.
The subset-sum problem deals with finding out whether there exists a subset from the elements provided such that their sum is equal to a specific value.
Assume 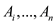 is the
sequence of positive integers.
is the
sequence of positive integers.
n is the number of elements in the set A.
Let the required sum of subsets be denoted by t such that t > 0.
Define 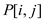 for all
for all
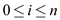 and
and 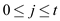 to
calculate whether there is a subset with required sum or not.
to
calculate whether there is a subset with required sum or not.
The value of 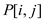 will be
true only if there is subset of
will be
true only if there is subset of 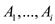 otherwise
false.
otherwise
false.
So,
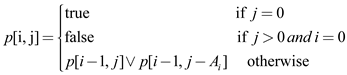 …… (1)
…… (1)
This being a Dynamic Programming algorithm, solving for smaller problems is done first and it is then used to solve the bigger problems.
From equation (1), the following is observed:
• 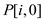 will be
true for all value of i
will be
true for all value of i
• 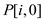 will be
false for all
will be
false for all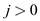 .
.
• For other values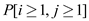 , it is
true only if there is a subset of A1,
A2, A3…. Ai-1
summing to j or j-Ai.
, it is
true only if there is a subset of A1,
A2, A3…. Ai-1
summing to j or j-Ai.
Thus, the term 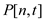 gives the
final answer to the problem.
gives the
final answer to the problem.
From the above algorithm, it is clear that the running time depends on two loops:
• The value 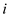 increases
from 0 to n.
increases
from 0 to n.
• The value j increases from 0 to t.
The second loop is contained within the first loop.
In such a scenario, the final time complexity becomes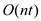 where
n is the number of elements and t is the maximum
element.
where
n is the number of elements and t is the maximum
element.
Time complexity if the target value t is in unary notation:
Let the number of bits required to represent the maximum number t is b.
In case of unary notation, the number of bits required to represent the numbers is at most equal to the greatest number which is t. This is because t is represented by t number of 1s.
So, number of bits required to represent the numbers is at most
t. So, b is upper bounded by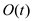 .
.
The final complexity becomes .
.
Thus, if the target value t is expressed in unary, then the subset-sum problem is solved in polynomial time.
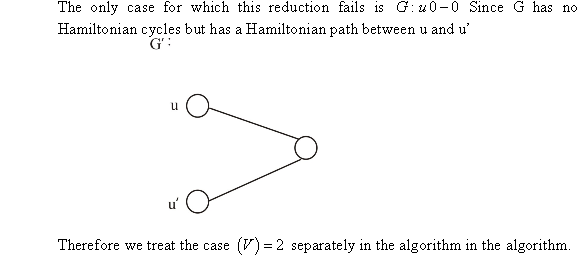
Consider the following decision version of the longest simple cycle problem:
• LONGESTSIMPLECYCLE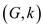 : for a
given integer
: for a
given integer  and an
undirected graph
and an
undirected graph , does
, does
 has
a simple cycle of length minimum
has
a simple cycle of length minimum .
.
• Now, to show LONGESTSIMPLECYCLE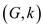 is
NP-complete, first consider the following definition of
HAMCYCLE
is
NP-complete, first consider the following definition of
HAMCYCLE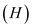 .
.
• HAMCYCLE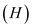 : For a
given undirected graph
: For a
given undirected graph 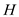 does
does
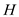 consists a
Hamiltonian cycle.
consists a
Hamiltonian cycle.
LONGESTSIMPLECYCLE 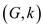
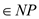 :
:
• Suppose an instance of LONGESTSIMPLECYCLE is denoted
as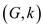 .
Now, consider the certificate y that consists a sequence of
vertices.
.
Now, consider the certificate y that consists a sequence of
vertices.
• Now, simply scanning performed through the graph  in
polynomial time to verify that y consists a cycle, length of
y is k of higher and no vertex in y appears
more than once.
in
polynomial time to verify that y consists a cycle, length of
y is k of higher and no vertex in y appears
more than once.
HAMCYCLE 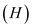
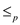 LONGESTSIMPLECYCLE
LONGESTSIMPLECYCLE 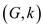 :
:
• An instance LONGESTSIMPLECYCLE is
constructed from the instance of HAMCYCLE
is
constructed from the instance of HAMCYCLE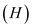 . It can be
done in polynomial constant time as the instrumentation is
trivial.
. It can be
done in polynomial constant time as the instrumentation is
trivial.
• Now, the graph 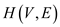 consists a
Hamiltonian cycle, if its longest simple cycle length is equal
to
consists a
Hamiltonian cycle, if its longest simple cycle length is equal
to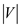 .
It is correct because, if
.
It is correct because, if 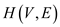 consists a
Hamiltonian cycle that cycle is a simple path, which consists a
length
consists a
Hamiltonian cycle that cycle is a simple path, which consists a
length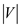 .
.
• On the other hand, the length of the longest simple in
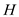 must be
strictly less than
must be
strictly less than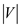 if
if 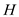 does not
consists a Hamiltonian cycle.
does not
consists a Hamiltonian cycle.
Hence, the LONGESTSIMPLECYCLE 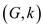 is
NP-complete can be concluded from the above proofs.
is
NP-complete can be concluded from the above proofs.