Algorithm of vertex cover problem: The vertex cover problem is the problem of finding the subset of vertices that cover all the edges of the graph.
Refer chapter 35, section 35.1 for the
APPROX-VERTEX-COVER algorithm.
algorithm.
The APPROX-VERTEX-COVER algorithm performs the following steps:
• Initializes the vertex set with an empty set.
• After that, copies edge set to a temporary variable.
• Then it selects each edge of the graph one by one and adds the vertices that cover to the vertex cover set. It updates the set by adding vertices to it.
• After that it removes the edge from the edge set.
• This process is repeated till the time the edge set is empty and all the edges in the graph are covered.
• At the end of the algorithm, it returns the vertex cover.
Example of a graph for which the algorithm always yields a suboptimal solution:
Consider a graph with two vertices and an edge between them.
The vertex cover consists of a single vertex, which is the optimal vertex cover.
The APPROX-VERTEX-COVER algorithm
returns both vertices in this case.
algorithm
returns both vertices in this case.
The following is the graph G:

The above graph with two vertices and one edge is the example
for which the algorithm APPROX-VERTEX-COVER  always yields a suboptimal solution.
always yields a suboptimal solution.
The following is the graph G is another example:
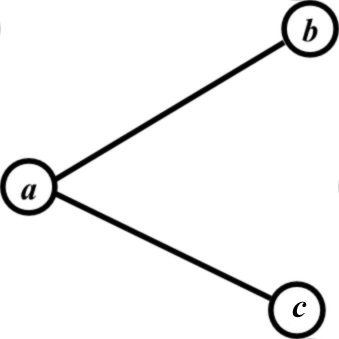
The above graph has three vertices and two edges.
The algorithm APPROX-VERTEX-COVER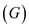 returns all
the three edges. So, the algorithm always yields a suboptimal
solution.
returns all
the three edges. So, the algorithm always yields a suboptimal
solution.
For an undirected graph, the vertex cover is defined as the collection of vertices that can cover all of the edges of the concerned graph.
Consider the graph  and the set
and the set
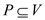 .
.
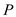 is called the vertex cover, if it covers all the edges
is called the vertex cover, if it covers all the edges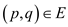 and
and
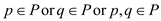 .
.
The number of vertices in the set 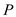 is called
the size of the vertex cover.
is called
the size of the vertex cover.
Maximal matching:
A matching M is said to be maximum matching of a
graph G, if M is not properly contained in any other
matching, that is 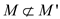 where
where
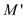 is
any other matching of graph G.
is
any other matching of graph G.
Algorithm of vertex cover problem: The vertex cover problem is the problem of finding the subset of vertices that cover all the edges of the graph.
Refer chapter 35, section 35.1 for the
APPROX-VERTEX-COVER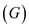 algorithm.
algorithm.
The APPROX-VERTEX-COVER algorithm performs the following steps:
• Initializes the vertex set with an empty set.
• After that copies edge set to a temporary variable.
• Then, it selects each edge of the graph one by one and adds the vertices that cover to the vertex cover set. It updates the set by adding vertices to it.
• After that it removes the edge from the edge set.
• This process is repeated till the time the edge set is empty and all the edges in the graph are covered.
• At the end of the algorithm, it returns the vertex cover.
The line 4 of the algorithm APPROX-VERTEX-COVER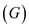 , pick an
edge.
, pick an
edge.
Once edge is selected, all the edges that are incident on any of the nodes to the edges are removed in the line 6. The rest of the edges that remain will form the maximum matching M in the graph G.
The process is repeated till the vertex cover is formed. The edges that remained after all the iterations form the maximum matching M in the graph G.
Therefore, the line 4 of the algorithm
APPROX-VERTEX-COVER 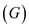 forms the maximum matching M in the
graph G .
forms the maximum matching M in the
graph G .
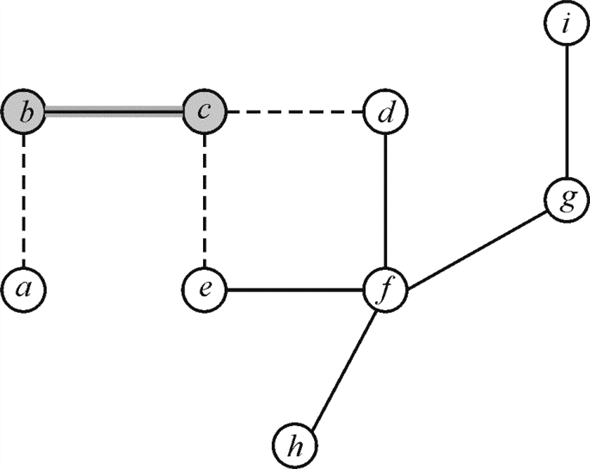
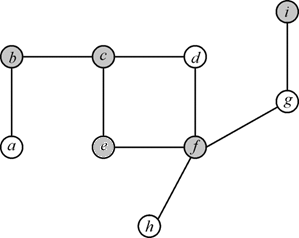
Consider the graph given below:
In the graph there are 7 vertices in the vertex set 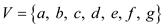 and 8 edges
named
and 8 edges
named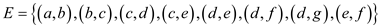 .
.
Consider the algorithm above for covering the edges. The following diagrams represent the state of the graph iteration by iteration of the algorithm.
Whenever an edge is chosen and the attached vertices are traversed; remaining of the edges connected to those vertices are removed from the sub-graph. This is done because the vertices attached to those edges have been covered already.
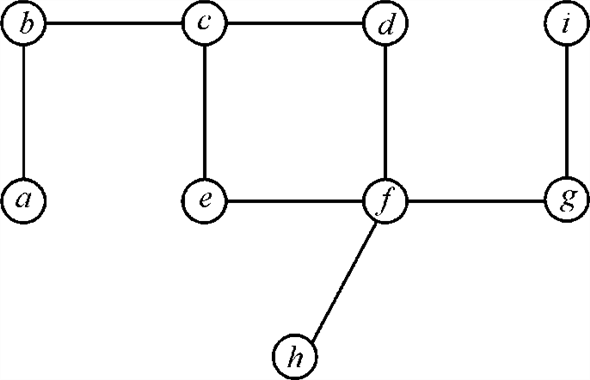
1. First the edge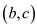 is chosen
and the vertices b and c are added to the set of
vertex cover C. That is the updated set is
is chosen
and the vertices b and c are added to the set of
vertex cover C. That is the updated set is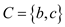 . The edges
incident on added vertices b and c that is
. The edges
incident on added vertices b and c that is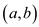
 and
and
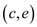 are
removed from the graph as shown by the dotted lines:
are
removed from the graph as shown by the dotted lines:
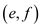 is chosen
and the vertices e and f are added to the set of
vertex cover C. That is the updated set is
is chosen
and the vertices e and f are added to the set of
vertex cover C. That is the updated set is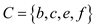 . The edges
incident on added vertices b and c are
. The edges
incident on added vertices b and c are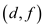
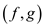 and
and
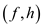 which
are removed from the graph in this step. The graph after this step
is as shown below:
which
are removed from the graph in this step. The graph after this step
is as shown below:
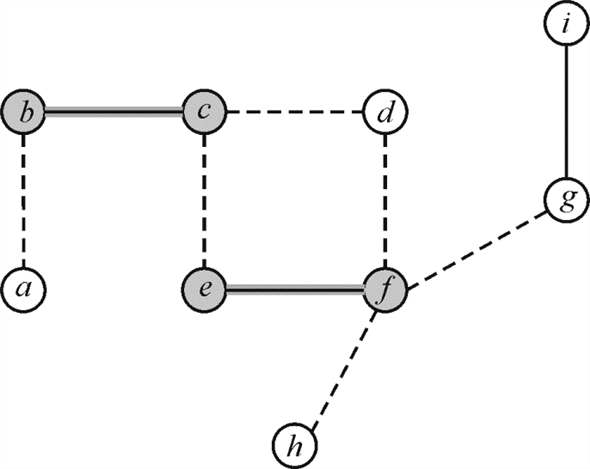
3. In the next iteration, the edge  is selected
from the remaining edge set. The updated vertex cover set
is
is selected
from the remaining edge set. The updated vertex cover set
is .
As the entire edges incident on the vertices g and i
are already removed from the graph so no edges are removed in this
step.
.
As the entire edges incident on the vertices g and i
are already removed from the graph so no edges are removed in this
step.
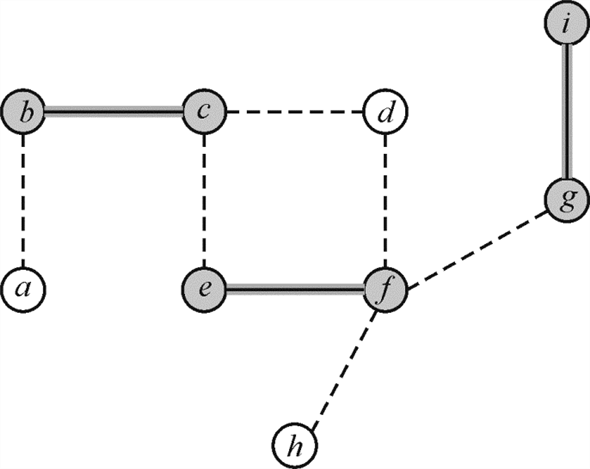
Now, the cover set C contains six vertices and the sub-optimal vertex cover contains only four vertices.
Hence, the vertex cover for the graph  is
is 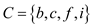 the graph
showing vertex cover is as follows:
the graph
showing vertex cover is as follows:
Explanation:
The APPROX-VERTEX-COVER algorithm chooses a random edge and then deletes the edges incident init.
This process is continued till all the vertices are covered.
Firstly edge 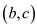 is chosen
(Figure-2), then
is chosen
(Figure-2), then 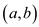
 and
and
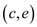 edges are removed from the graph.
edges are removed from the graph.
Next Edge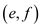 is chosen
and edge
is chosen
and edge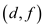
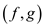 and
and
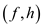 are
discarded.
are
discarded.
Lastly the edge 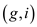 is
selected. After that no edge remains to be discarded.
is
selected. After that no edge remains to be discarded.
So, the vertex cover set is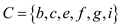 .
.
From the above steps, it can be observed that the line 4 of the
algorithm forms maximal matching. The edges picked up in line 4
are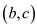 ,
,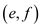 and
and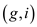 .
.
Vertex Cover Problem
The vertex cover problem is the problem in which we try to find out a set of vertices S from an undirected graph G, so that every edge of graph G has minimum one of its endpoint in S. Vertex cover problem is a NP-hard problem.
Heuristic technique refers to the techniques developed on some personal learning and self experience to find out or discover a new method. This technique if implemented tends to shorten the time period of solving a problem.Now, we have to show in our solution that whatever heuristic Professor has applied, it will not have approximation ratio of 2. The following graph will not give approximation ratio of 2 using the proposed heuristic given by Professor. The vertices of graph are:
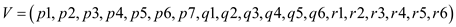
And the adjacency list representation is:
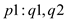
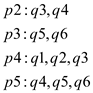
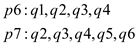
There should be an edge from 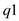 to
to
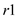 and from
and from 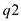 to
to
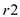 and so on.
and so on.
The heuristic proposed is an 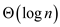 approximation algorithm. For the upper bound the algorithm is
greedy set cover algorithm, where edges are the path to be traced
and every node depicts a set comprising of edges incident to this
node, and greedy set cover have approximation time
approximation algorithm. For the upper bound the algorithm is
greedy set cover algorithm, where edges are the path to be traced
and every node depicts a set comprising of edges incident to this
node, and greedy set cover have approximation time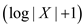 . For the
lower bound take the bipartite graph
. For the
lower bound take the bipartite graph 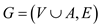 constructed
as following. Consider
constructed
as following. Consider and
and .
.
Connect all  to
to
 for each
for each . Then add
. Then add
 nodes to
nodes to  and each of
them to exactly two nodes of
and each of
them to exactly two nodes of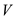 , not
connected to any other of the added nodes. Now add
, not
connected to any other of the added nodes. Now add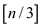 nodes and
continue adding nodes like this. At last
nodes and
continue adding nodes like this. At last 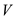 contains
contains
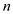 nodes and
nodes and 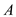 contains
contains
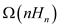 nodes.
nodes.
Now, it is clear that 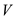 is the
optimal vertex cover, but algorithm will select
is the
optimal vertex cover, but algorithm will select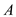 . Therefore,
we have lower bound of
. Therefore,
we have lower bound of 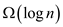 as
approximation factor. Thus it is seen that we are not getting
approximation factor of 2 anywhere. Hence, the heuristic proposed
by Professor proves to be wrong.
as
approximation factor. Thus it is seen that we are not getting
approximation factor of 2 anywhere. Hence, the heuristic proposed
by Professor proves to be wrong.
Optimal vertex-cover:
Vertex-cover of a graph G= (V, E) is a subset V' of the set of vertices V such that each edge of the graph is incident to at least one vertex of V'. The vertex-cover problem finds the optimal (minimum size) vertex-cover of a given graph.
The algorithm APPROX-VERTEX-COVER (G) finds the vertex cover of a given graph G. but it is not an optimal vertex-cover.
The following is the greedy algorithm to find an optimal vertex cover of a given tree.
OPTIMAL-VERTEX-COVER (T)
//initially store all node of tree into set
1.  = all
the nodes of tree T
= all
the nodes of tree T
2.  = all the
edges of the tree T
= all the
edges of the tree T
// initialize variable C to store the vertex cover
3. C=NIL
//Exit from the loop, if  is
empty
is
empty
4. While  !=
NIL
!=
NIL
5. Select a node v such that v has at least one leaf
//Update the vertex covers C by adding v to C
6. 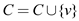
7. Update  by
removing the v and all the vertices incident to v
from
by
removing the v and all the vertices incident to v
from  .
.
//finally returns the vertex cover
8. return C
• The above OPTIMAL-VERTEX-COVER algorithm returns an optimal vertex-cover C for a given tree T. in the line 1,2, two sets are initialized. One set is the set of vertices in the tree T. another is the set of edges in the tree T
• Initially the set C contains no vertex.
• In the line 4, while loop checks whether the set of vertices is empty or not.
• If the set is not empty, then a vertex v that has at least one leaf is selected in the line 5 and the vertex v is added in the line 6.
• Now the vertex and it’s all neighboring nodes are removed from
the set  .
.
• Step 4 to 7 are repeated, until all the vertices are removed
form the set  .
.
Time complexity:
The above OPTIMAL-VERTEX-COVER selects the node v in each iteration optimally in O(n). That is, the algorithm runs linearly.
Hence the time complexity of algorithm will be
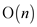 .
.
Refer theorem 34.12 (vertex-cover problem is NP–complete) given in the chapter 34, section 34.5.2 of the textbook.
Refer theorem 34.11 (clique problem is NP–complete) given in the chapter 34, section 34.5.1 of the textbook.
• The vertex-cover problem finds the vertex cover of minimum size in a given graph.
• The clique problem finds a clique of maximum size in a given graph.
• The vertex cover 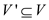 and also
the clique
and also
the clique 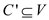 .
.
• The vertex-cover problem and the NP–Complete clique problem are complementary means if the compliment of a graph is considered, then the maximum-size clique in the complement graph is an optimal vertex cover of the graph.
• The clique problem and vertex cover problem are related to each other through a reduction.
• The relation between these two problems does not imply that there exists a constant ratio bound approximation algorithm.
• The reductions may alter the ratio by polynomial times.
Therefore, the reduction relationship between the vertex-cover problem and clique problem doesn’t imply that, for the clique problem, there exists a polynomial-time approximation algorithm with a constant approximation ratio.