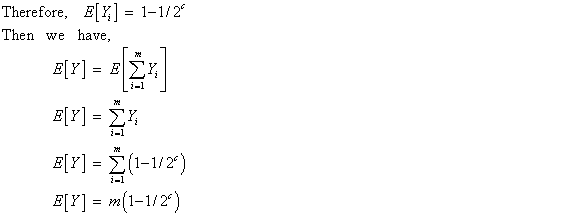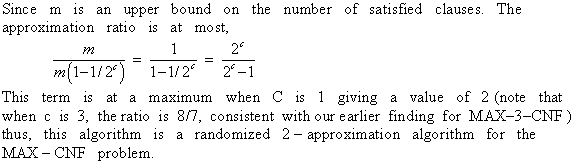MAX-CUT Problem
MAX-CUT problem is the problem in which the vertices of an
undirected graph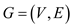 are
partitioned into two parts such that the total weight cut edges are
more than any other cut for the same graph. Weight
are
partitioned into two parts such that the total weight cut edges are
more than any other cut for the same graph. Weight  is a
positive value which is associated with each edge of the graph.
is a
positive value which is associated with each edge of the graph.
For example: Consider the graph G (V,
E), the vertices of which are partitioned into two parts
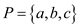 and
and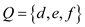 such
that
such
that .
.
In the above graph, for each edge
 and
and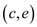 of cut the
vertices
of cut the
vertices 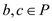 and
and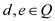 . The weight
of cut is
. The weight
of cut is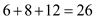 which is the
greater than the weight of any other possible cut of the graph.
which is the
greater than the weight of any other possible cut of the graph.
Now, for the graph G (V, E), proving that a MAX-CUT problem is a randomized 2 approximation algorithm. Randomized approximation algorithms are used for the generation of approximate solutions for the optimization problems. The solutions of randomized algorithm are not of very good quality as they give the average solutions. There are two possible methods that can be used for proving any problem to be the randomized 2 approximation algorithm.
a. De-randomization using conditional expectations.
b. De-randomization using pair-wise independent hashing
a. De-randomization using conditional expectations:
For a graph G (V, E) in which there are
n labels available for vertices, the randomized algorithm
designates a random variable uniformly
from
uniformly
from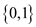 to each
vertex i with the equal probability
to each
vertex i with the equal probability 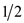 . The cut of
the graph is denoted by
. The cut of
the graph is denoted by .
.
Assume that there are  number of
edges in the cut which is the function of assigned random
variables
number of
edges in the cut which is the function of assigned random
variables . Now for
each edge of
. Now for
each edge of 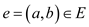 designate
each edge
designate
each edge 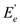 to be 1 if
to be 1 if
 and
and are
different otherwise set it as 0.
are
different otherwise set it as 0.
Since, it is adequate that for a partial assignment then it will
be very easy to calculate the conditional expectation which
is
then it will
be very easy to calculate the conditional expectation which
is .
It is true for each edge
.
It is true for each edge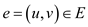 from the
linearity of expectation.
from the
linearity of expectation.
Now, for the conditional expectation there are three cases that should be considered as:
1. If there is no value assigned to variable  and
and
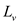 for
vertices u and v then the conditional expectation of
the edge
for
vertices u and v then the conditional expectation of
the edge 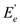 will
be
will
be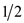 .
.
2. If only one variable in and
and
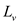 is
assigned the value for the edge e the conditional
expectation
is
assigned the value for the edge e the conditional
expectation 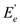 will also
be
will also
be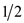 .
.
3. If both the variable and
and
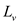 have
a value assigned then the conditional expectation
have
a value assigned then the conditional expectation 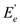 will be 1 if
the values of
will be 1 if
the values of  and
and
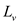 are
different, otherwise it will be 0.
are
different, otherwise it will be 0.
b. De-randomization using pairwise independent hashing:
Pairwise independence means that the probabilistic decisions for
a pair of vertices will be independent of each other. The property
used here from the randomized algorithm is that for every pair of
vertices u, v the probability that u and
v can implement different decision is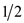 . This
property could be achieved using only
. This
property could be achieved using only 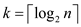 independent
random coin tosses; it cannot be achieved using n
independent random coin tosses.
independent
random coin tosses; it cannot be achieved using n
independent random coin tosses.
Proof for MAX-CUT problem to be a randomized 2 approximation algorithm can be done by any of the above methods.
De-randomization using pairwise independent hashing method:
Consider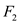 refers to
the field
refers to
the field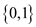 under the
operation of addition and multiplication modulo 2. Assigning value
to each vertex a distance vector
under the
operation of addition and multiplication modulo 2. Assigning value
to each vertex a distance vector 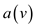 in the
vector space
in the
vector space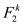 , our choice
of
, our choice
of 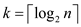 approves that the vector space should allot unique element to each
vertex. Now, assume thatr be a uniform random vector
in
approves that the vector space should allot unique element to each
vertex. Now, assume thatr be a uniform random vector
in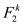 ,
divide all the vertex sets into following subsets:
,
divide all the vertex sets into following subsets:
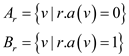
For any edge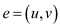 , the
probability that
, the
probability that 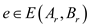 is equal to
the probability that
is equal to
the probability that 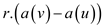 is nonzero.
For any non zero vector that is fixed
is nonzero.
For any non zero vector that is fixed 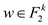 , here is
, here is
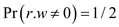 because the
set of r satisfying
because the
set of r satisfying 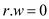 is a linear
subspace of
is a linear
subspace of 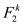 of dimension
of dimension
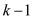 ,
so total
,
so total  of the all
of the all
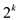 possible
vectors r have zero dot product with wand rest
possible
vectors r have zero dot product with wand rest
 of
them have non zero product with w.
of
them have non zero product with w.
So, if there is a sample  thoroughly
at random, the expected weight of partitions defined by
thoroughly
at random, the expected weight of partitions defined by  is at least
half the weight of the maximum cut. The vector space
is at least
half the weight of the maximum cut. The vector space 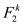 has only
has only
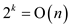 vectors with
itself, which proves to be a deterministic option to our randomized
algorithm.
vectors with
itself, which proves to be a deterministic option to our randomized
algorithm.
Else than selecting r at random, finding out the weight
of the cut  for each
for each

And select the cut which have maximum weight. This is at least as good as selecting r at random.
Therefore, maximum cut problem is a deterministic
2-approximation algorithm with the cost incurred at the running
time with factor of .
.
Linear Programming
Linear programming is a way of achieving the maximum possible outcome from a set of resources that are represented as an integrated mathematical design. In the technical terms the linear programming is a way to achieve optimum results from the linear programming problems. This optimization is subject to a few constraints.
In the single-source shortest-path issue, a shortest path can be found from source vertex s to all the vertices which are present in the graph. In order to do this, for each and every vertex from the considered vertex, the linear programming strategy can be a good choice in which linear equations are formed from the concerned graph.
Standard form of linear program: In a standard form there
is a set of p real numbers that are , another
set of q real numbers that are
, another
set of q real numbers that are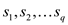 and a set
of
and a set
of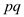 real numbers
that are
real numbers
that are where,
where,
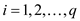
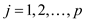
Now, the objective is to find p real numbers such
that
such
that
Maximize
 … … (1)
… … (1)
And that is subject to
 … … (2)
… … (2)
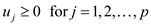 …… (3)
…… (3)
The first expression is called the objective function. The second and the third expression show the constraints. This way a linear program can be put into the standard form.
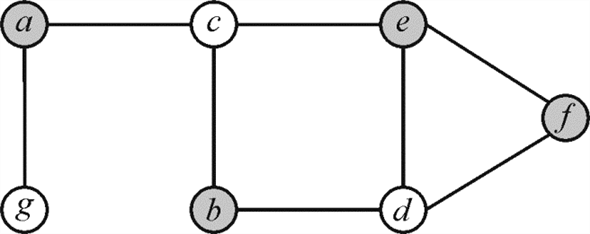
Vertex-Cover: For an undirected graph the vertex cover is
define as the set of vertices that can cover all of the edges of
the concerned graph. Consider the graph  the subset
P of vertex set V is the group of vertices that can
cover all the edges
the subset
P of vertex set V is the group of vertices that can
cover all the edges in the graph
that is either the edge
in the graph
that is either the edge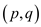 is connected
to vertex a or it is adjacent to the vertex b.
is connected
to vertex a or it is adjacent to the vertex b.
For example: Consider the graph  where
where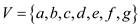 .
.
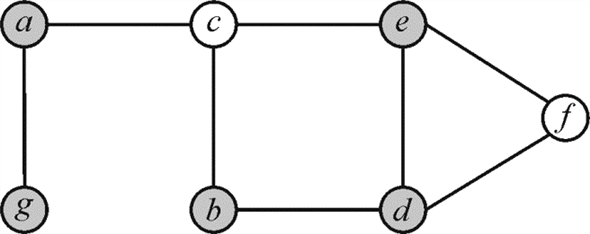
In the above graph the red colored vertices are covering the
edges of graph G that is vertex cover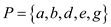 . The size
of vertex cover is the total amount of vertices in the vertex cover
set. For the above graph the size of vertex cover is 4.
. The size
of vertex cover is the total amount of vertices in the vertex cover
set. For the above graph the size of vertex cover is 4.
The vertex cover is called as minimum vertex cover if it contains the minimum number of vertices to cover entire set of edges of the graph that is no more vertices are required.
For example: The minimum cover for the above graph
is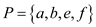 the graph is
shown below:
the graph is
shown below:
The vertex cover of minimum size is also known as optimal vertex cover.
Now, consider the linear-programming relaxation whichis a
linear programming of approximating weighted vertex cover. Consider
an undirected graph G = (V, E) in which
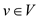 has
an associated positive weight w(v).
has
an associated positive weight w(v).
Now, for any vertex cover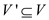 . Define the
weight of the vertex cover.
. Define the
weight of the vertex cover.

To get the vertex cover of least possible weight .Below mention linear program is the
relaxation version for vertex cover of least weight. It is
formed from the 0-1 integer program for getting a minimum weight
vertex cover. If the constraint 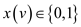 remove from
0-1 integer and replace it by
remove from
0-1 integer and replace it by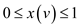 .
.
After replacement, the linear programming version formed is known as linear programming relaxation. Any viable solution of 0-1 integer program in section 35.4, equations (35.14–35.16) is also viable solution to the linear program in equations (35.17–35.20).
Due to this, optimal solution of the linear program gives the lower limit on the value of an optimal solution to the 0-1 linear program, and thus a lower limit on the optimal weight in the minimum-weight vertex cover problem.
Relaxation version of linear programming for minimum weight vertex cover problem is as:
Minimize
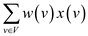 … … (35.17)
… … (35.17)
Subject to
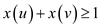 for each
for each
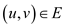 … … (35.18)
… … (35.18)
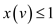 For each
For each 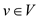 … …
(35.19)
… …
(35.19)
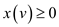 For each
For each 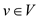 … …
(35.20)
… …
(35.20)
To show that if line (35.19) is removed, from above
program, still there is optimal solution that must satisfy
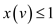 for
each
for
each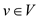 . To solve
the above linear program in polynomial time, assume that
. To solve
the above linear program in polynomial time, assume that  is an
optimal solution to the above linear program. For the optimization
of the program, removing the constraint asked in the problem.
is an
optimal solution to the above linear program. For the optimization
of the program, removing the constraint asked in the problem.
Round every value to the nearest integer,
Set 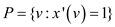
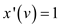 If
If 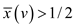
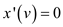 If
If 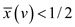
Now, finding the set corresponding to solution x’. The
set P still is a vertex cover; because of every edge
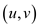 it
is correct that
it
is correct that 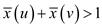 and minimum
one of
and minimum
one of 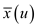 or
or
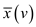 should
be minimum ½ and therefore one of u or v will belong
to P, which is still satisfying the condition of equation
(35.17). The above explanations say that, in a vertex cover
and imagine any edge
should
be minimum ½ and therefore one of u or v will belong
to P, which is still satisfying the condition of equation
(35.17). The above explanations say that, in a vertex cover
and imagine any edge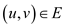 .
.
Now, according to the constraint (35.18) 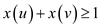 . This
illustrates that at least one of
. This
illustrates that at least one of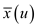 and
and
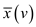 is
at least (1/2).
is
at least (1/2).
Therefore, at least one of u and v is containedin the vertex cover. This means that every edge is covered.
And according to 0-1 linear program, write the constraint that
for any edge (u, v), at least one of u and
v must be in the vertex cover as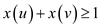 .
.
Hence, it can be said that after removing constraint in equation
(35.19) do not make any sense if these are removed from
linear program, would get the optimal solution which would be
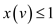 for
each
for
each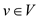 .
.