1E

Maximum sub-array problem on array of negative values

The maximum sub-array problem is to find the sub-array in an array of positive and negative integers, where the sum of the elements of the sub-array is the maximum sum.

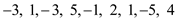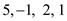For example, consider the array of values. The contiguous sub-array is with the largest sum as 7.

• Assume that the array A contains all negative values.

• In each recursive call, FIND-MAXIMUM-SUBARRAY calls FIND-MAX-CROSSING SUBARRAY.

• FIND-MAX-CROSSING SUBARRAY returns the sum of two sub arrays(cross- sum).

• Since all the values in A are negative, FIND-MAX-CROSSING SUBARRAY always returns a cross-sum (a negative value) that is less than the largest negative value in A.

• In lines 7-11, FIND-MAXIMUM-SUBARRAY compares the left-sum and right-sum with cross-sum and returns corresponding three values.

• Since the largest negative value of A is always greater than the cross-sum, ultimately FIND-MAXIMUM-SUBARRAY returns the largest negative value of A and index of the largest negative value in A.

Therefore, if all the elements of A are negative, then FIND-MAXIMUM-SUBARRAY returns the largest negative value in A and its index.

2E

Maximum sub-array problem

The maximum sub-array problem is to find the sub-array in an array of positive and negative integers, whose elements have the maximum sum.

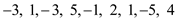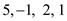For example, consider the array of values. The contiguous sub-array is with the largest sum as 7.

In brute force approach, generate all the possible subarrays combinations and select the one with maximum sum. An array of n numbers has 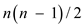subarrays.

Pseudo code for the brute-force method

Input: An array A[1..n] of numbers.

Output: The subarray in an array of n values whose elements have the maximum sum.

S0 ← 0 // the initial prefix sum

for i ← 1 to n do

Si ← Si−1 + A[i]

max ←0 // initializing maximum to 0

// to find the maximum so far

for i ← 1 to n do

for j ← i to n do

if then

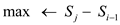
return max

Analyzing the running time of the algorithm

The algorithm examines all consecutive range of elements A[i..j]. For each range, it computes the sum in that range, and update the maximum max if necessary. The number of operations is,

3E

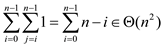
The brute-force and recursive algorithms for the maximum sub-array problem

Consider an example of share market. Suppose a person wants to buy the shares at least possible price and sell them at best possible price to gain maximum profit. But speculating the minimum and maximum price would not be an easy task for a person. This kind of problems can be solved using the maximum sub array approach.

This approach finds out a subarray of a given array that holds consecutive elements of arrayin it and has the largest sum of all the sub arrays in the array. The following algorithms namely, recursive divide and conquer, Brute-Forceare two different ways of implementing the above said concept. Maximum sub array approach would find out the optimal solution for the problems like the one said above.

Brute Force Approach

The algorithm below finds the maximum possible sub array of the array A. Array P holds the maximum possible sum in the first index and starts and end index of the sub-array with maximum sum in the second and third index.

BRUTE-FORCE-ALGORITHM(A, P,n)

//initialize the sum

1. sum:=0

//loop to check the sub-arrays

2. for i=0 to n–1

3. for j=i+1 to n

4. P[0]+= A[j]

//check if the sub array sum is more than the previous sum

5. if(P[0]>sum)

//save the new difference

6. sum=P[0]

//save the buying date

7. P[1]=i

//save the selling date

8. P[2]=j

//return the statistics

9. return P

The brute force algorithm makes the permutation of every single pair of buying and selling prices including the fact that the selling date cannot be earlier or same as the buying date.

Now, the complexity of this algorithm would depend on the size of input. The algorithm would try for every possible combination of any two ascending days. The outer loop would run at least n times and the inner loop will run at most n–1 times. So, the complexity would be:

Brute Force approach works for small number of inputs but becomes tedious and time consuming if the number of inputs increases. In such a case Divide and Conquer approach comes in handy.

Divide-and-Conquer approach

So in the case when number of entries increases recursive algorithm comes into play. Here the divide and conquer rule is used and the complexity of this RECURSIVE-DIVIDE –AND-CONQUER-ALGORITHM is.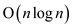

The algorithm is as below in which lb and ub represent the lower and upper bounds of the array A of n entries. The procedure FIND-MAX-CROSSING-SUBARRAY (X, lb, mid, ub) that is used in this procedure is defined in the section 4.1 of the book. Here, lb=1, ub=n initially.

REC-DIVIDE –AND-CONQUER(X, lb, ub)

//base case where the array has only one element

1. if (lb==ub)

2. return (lb, ub, X[lb]);

3. else

//get the new mid-point

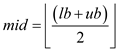
4. //recursive call to the procedure to find the subarrays in the first half

(left-lb, right-ub, left-add) = REC-DIVIDE-AND-CONQUER(X, lb, mid)

//recursive call to the procedure to find the sub array in the second half

5. (right-lb, right-ub, right-add) = REC-DIVIDE-AND-CONQUER(X, mid+1, mid)

//recursive call to the procedure to find the subarrays crossing the mid-point

6. (cross-lb, cross-ub, cross-add) =

FIND-MAX-CROSSING-SUBARRAY(X, lb, mid, ub)

//check if the concerned sub array is found in the first half

7. if left-add>=right-add and left-add>=cross-add

8. return (left-lb, left-ub, left-add)

//check if the sub array is in the second half

9. else if (right-add>=left-add and right-add>=cross-add)

//return the sub array

10. return (right-lb, right-ub, right-sum)

11. else

12. return (cross-add, cross-ub, cross-add)

This algorithm, in general case, is much more efficient than the brute force algorithm. For the base case where there is only one element. The running time would be T(1). The time in dividing the array into smaller sub arrays would be 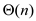as there have to be n divisions.

Now, when merging the array, the time taken would be half of the time taken in dividing the array.

So, it would be.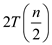

So, the total time would be:

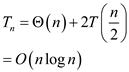
Comparison of performances

Now, have a look at the performances of both the algorithms. Theoretically, it seems that divide and conquer would always perform better than brute force. But practical implementations show that for small inputs the performance of the brute force algorithm is better than the divide and conquer approach. Here is the comparison of both the approaches using the code developed in C#.

/**********************************************************

* Program to compare the brute force and *

* divine-and-conquer approach to find maximum sub array *

**********************************************************/

//namespace system

using System;

namespace max_subarray_prob

{

Create a class that would show the comparison of brute force and the divide-and-conquer approach.

classProgram

{

Date members of the class are the variables that would be used to store the sum and index of the sub-array.

//initialize variables

int m = 0;

int[] p;

int[] q;

int[] s;

Define the brute force function for finding the maximum sub array. This would take as argument the array that the maximum sub-array has to be found within.

/* function to find the maximum sub-array using

Brute force

@param a is the array that the sub-array is to be

Found within

@return the array holding the lower and upper

bounds of the target array */

int[] max_subarray_bruteforce(int[] a)

{

Initialize the variables for storing the information about the sub array.

//initialize variables for storing the indexes

int sub_sum = 0;

int p1 = 0;

int l = 0;

int r = 0;

int max_sum = 0;

Run two nested for loops for finding the lower and the upper bound of the maximum sub array. The outer loop would run till the end of the loop. The inner loop would run from the current value of upper index to the end of the array.

//outer loop to find the sub-array

for (p1 = 0; p1 < a.Length - 1; p1++)

{

sub_sum = 0;

//inner loop that creates the upper bound for the sub-array

for (int p2 = p1; p2 < a.Length; p2++)

{

Store the sum of the subarray in a variable then check if this sum is more than the sum of previous sub array. If so, update the subarray sum and the upper and the lower bound.

//store the sum of sub-array

sub_sum += a[p2];

//check if the sum is more than the previous maximum

if(sub_sum > max_sum)

{

//update the maximum sub-array

max_sum = sub_sum;

l = p1;

r = p2;

}

}

}

Create the subarray and return it.

//create the sub-array

int[] x = { l, r, max_sum };

return x;

}

Define the function to find if the maximum sub array is crossing the crossover point. That means it is partially in the left sub array and rest of it is in the right sub array. The arguments are the concerned array, lower and upper bound and the midpoint of the array.

/* find max sub-array across the crossover point

@Param a is the array that the sub arrays is to be searched @param l lower bound of the array

@param m is the midpoint of the array

@param h upper bound of the array */

int[] crossover_point(int[] a, int l, int m, int

h)

{

Set the initial sum and the indexes.

//set the initial sum and other variables

int left_sum = -1000, right_sum = -1000;

int sum = 0;

int max_left = 0, max_right = 0;

Check if the maximum sub array is in the left sub array.

//loop to find the maximum sub array in the left sub-array

for (int i = m; i >= l; i--)

{

Store the sum of the current sub array and check if it is greater than the previous sum. If so, update the sub array indexes and sum.

//store the sum of the sub-array

sum = sum + a[i];

//check if the left sub array is max

if (sum > left_sum)

{

//update the sub-array bounds

left_sum = sum;

max_left = i;

}

}

sum = 0;

Check if the maximum sub array is in the right half of the array.

//loop to find the max sub array in the right sub- array

for (int j = m + 1; j <= h; j++)

{

Store the sum of the sub array and check if this is greater than the previous. If so, update the subarray indexes and the sum.

//store the sum of the sub-array

sum += a[j];

if (sum > right_sum)

{

right_sum = sum;

max_right = j;

}

}

Create the sub array and return it.

//create the sub-array

int[] y = { max_left, max_right, left_sum +

right_sum };

return y;

}

Define the divide and conquer method for finding the maximum sub array. The arguments are the array, the lower and upper bounds of the array.

/* find the maximum sub array using divide and conquer approach

@Param a is the array that the sub arrays is to be searched

@param l lower bound of the array

@param h upper bound of the array */

int[] max_subarray_dnc(int[] a, int l, int h)

{

Check if there is only one element in the array.

//base case where only one element is there in the array

if (l == h)

{

Return the subarray.

int[] z = { l, h, a[l] };

return z;

}

else

{

Find the new midpoint of the array.

//find the new midpoint of the array

m = (l + h) / 2;

Check the function recursively for left sub array and if the maximum sub array is in that array then return the subarray.

//recursive call to check if the max sub-array is in the left sub array

p = max_subarray_dnc(a, l, m);

Call the function recursively for right sub array and return the sub array if maximum sub array is in that.

//recursive call to check if the max sub-array is in the right sub array

q = max_subarray_dnc(a, m + 1, h);

Call the function to check is the maximum sub array is crossing the crossover point.

//check if the max sub-array is across the crossover point

s = crossover_point(a, l, m, h);

//return the left sub-array

if (p[2] >= q[2] && p[2] >= s[2])

return p;

//return the right sub-array

elseif (q[2] >= p[2] && q[2] >= s[2])

return q;

else

//return the crossover array

return s;

}

}

Define the main() function to call the above defined functions and compare the speed.

//main method

Static void Main()

{

Create the object of the class to call the functions. Initialize the variables.

//create the object

Program pr = newProgram();

//set the array length

int n = 30;

//declare the variables

double time0, time1, time2, time3, t1, t2;

string s1, s2;

int[] x;

int[] a;

Random ran = newRandom();

a = newint[n];

Generate random numbers in a given range and input them in the array.

//input random elements in the array

for (int i = 0; i < n; i++)

a[i] = ran.Next(-20, 20);

Call the functions and calculate the time taken in the execution of each one of them.

//call the brute force method and calculate the time taken

time0 =

Convert.ToDouble(DateTime.Now.ToOADate());

x = pr.max_subarray_bruteforce(a);

time1 =

Convert.ToDouble(DateTime.Now.ToOADate());

Print the array elements.

//print the array

Console.WriteLine("Array is: ");

for (int i = 0; i < n; i++)

Console.Write(a[i] + " ");

Console.WriteLine();

Console.WriteLine();

t1 = time1 - time0;

Print the time taken in the execution of brute force algorithm.

s1= string.Format("{0:0.0000000000000000000000}"

, t1);

Console.WriteLine("brute force: "

+ s1);

//call the divide and conquer method and calculate the time

time2 =

Convert.ToDouble(DateTime.Now.ToOADate());

x = pr.max_subarray_dnc(a, 0, n - 1);

time3 =

Convert.ToDouble(DateTime.Now.ToOADate());

t2 = time3 - time2;

Print the time taken in the execution of divide and conquer algorithm.

s2 =

string.Format("{0:0.0000000000000000000000}"

,t2);

Console.WriteLine("divide and conquer: "

+ s2);

Console.WriteLine();

Console.ReadKey();

}

}

}

Sample Output:

Array is:

-8 -17 0 14 1 -6 18 11 17 15 9 13 -10 -2 -18 -10

-3 -10 -8 -13 18 2 16 -8 11 -14 17 -5 -14 11

brute force: 0.0000000231520971283317

divide and conquer: 0.0000000115687726065516

Various values of array length yield the following results:

Size =

Brute Force Algorithm

Recursive Algorithm

10

0.0000000115760485641658

0.0000000231448211707175

15

0.0000000115687726065516

0.0000000115760485641658

20

0.0000000115760485641658

0.0000000115760485641658

25

0.0000000115687726065516

0.0000000115760485641658

30

0.0000000231520971283317

0.0000000115687726065516

The above results infer that for n0<30 the performance of brute force is better than the divide and conquer one. Keeping this in mind the advantage of brute force can be used in the divide and conquer algorithm so that it can work even faster. The divide and conquer algorithm can be modified to use the brute force algorithm till the time the input size is less than 30.

In the procedure REC-DIVIDE –AND-CONQUER just add the following lines after line 2 to make the changes:

else if (lb==0 and ub<=30)

Initialize a new array P

BRUTE-FORCE-ALGORITHM (X, P, n)

return P

Rest of the algorithm would remain the same. Crossover point would not change even if the problem size is less than n0. The reason is that the crossover point is calculated using the mid of the array and the relative position of mid is not going to be affected by the value of n0. It does not matter how big or small the value of n0 is.

4E

Modification in maximum-sub-array problem

The maximum sub array problem here is a concept where the target is to find the number of days whose combination creates the highest sum of prices, thus the total number of days is taken in an array and the aim is to find a sub array that gives the maximum sum.

Here, the base case of the maximum sub array is defined to be an empty array. The empty array shows its value to be zero but it is not required to show the value of the empty array.

In divide and conquer algorithm, first check if only one value is present in the array, then return that value. If more than one value is present, then take the lower bound in low and upper bound in high and divide the array into two sub arrays.

After that, compare the values of the sub array to find the maximum value in the array and return that value.

This algorithm does not accept an empty array, so we will modify it as:

FIND-MAXIMUM-SUBARRAY ( A, low, high )

// if array is empty

1. for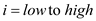

2. if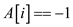

// array is empty

3. return -1

// base case: only one element

4. else if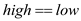

5. return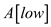

6. else

7.

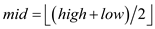
8. FIND-MAXIMUM-SUBARRAY (A, low, mid)

9. FIND-MAXIMUM-SUBARRAY (A, mid+1, high)

10. Compare all three sub arrays to find the max

11. return max

The tiny modification (First “if” section in above algorithm) that is required to be done in this algorithm, is that first check if all the elements of the array are negative, or there is no element in the array, then it returns the value -1 or shows an error message that the array is empty.

Thus, the value displayed for this base case would not result in a zero.

5E

Linear-time algorithm for the maximum-subarray problem:

Consider that the maximum-subarray of A[1..j] is known, and by observation a maximum-subarray of A[1..j +1] is either a maximum-subarray of A[1..j] or a subbarray A[i..j + 1], for some .

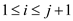Therefore, check from the index j+1 down to 1 to see if a maximum sum is changed or not. If the new maximum sum differs from the maximum sum of maximum-subarray of A[1..j], then maximum-subarray is A[i..j + 1].

Pseudocode:

Find-Maximum-Subarray(A)

// maximum-subarray of A[1..j] is assigned to max-sum

1 max-sum ← A[1..j]

// Initialize sum =0

2 sum = 0

// Initialize i =0

3 i = 0

// check from the index j+1 down to 1

4 for j = j + 1 downto 1

// Add A[j] to sum

5 sum = sum + A[j]

// check whether sum differs maximum-subarray of A[1..j] max-sum

6 if sum > max-sum

7 max-sum = sum

8 i = j

Analysis:

Line 1 initializes the variable max-sum to the maximum-subarray of A[1..j].

Line 2 and 3 initializes the variables sum and i.

Thus, lines 1-3 takes the constant time T(1) = Θ(1).

Lines 4-8 use for loop to ◊nd the new sum from j+1 down to 1. So, it takes the running time of T (j) = Θ(j), j > 0.

Thus, the algorithm takes a linear- time running for the maximum-subarray problem.

Chegg Rip, Introduction to Algorithms, 3rd Edition. [RipVer 0.1] (index)