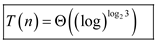Solving Recurrences

The specified recurrence is below:

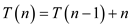
Guess the solution as .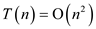

Use the substitution method to prove that the guess is correct.

So, have to prove that 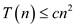for a constant c, where.

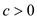From the guess,

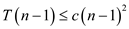
Using the Substitution Method:

Substitute the guess in the recurrence, then

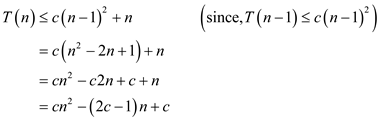
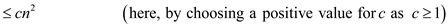
Finding Boundary Conditions using Mathematical Induction:

Assume that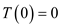

For n = 1,

From the specified recurrence,

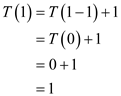
And from the inequality,

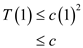
Therefore, 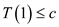for

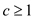
For n = 2,

From the specified recurrence,

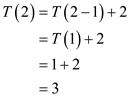
And from the inequality,

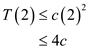
Therefore, 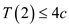for

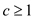
For n = 3,

From the specified recurrence,

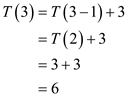
And from the inequality,

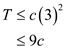
Therefore, 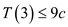for

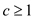
Therefore, 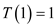, 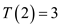and 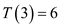by choosing the value of c as .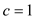

Since, the recurrence is true for base case 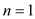, , 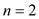and 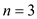; by the mathematical induction the given recurrence is true for all values of .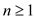

Thus, .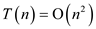

The following steps are used for solving recurrences:

The specified recurrence is as shown below:

•

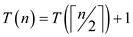
Guess the solution as,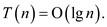

Use Substitution method to prove that the guess is correct.

Prove that 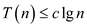for a constant c.

Here,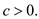

From the guess, the following is ascertained:

•

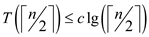
The following steps are used to substitute the guess in the recurrence as shown below:

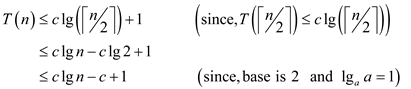
This inequality is not conclusive, still 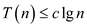for a positive value of c.

Prove that.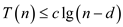

Here, d is a constant.

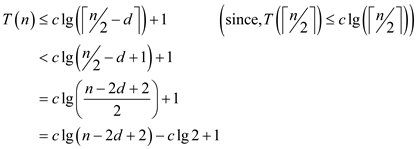
The following steps are used to find the boundary conditions using Mathematical Induction:

The inequality, 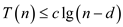does not work for n = 1 and n = 2 because 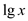cannot be defined for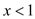, since 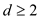and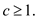

Assume, 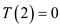and

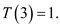
Calculate, for n = 4 as shown below:

From the specified recurrence,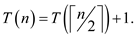

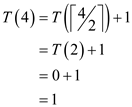
From the inequality, the following can be ascertained:

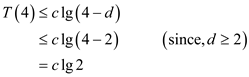
Therefore, 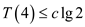for

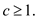
The following steps are used to calculate for n = 5 as shown below:

From the specified recurrence,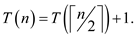

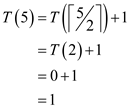
From the inequality, the following can be ascertained:

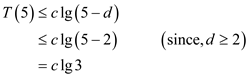
Therefore, 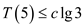for

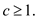
Calculate, for n = 6 as shown below:

From the specified recurrence,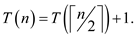

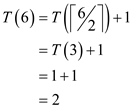
From the inequality, the following can be ascertained:

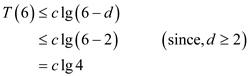
Therefore, 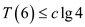for

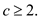
The following steps are used to calculate for n = 7 as shown below:

From the specified recurrence,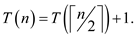

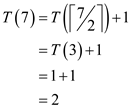
From the inequality, the following can be ascertained:

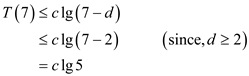
Therefore, 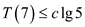for

The following steps are used to calculate for n = 8 as shown below:

From the specified recurrence,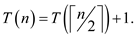

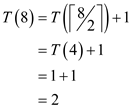
From the inequality, the following can be ascertained:

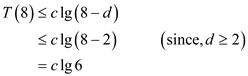
Therefore, 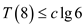for

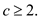
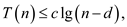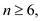
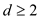Therefore, the recurrence is true by the mathematical induction for the inequality for all values of and

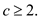
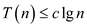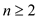So, the recurrence is true by the mathematical induction for the inequality for all values of and

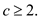
Thus, .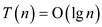

Substitution method for solving recurrences

• It is already proved in the text book that the solution of 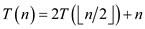is 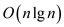. Also , it is known that Big-O gives the asymptotic upper bound.

• Now, it is to be proved that the solution of 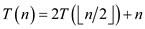is also 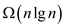. 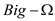provides the asymptotic lower bound.

Proving 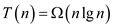using Substitution method:

• To prove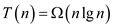, make a guess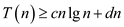. Where d is a positive constant.

• Now, substitute the in the given recursion relation.

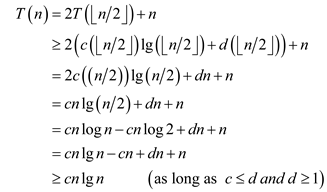
Finding constants using mathematical induction:

• For base case, prove

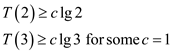
• Assume.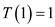

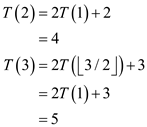
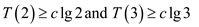• are true for

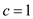
• Since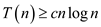, by the definition of ,

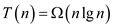
Therefore, the solution of the recurrence relation 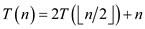is .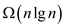

Proving that also :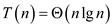

• According to the definition of big-,, if and only if 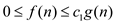and 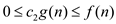for some positive constants .

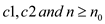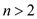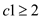• Since it is already proved that and for, and, .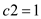

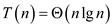Therefore, it can be concluded that the solution of the recurrence relation 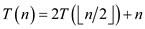is .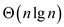

Consider the following inductive hypothesis, which is used to overcome the problem with the boundary condition 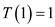for the given recurrence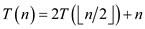, without adjusting the boundary condition.

Now, suppose that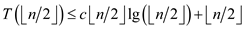. Then, to overcome the above problem, user has to prove that.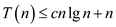

Hence,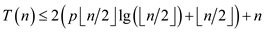

Where, denotes the floor value.

Now, simplify the above expression as shown below:

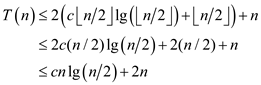
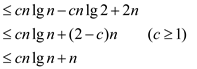
Now, the boundary condition is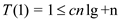

Therefore, from the above calculation, user can select any value 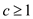such that the inductive and base steps are true.

Hence, it can be concluded that,.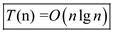

Recurrence Relation of Merge Sort

Consider the following recurrence relation of merge sort:

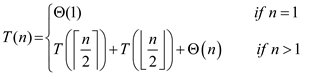
Now, prove that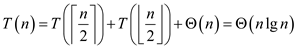

For a given function g(n),

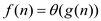, where there exist constants c1, c2 and such that:

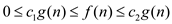for all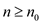

It means that g(n) is an asymptotically tight bound for f(n) if it can be proved that :

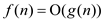and .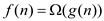

So, the complexity of the merge sort can be proved to be 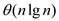if :

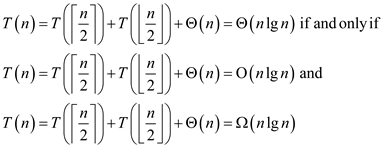
Let and 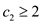, by inductive hypothesis assume true for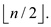

Hence,.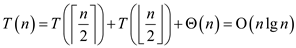

, by inductive hypothesis assume true for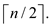

Hence,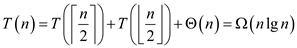and

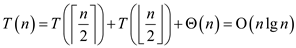
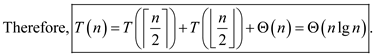
Solving recurrence relation using substitution method:

In the substitution method a solution is gussed every time and checked whether it is working or not.

Consider the following given recurrence relation:

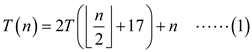
Now, solve the recurrence relation using substitution method, by making a guess that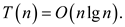

Since substitution method is employing, it is required to prove that

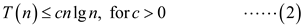
Thus, also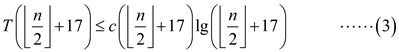

Substitute (3) in (1).

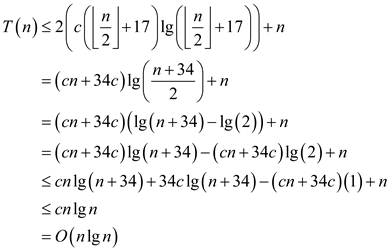
Therefore,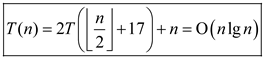

Master method:

Consider the following recurrence relation:

Consider the master theorem for the recurrence equation:

By comparing equation (1) and (2), the value a=4, b=3, c=1,.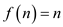

Using the master method, simply apply case 1 of the master theorem.

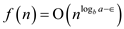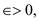If for some constant then

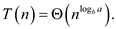
Therefore,.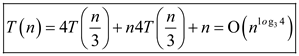

Substitution Method:

Consider the following recurrence relation:

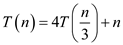
Assume the initial guess as.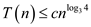

Then,

Substitute equation (3) in the equation (1)

As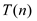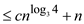, the guess 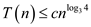fails.

Now again guess

Substitute equation (4) in the equation (1).

As 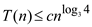, the guessis true.

Therefore,.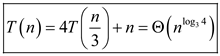

Using Master method:

Proof for the solution to the recurrence 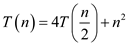is 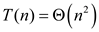shown below:

Consider the following recurrence relation:

Consider the master theorem for the following recurrence equation:

By comparing equations (1) and (2), the value a=4, b=2, c=2, and.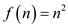

Using the master method, apply case 1 of the master theorem.

The case 1 of the master theorem is shown below:

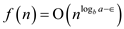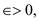If for some constant, then

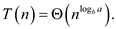
Therefore, by using the master method the solution for the given recurrence relation is .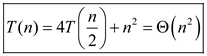

Using Substitution Method:

Proof that the assumption 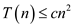fails using substitution method is shown below:

Consider the following recurrence relation:

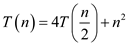
Solve the recurrence relation by using substitution method.

Assume the initial guess as.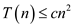

Then,

Hence, fails to be less than 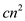for any .

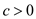Therefore, for the assumed initial guess 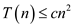, the obtained solution is.

Hence, the guess 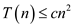fails by using the substitution method.

Now, again make a guess to subtract off a lower-order term to make the substitution proof work.

Solve the recurrence relation by using substitution method.

Then, the guess is 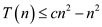, it means that the lower term which is subtracted from 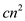is .

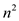Then,

Therefore, for the assumed guess 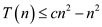, the obtained solution, 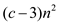is less than .

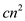Hence, the guess 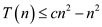is true by using the substitution method.

Therefore, by using the substitution method the solution for the given recurrence relation is , .

Consider the recurrence relation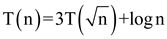

The recurrence is solved by change of variables and for convenience don’t worry about integral values, such as 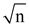to be an integer. Renaming m = lg n yields

Let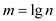

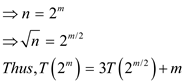
Now rename 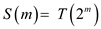to produce the new recurrence

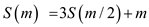
Where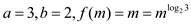

Since the value of 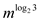in between 1 and 2

Apply case 1 of master theorem then the new recurrence has same solution

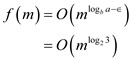
Thus,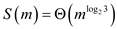

Changing back from 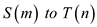then we obtain

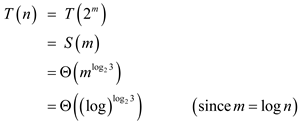
Thus, the running time