The identity permutation is defined as the permutation of given
numbers in their natural order. The identity permutation of first
natural number is given as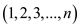 
. Also, it
is known that n! permutations are possible with n
numbers.
• Now, consider the given PERMUTE-WITHOUT-IDENTITY algorithm. Using this algorithm Professor Kelp wants procedure at random any permutation besides the identity permutation.
• That is , the Professor kelp wants to produce any one of all possible permutations(n!) of array of n elements, except the identity permutation(i.e. 1,2,3,….n).
• Thus the PERMUTE-WITHOUT-IDENTITY algorithm must produce any one of the n!-1 permutations.
The given PERMUTE-WITHOUT-IDENTITY algorithm will not produce the identity permutation, also it fails to produce some other permutations.
Now consider the PERMUTE-WITHOUT-IDENTITY algorithm for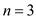
. So, for
,
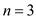the total number of permutation besides identity permutation will be calculated as:
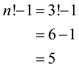
That is, the PERMUTE-WITHOUT-IDENTITY algorithm must produce 5 random permutations besides the identity permutation.
For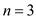, the for
loop, in the PERMUTE-WITHOUT-IDENTITY algorithm, iterates for
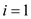and
.
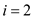For first iteration (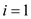
):
• When,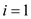, the
RANDOM(2, 3) function will return the values either 2 or 3.
• Thus, only two permutations are possible in the first iteration.
For second iteration (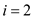
):
• When,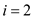, the
RANDOM(3, 3) function will return only a single value which is
3.
• Thus, only one permutation is possible in the second iteration. Also this permutation can be produced in iteration one.
Therefore for n=3, the total number of possible permutation produced by PERMUTE-WITHOUT-IDENTITY algorithm is 2 rather than the 5 permutations.
Hence, the PERMUTE-WITHOUT-IDENTITY algorithm does not produce what Professor Kelp intended.
Consider the given PERMUTE-BY-CYCLIC algorithm.
• 1st line initializes a variable n with the size of array A.
• 2nd line declares an empty array B to store permuted elements of array A.
• 3rd line generates a random number between 1 and n and stores in offset.
• 4th line implements a for loop to permute elements of A by storing them in B at different positions.
• 5th line adds i to offset and stores the result into dest.
• 6th line checks the index value dest is greater than n or not. If condition is true, then resets the value of dest by performing modular division.
• 8th line stores the ith element of A into B at position dest.
The PERMUTE-BY-CYCLIC algorithm randomly selects a value between 1 and n as offeset. The index dest is determined by adding i to offset. If dest is greater than n, dest is updated by perfoming modular divisionon dest with n( dest=dest-n or dest= dest % n). This procedure generates a cyclic rotation of the array.
However, each time, the value of dest is between 1 to n. Thus, each element of A may save at any one of n positions (indexes) of B. Therefore, the probability of an element A[i] to store at one position of B is 1/n.
An algorithm is said to be produces uniformly random permutations on a set of n elements, if the algorithm can produce n! random permutations with each permutation is equally likely to appear( That is, each permutation should have probability 1/n!).
Therefore, the PERMUTE-BY-CYCLIC algorithm does not produce uniform random permutation, because it determined only one offset(one random number) for whole permutation with probability 1/n. Hence, it only generates n random permutations. Each of these random permutations is occurred with probability of 1/n.
Hence, PERMUTE-BY-CYCLIC algorithm does not produce uniform random permutation.
Consider the algorithm PERMUTE-BY-SORTING(). To increase the
uniqueness, randomly choose the elements of array P between 1
to
.
Here, n is the size of the array P.
• For value of i, j such that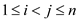
, Consider
that will denote that an element at index i and j are identical, in
array P.
• Since elements in P are chosen independently at random from
values 1 to, the
probability that an element at index i and j are identical in array
P,
Finding the probability that all elements are unique in array P:
• Assume, if elements at first i-1 index are unique, then
the probability that the element at index i is unique,
Pr{Ei} 
. …… (1)
• Therefore, the probability that all elements are unique is
…… (2)
• From equation (1) and (2), the above expression can be written as,
• This can be further solved to,
Hence, the probability that all elements are unique is at
least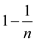
.
Producing uniform random permutation
Consider the PERMUTE-BY-SORTING () algorithm that permutes the elements of array A by random priorities. Where, A is an array of n elements. The PERMUTE-BY-SORTING () algorithm may possibly generate or assign same priority to one or more elements in the array A. The algorithm can be modified such that the algorithm produces a uniform random permutation.
Now, consider the following modified algorithm of PERUMTE-BY-SORTING that produces a uniform random permutation.
MODIFIED-PERMUTE-BY-SORTING (A)
//Determine number of elements in the array A
1. 
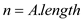
2. let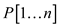 
be new
array
//initialize the array P with numbers, 1 through n.
3. for 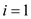to
n
4. 
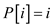
5. for 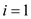to
n
//choose a random number between 1 and n
6. k = RANDOM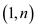
//swap the ith and kth elements of P so that no two priorities are not same.
7. SWAP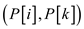
8. Sort A using priorities in P as sort keys
Uniform random permutation is achieved by assigning the priorities in increasing order 1 through n and in each iteration swapping the ith element and kth elements in P. Where, k is the random number chosen in the range 1 to n.