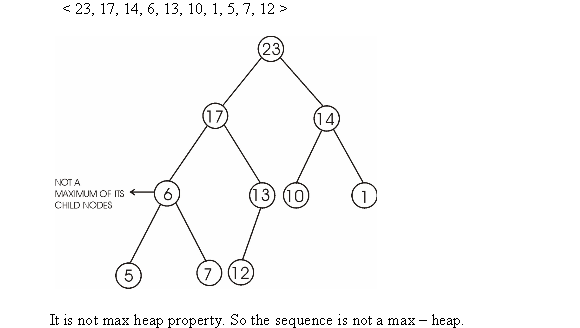
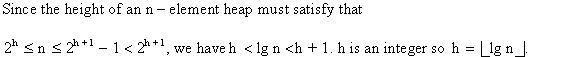A max-heap is an array of elements such that the max-heap can be viewed as a nearly complete binary tree.
Properties of max-heap tree:
• If  is the
max-heap array, then root of the max-heap is stored at
A[1].
is the
max-heap array, then root of the max-heap is stored at
A[1].
• Parent, left child and right child of a node ‘i’ can be
obtained by indexes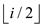 ,
,  and
and
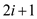 respectively.
respectively.
• Max-heap property ensures that parent node must be larger than
or equal to its children. i.e. 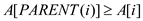 .
.
• In the array , every node
of index
, every node
of index 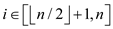 is a leaf
node in the max-heap tree and every node of index
is a leaf
node in the max-heap tree and every node of index 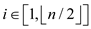 is an
internal node of max-heap tree.
is an
internal node of max-heap tree.
Now it is to be proved that root node of any sub tree of max-heap contains the largest value in that sub tree.
Consider the following proof that shows that root node of any sub tree of max-heap contains the largest value in that sub tree:
Base case ( if a node is leaf node):
• Consider a node L such that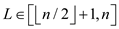 .
.
• That is, 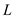 is a leaf
node of a max-heap.
is a leaf
node of a max-heap.
• Since L is the sub-tree rooted at 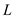 , just
L contains single node.
, just
L contains single node.
• Thus, obviously node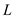 contains the
largest value in that sub-tree.
contains the
largest value in that sub-tree.
Inductive case (if a node is an internal node):
• Consider a node L such that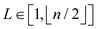 .
.
• That is, 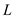 is an
internal node of a max-heap.
is an
internal node of a max-heap.
• Assume that 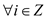 such
that
such
that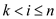 ,
, 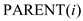 is true.
That is, these node are leaf nodes and they have parent nodes.
is true.
That is, these node are leaf nodes and they have parent nodes.
• Also, since these nodes are leaf nodes(sub trees having single node), these nodes contain the largest value occurring anywhere in that sub-tree.
Now consider the node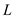 :
:
• 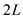 and
and
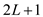 are
the left and right child of node L respectively.
are
the left and right child of node L respectively.
• Since 2L and 2L+1 are child nodes, they contain
the largest value, by the inductive hypothesis that for 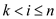 ,
, 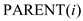 is true.
is true.
• Now, because of the max-heap property, parent node L must contain larger value than the value that the left child 2L and right child 2L+1 have.
• So, it can be concluded that the node 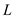 contains the
largest value in the sub-tree rooted at
contains the
largest value in the sub-tree rooted at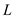 .
.
Therefore it is proved that root node of any sub tree of max-heap contains the largest value occurring anywhere in that subtree.
In the max-heap, the maximum element will be the root node. In other words, root element in the max-heap is greater than or equal to the elements of its children.
• If the elements in the max-heap are distinct, then root element in the max-heap will be greater than the elements of its children.
• All the smaller elements will be in the leaf nodes.
• The smallest element resides in one of the leaf nodes of the max-heap.
Assume that the number of elements in a max-heap is n. As
all the elements are distinct, the indices of the elements start
from 1 and end at n. Then the indices of the leaf nodes are
starting from 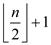 and ending
with n. Therefore, the index of the smallest in the max-heap
lies in the indices
and ending
with n. Therefore, the index of the smallest in the max-heap
lies in the indices 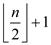 and
n.
and
n.
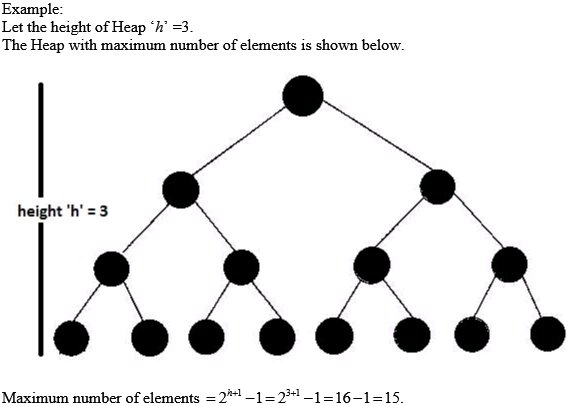
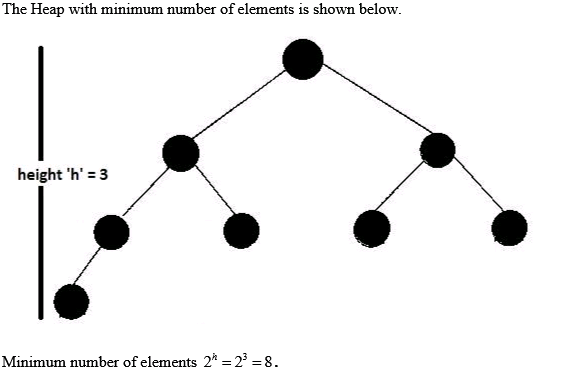
Example of a max-heap:
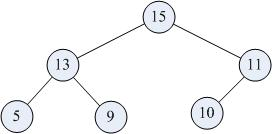
In the above example, the maximum element is 15 which is the root element and the smallest element is 5 which is one among the leaf nodes.
Therefore, the smallest element in the max-heap exists in one of the leaf nodes of the max-heap.
In a sorted array, say A, the element at index i will be
less than or equal to the element at index j for
i<j. That is 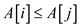 for
i<j.
for
i<j.
If a sorted array is represented as min-heap, then the node at
index i will be the parent node and nodes at index 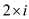 and
and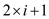 will be its children. Both the children are greater than the parent
and hence they satisfy the property of min-heap.
will be its children. Both the children are greater than the parent
and hence they satisfy the property of min-heap.
Hence, the array that is in a sorted order is a min-heap.
Following is an example of sorted array:
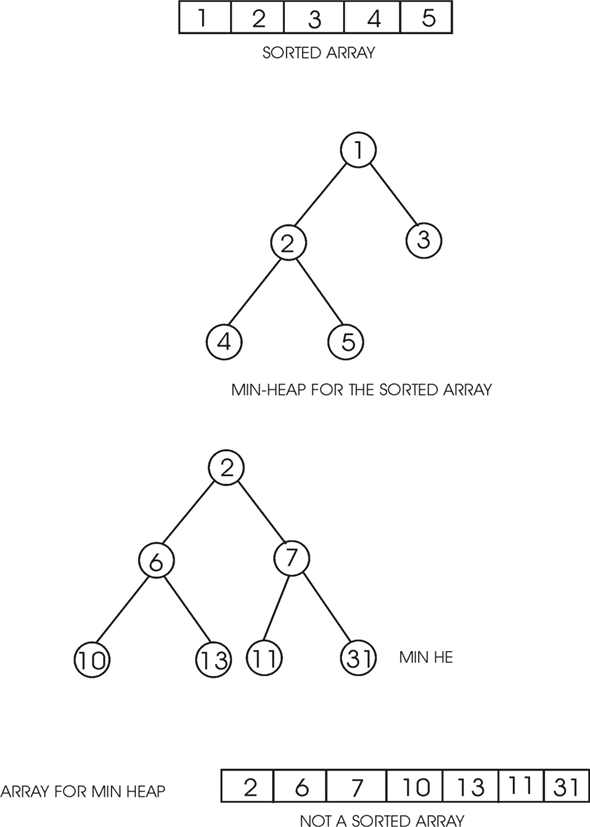
Min-heap for the sorted array is shown below:
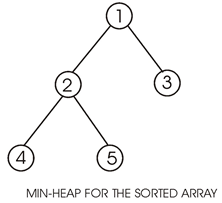
Heap:
Heap data structure is a tree and it is generally represented by an array X where value for each node of heap is represented as an element of X.
• Every node in the heap must be satisfying the heap property. If the heap is max-heap, the value of every node must be less than or equal to its parent’s value. If the heap is min-heap, the value of every node must be greater than or equal to the value of its parent’s value.
• Always X [1] be the root of the tree.
• If the parent is stored at index i, then the left child will be stored at index 2i.
• If the parent is stored at index i, then the right child will be stored at index 2i +1.
• Suppose the root is at index i, then the children for this root node will be at 2i + 1, 2i + 2…..2i + n. where n is the number of elements in the heap.
Indexes of leaf nodes in the heap:
• Consider an n-element heap. Now it is to be proved that
the leaves of the n-element heap are stored in the array
from indexes 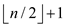 to
to .
.
• Assume that a non-leaf node is stored at index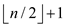 . Now check
the index of left child of non-leaf node indexed at
. Now check
the index of left child of non-leaf node indexed at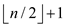 .
.
• From the definition of the heap , LEFT(i)= 2i
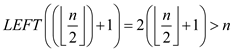
• From the definition of the heap , RIGHT(i)= 2i+1
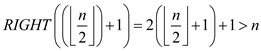
• It is observed that, if a non-leaf node is stored at 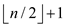 or index
greater than
or index
greater than 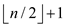 , then the
index of its left child and right exceed the total number of
elements(n). That is the indexes are out of bounds of the
array. Thus this is against the definition of heap.
, then the
index of its left child and right exceed the total number of
elements(n). That is the indexes are out of bounds of the
array. Thus this is against the definition of heap.
• Therefore, non-leaf nodes can be stored only up to
index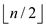 . Thus the
elements from the indexes
. Thus the
elements from the indexes 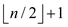 to
to  are leaf
nodes.
are leaf
nodes.
So, the leaves of the n -element heap,
in array representation, are indexed by the 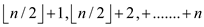 .
.
Example:
Consider the following 10-element heap and its array representation
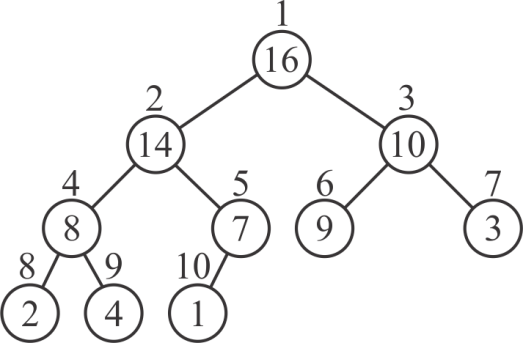

• Where n=10
• Values of non-leaf nodes: 16,14,10,8,7 (indexed from 1 to 5)
• Values of leaf nodes: 9, 3, 2, 4, 1 (indexed from 6 to 10).