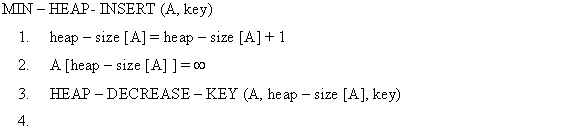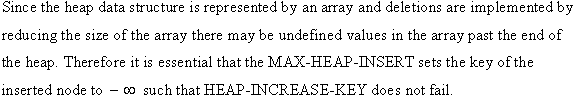Extracting Maximum from Heap
The following heap  is
constructed with the specified set of elements.
is
constructed with the specified set of elements.
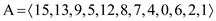
The size of this heap: 12
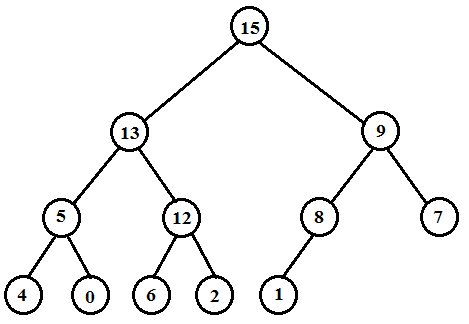
The maximum element of the above heap is 15. So, the HEAP-EXTRACT-MAX operation extracts and returns the element 15 from the heap. Then the MAX-HEAPIFY operation rearranges the elements to satisfy the max-heap property.
Steps Involved:
• Extract the maximum element 15 from the root
• Move the value 1, which is at the last node, to the root
• Swap 1 and 13
• Swap 1 and 12
• Swap 1 and 6
• Remove the last node
Therefore the new heap is as below.
Now, 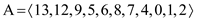
The size of this heap: 11
The extracting elements (in extracting order): 15
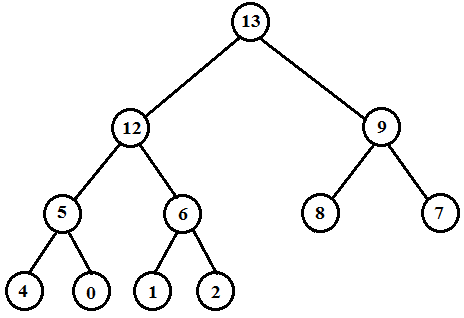
The maximum element of the above heap is 13. So, the HEAP-EXTRACT-MAX operation extracts and returns the element 13 from the heap. Then the MAX-HEAPIFY operation rearranges the elements to satisfy the max-heap property.
Steps Involved:
• Extract the maximum element 13 from the root
• Move the value 2, which is at the last node, to the root
• Swap 2 and 12
• Swap 2 and 6
• Remove the last node
Therefore the new heap is as below.
Now, 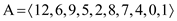
The size of this heap: 10
The extracting elements (in extracting order): 15, 13
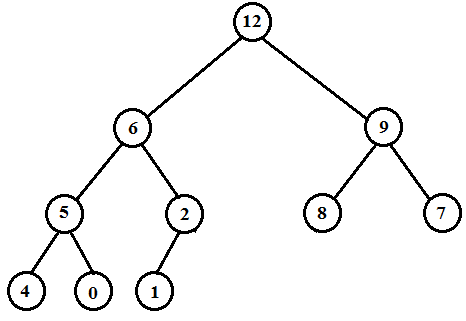
The maximum element of the above heap is 12. So, the HEAP-EXTRACT-MAX operation extracts and returns the element 12 from the heap. Then the MAX-HEAPIFY operation rearranges the elements to satisfy the max-heap property.
Steps Involved:
• Extract the maximum element 12 from the root
• Move the value 1, which is at the last node, to the root
• Swap 1 and 9
• Swap 1 and 8
• Remove the last node
Therefore the new heap is as below.
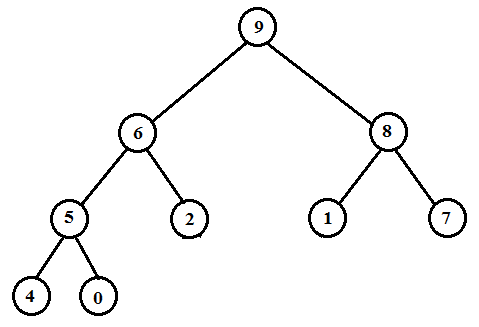
Now, 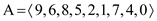
The size of this heap: 9
The extracting elements (in extracting order): 15, 13, 12
The maximum element of the above heap is 9. So, the HEAP-EXTRACT-MAX operation extracts and returns the element 9 from the heap. Then the MAX-HEAPIFY operation rearranges the elements to satisfy the max-heap property.
Steps Involved:
• Extract the maximum element 9 from the root
• Move the value 0, which is at the last node, to the root
• Swap 0 and 8
• Swap 0 and 7
• Remove the last node
Therefore the new heap is as below.
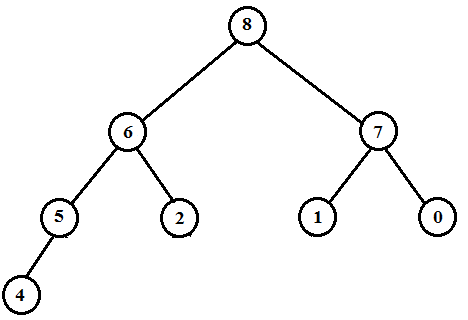
Now, 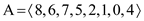
The maximum element of the above heap is 8. So, the HEAP-EXTRACT-MAX operation extracts and returns the element 8 from the heap. Then the MAX-HEAPIFY operation rearranges the elements to satisfy the max-heap property.
Steps Involved:
• Extract the maximum element 8 from the root
• Move the value 4, which is at the last node, to the root
• Swap 4 and 7
• Remove the last node
Therefore the new heap is as below.
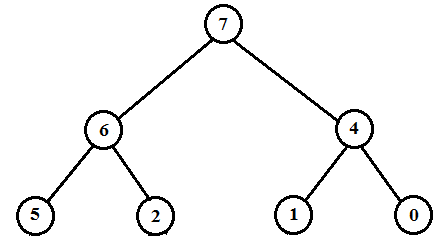
Now, 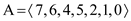
The size of this heap: 7
The extracting elements (in extracting order): 15, 13, 12, 9, 8
The maximum element of the above heap is 7. So, the HEAP-EXTRACT-MAX operation extracts and returns the element 7 from the heap. Then the MAX-HEAPIFY operation rearranges the elements to satisfy the max-heap property.
Steps Involved:
• Extract the maximum element 7 from the root
• Move the value 0, which is at the last node, to the root
• Swap 0 and 6
• Swap 0 and 5
• Remove the last node
Therefore the new heap is as below.
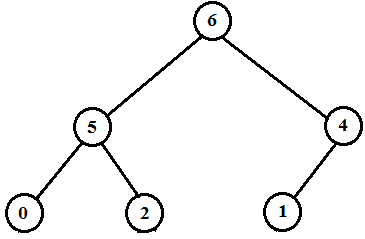
Now, 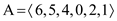
The size of this heap: 6
The extracting elements (in extracting order): 15, 13, 12, 9, 8, 7
The maximum element of the above heap is 6. So, the HEAP-EXTRACT-MAX operation extracts and returns the element 6 from the heap. Then the MAX-HEAPIFY operation rearranges the elements to satisfy the max-heap property.
Steps Involved:
• Extract the maximum element 6 from the root
• Move the value 1, which is at the last node, to the root
• Swap 1 and 5
• Swap 1 and 2
• Remove the last node
Therefore the new heap is as below.
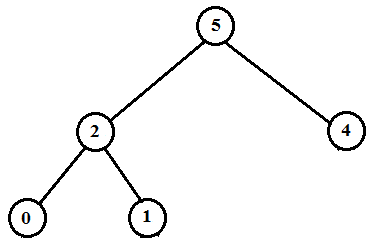
Now, 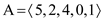
The size of this heap: 5
The extracting elements (in extracting order): 15, 13, 12, 9, 8, 7, 6
The maximum element of the above heap is 5. So, the HEAP-EXTRACT-MAX operation extracts and returns the element 5 from the heap. Then the MAX-HEAPIFY operation rearranges the elements to satisfy the max-heap property.
Steps Involved:
• Extract the maximum element 5 from the root
• Move the value 1, which is at the last node, to the root
• Swap 1 and 4
• Remove the last node
Therefore the new heap is as below.
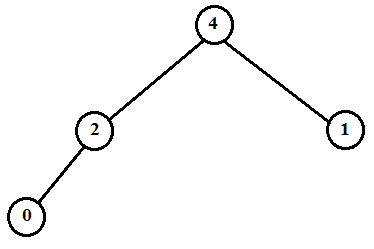
Now, 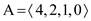
The size of this heap: 4
The extracting elements (in extracting order): 15, 13, 12, 9, 8, 7, 6, 5
The maximum element of the above heap is 4. So, the HEAP-EXTRACT-MAX operation extracts and returns the element 4 from the heap. Then the MAX-HEAPIFY operation rearranges the elements to satisfy the max-heap property.
Steps Involved:
• Extract the maximum element 4 from the root
• Move the value 0, which is at the last node, to the root
• Swap 0 and 2
• Remove the last node
Therefore the new heap is as below.
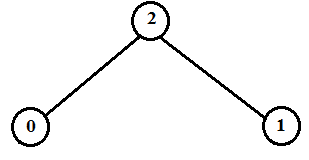
Now, 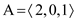
The size of this heap: 3
The extracting elements (in extracting order): 15, 13, 12, 9, 8, 7, 6, 5, 4
The maximum element of the above heap is 2. So, the HEAP-EXTRACT-MAX operation extracts and returns the element 2 from the heap. Then the MAX-HEAPIFY operation rearranges the elements to satisfy the max-heap property.
Steps Involved:
• Extract the maximum element 2 from the root
• Move the value 1, which is at the last node, to the root
• Remove the last node
Therefore the new heap is as below.
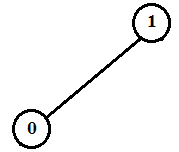
Now, 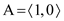
The size of this heap: 2
The extracting elements (in extracting order): 15, 13, 12, 9, 8, 7, 6, 5, 4, 2The maximum element of the above heap is 1. So, the HEAP-EXTRACT-MAX operation extracts and returns the element 1 from the heap. Then the MAX-HEAPIFY operation rearranges the elements to satisfy the max-heap property.
Steps Involved:
• Extract the maximum element 1 from the root
• Move the value 0, which is at the last node, to the root
• Remove the last node
Therefore the new heap is as below.

Now, 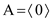
The size of this heap: 1
The extracting elements (in extracting order): 15, 13, 12, 9, 8, 7, 6, 5, 4, 2, 1The maximum element of the above heap is 0. So, the HEAP-EXTRACT-MAX operation extracts and returns the element 0 from the heap. Then the MAX-HEAPIFY operation rearranges the elements to satisfy the max-heap property.
Steps Involved:
• Extract the maximum element 0 from the root
• Remove the last node
Therefore the new heap is empty.
The size of this heap: 0
The extracting elements (in extracting order): 15, 13, 12, 9, 8, 7, 6, 5, 4, 2, 1, 0
The following heap, 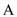 is
constructed with the specified set of elements
is
constructed with the specified set of elements 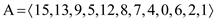
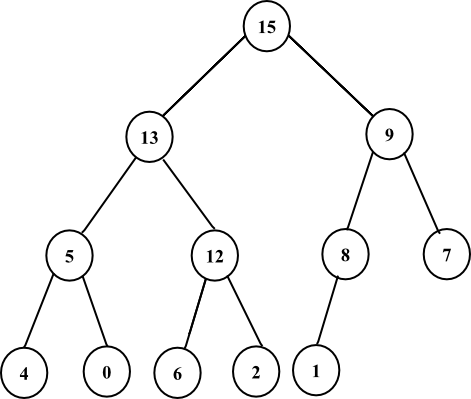
Insert 10 as the last node. After inserting, the tree is as follows:
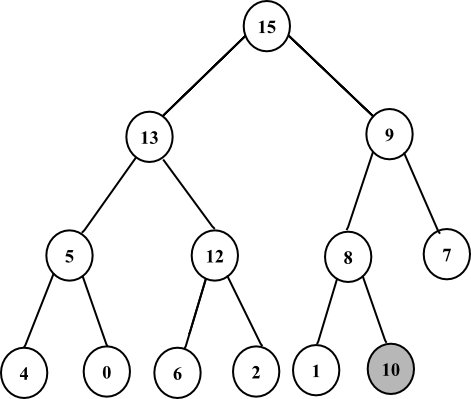
As the parent of node 10, which is 8 is less than 10, exchange the nodes 8 and 10. After exchanging, the tree is as follows:
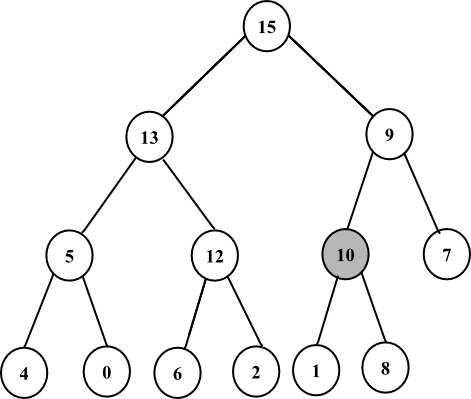
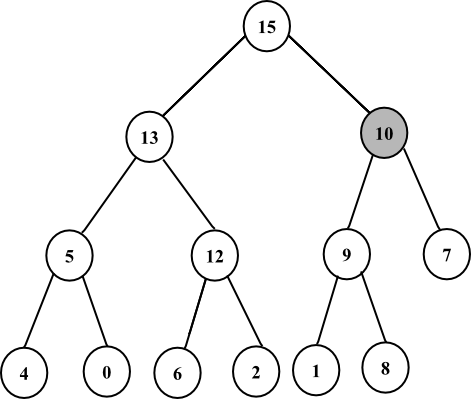
As the parent of node 10 which is 15 is greater 10, no exchange takes place.
Hence, the final heap is as shown below:
Consider the HEAP-INCREASE-KEY algorithm provided in the textbook which needs three assignments in its line number 5. These three assignments are reduced using the concept of inner loop of INSERTION-SORT.
In HEAP-INCREASE-KEY algorithm the exchange operation used in line number 5 requires three assignments.
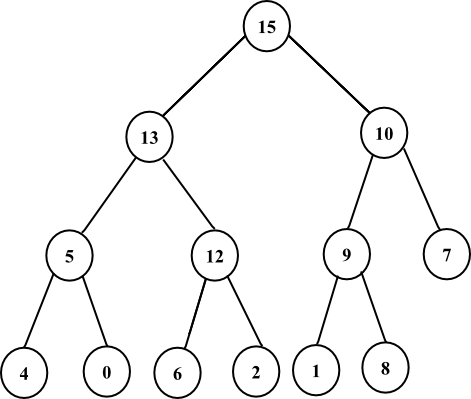
• In first step assign the value of  in a
temporary variable named temp.
in a
temporary variable named temp.
• In second step assign the value of 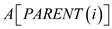 to
to

• In third step assign the value of temp to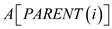 .
.
Following three steps are used to swap the value:
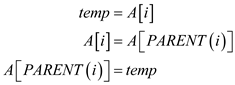
These three assignments are necessary for the exchange of variables but they can be reduced to just one assignment by using the concept of the inner loop of insertion sort.
while loop is used in line no. 4 of algorithm will reduce the three assignments to one assignment as illustrated below:
HEAP-INCREASE-KEY (A, i, key)
//check the value of key
1. if 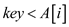
//display the error message.
2. error "new key is smaller than current key"
//assign the value of key in ith location of array A.
3. 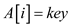
//while loop is used to check the value of index i and compare the value of A[i] to its
//parent.
4. while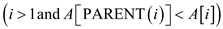
//sift the value of parent to its child
5. 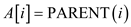
//copy the parent node value into i.
6. 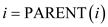
7. 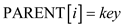
Explanation of Algorithm:
• In line 5 of the above algorithm shift the value of the parent node to its child till the parent value is less than the child value.
• When while loop used in line no. 4 breaks, assign the key value to the parent.
• In this way reduce the 3 assignments of line no. 5 to just one assignment.
HEAP-DELETE can be implementead as HEAP-EXTRACT-MAX. First swap the last value in the array with the item in the node i. Then decrease the heap size by 1. Finally, to maintain max-heap property , call MAX-HEAPIFY.
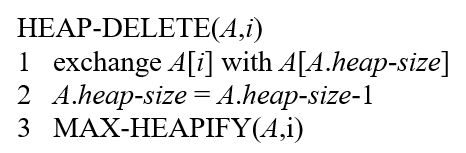
Run time for HEAP-DELETE:
• All lines except the line 3 runs in constant time.
• In each call of MAX-HEAPIFY, it determines the largest between left and right of node i. Then swaps the largest value with item in node i. MAX-HEAPIFY called recursively until the max-heap property is achieved.
• Thus the MAX-HEAPIFY runs O(lg n) time.
Therefore, the HEAP-DELETE( A , i ) also runs in O (lg n ) time.
Consider the min-heap property of min-heap. According to this property, “every node except the root node consists its value minimum as much as that of its parent node”.
So, the minimum value in all the elements is acquired by the root node of the min-heap.
Now consider the following:
BUILD-MIN-HEAP:
It is used to create a min-heap using  elements. It
takes a time complexity of
elements. It
takes a time complexity of 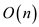 to build
this min-heap.
to build
this min-heap.
HEAP-MINIMUM:
It is used to return the minimum of all the elements exists in
the heap. It takes a time complexity of 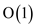 to return
the minimum of all the elements.
to return
the minimum of all the elements.
MIN-HEAPIFY(root):
In MIN-HEAPIFY(root), it is assumed that the sub-trees, which
are rooted at the child of the root, are min-heaps and it takes a
time complexity of 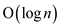 to heapifies
the tree.
to heapifies
the tree.
Now consider the following 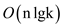 -time
algorithm to merge
-time
algorithm to merge 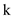 sorted lists
into one sorted list.
sorted lists
into one sorted list.
Algorithm:
1. Build a min-heap by choosing the first element from each of
the  sorted
lists. The heap size is
sorted
lists. The heap size is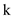 , so
BUILD-MIN-HEAP will take
, so
BUILD-MIN-HEAP will take 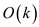 time to
build the min-heap. In this heap, list-id of the list (or from
which list it has been taken) will also be stored along with the
heap elements.
time to
build the min-heap. In this heap, list-id of the list (or from
which list it has been taken) will also be stored along with the
heap elements.
At this stage, the root contains the minimum of the min-heap.
2. Now, put the root into the final sorted list. Then, the root
will be replaced with the next elements of the same list. It will
take a time complexity of 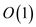 time.
time.
At this stage, the min-heap property may be violated by the root.
3. Now, run the MIN-HEAPIFY(root). The time taken in this
is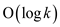 .
.
4. When the list is empty then repeat step (2) for non-empty list.
Running time analysis of the above algorithm:
In the above algorithm, step (1) will take a time complexity of
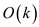 by
the BUILD-MIN-HEAP.
by
the BUILD-MIN-HEAP.
The step (2) and step (3) will be repeated  times. So,
the total time complexity can be calculated by multiplying
complexity of both steps by n.
times. So,
the total time complexity can be calculated by multiplying
complexity of both steps by n.
Calculate the total running time as follows:
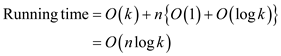
Hence, the running time of the algorithm is 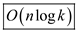 .
.