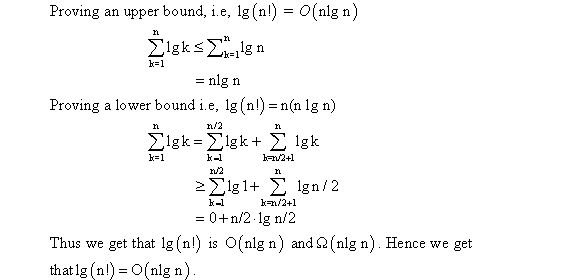The smallest possible depth of a leaf in a decision tree for a sorting algorithm is 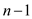. This is because the minimum number of comparisons that are necessary to sort an array of size n is .

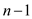Consider the decision tree for insertion of sort operation for three elements given in the figure 8.1 in the textbook.

Consider an array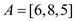. From the figure 8.1, it is clear that in order to check whether the array A is sorted or not, it is necessary to compare the nodes (1:2), (2:3), and (1:3).

Hence, the number of comparisons that are necessary to sort an array of size 3 is 3.

Consider an array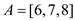. The array is already in a sorted order. From the figure 8.1, it is clear that in order to check whether the array A is sorted or not, it is necessary to compare the nodes (1:2) and (2:3).

Hence, the number of comparisons that are necessary to sort an array of size 3 is 2 which is equal to.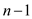

Hence, the minimum number of comparisons that are necessary to sort an array of size n is .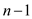

For at least half of the n! Inputs of length n:

Assume a decision tree T which have the height h with the reachable leaves r corresponding to the comparison sort of the n elements.

Theorem 8.1 proof that any comparison sort algorithm need 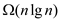time in worst case.

From this theorem, the equation can be write as .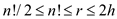

Now by taking the logarithms of this equation, it can be write as:

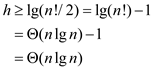
Hence, from the above result, it is concluded that there is no comparison sort whose running time is linear for the at least half of the n! Inputs of n length.

Fraction of 1/n of the inputs of length n:

Assume a decision tree T which have the height h with the reachable leaves r corresponding to the comparison sort of the n elements.

Theorem 8.1 proof that any comparison sort algorithm need 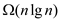time in worst case. From this theorem, the equation can be write as .

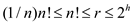Now by taking the logarithms of this equation, it can be write as:

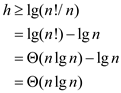
Hence, from the above result, it is concluded that there is no comparison sort whose running time is linear for Fraction of 1/n of the inputs of length n.

Fraction of 1/2 ⁿ of the inputs of length n:

Assume a decision tree T which have the height h with the reachable leaves r corresponding to the comparison sort of the n elements.

Theorem 8.1 proof that any comparison sort algorithm need 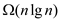time in worst case. From this theorem, the equation can be write as .

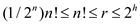Now by taking the logarithms of this equation, it can be write as:

Hence, from the above result, it is concluded that there is no comparison sort whose running time is linear for Fraction of 1/2ⁿ of the inputs of length n.

Suppose that A be the sequence which is having the n number of elements. This sequence is divided into the subsequence of length k that is n/k for each of length k and in any subsequence, all the elements are greater than the all elements of the earlier subsequence. In any subsequence, all the elements are smaller than the all of the elements of the subsequent subsequence.

Now to show that 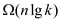is the lower bound on the comparison, it is needed to solve the specified variant of sorting problem.

• First of all consider a decision tree of given height h for the comparison sort for sequence A. As the elements of the every subsequence may be in any order, therefore any of the k! Correspond to the last and final sorted order of the subsequence.

• As there are the n/k subsequence, so each of that may in any order and there are the total permutation of A which can be crossponding to sorting of some input order. Hence, for sorting of sequence A, any decision tree must have the number of leaves at least.

• Any binary tree with the height of h does not have more than 2^h leaves, so it can be concluded that 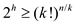or by taking the logarithms, and it can be write as:.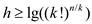

• Now the equation 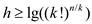can be solved further to get the result as:

• Now, it can solved or write as 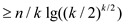because k! is having the k/2 as its largest terms being at least for k/2 each (refer exercise 8.1.2 solution).

This equation can be further solve as:

Thus, lower bound on the number of comparisons needed to solve the specified variant for sorting problem is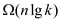.