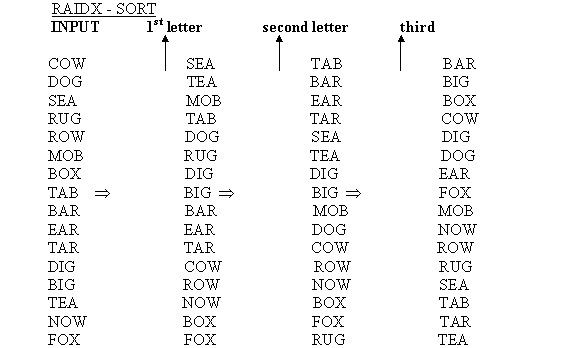
Radix sort is the most common linear sorting algorithm for the integers. Radix sort sorts based on the digits in the given input numbers.

• This algorithm is mostly used by the card sorting machines.

• Radix sort solve the card sorting problem by sorting on least significant digit first. Then sorting on the second least significant digit and so on.

• For the correct working of radix sort, digit sorts must be stable.

Consider an array of n-numbers where each number consist d digits, such that digit 1 is the least significant digit and digit d is the most significant digit.

Refer to the section 8.3 for the RADIX-SORT algorithm.

Proving working of Radix Sort using Induction:

Base step:

• Assume that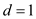. That is, there is only single digit in the given numbers.

• Then radix sort sorts the array on that single digit.

• That is, if d=1, radix sort performs sort on one column and gives the sorted array.

• Therefore, radix sort works for single digit numbers.

Induction step:

• Assume that the radix sort works well on 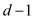digits or 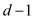columns.

• Now, it is enough to prove that radix sort can also works for d digits.

• Since Radix sort works separately on each digit, starting from the least significant digit(digit 1) to most significant digit(digit d) and by induction hypothesis, before sorting on digit d, radix sort sorts well on lower-order d-1 digits.

• That is, after sorting on digit d-1, the numbers are ordered according to their low-order d-1 digits.

• Now the sort is performed on digit d and it orders the numbers based on their dth digit as follows.

• Sort on dth digit:

Consider the two numbers x and y, such that and are the dth digits of x and y respectively.

• If then the number x is placed after y in the array, irrespective of the lower-order d-1 digits.

• If then the number x is placed before y in the array, irrespective of the lower-order d-1 digits.

• If then the numbers x and y are left in their original order in the array, because it is assumed that the intermediate sort is stable. Since dth digits are equal and the order of x and y are not changing, the correct order of x and y is determined by the lower-order 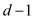digits.

In the proof, the assumption that the intermediate sort is stable is required when sorting numbers on their dth digit and whose dth digits were equal.

• Since the dth digits were equal, the correct order of numbers is already determined after sorting by their lower-order d-1 digits.

• If the intermediate sort was not stable, the numbers correctly ordered by sorting on their lower ordered d-1 digits are rearranged while sorting on dth digit.

Therefore the given assumption is required when sorting numbers on their d th digit and whose d th digits were equal.

Treat the numbers as 3 - digit numbers in radix n. Each digit ranges from 0 to n-1. Sort these 3 – digit numbers with radix sort.

These are 3 calls to counting sort, each taking 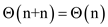time

Therefore, the total time is.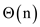

Sort the numbers on the most significant digit, sort each of the resulting bins recursively and combine the decks in order. Therefore, the cards in 9 out of 10 bins are put aside to sort each of the bins. In this way, the intermediate piles of card are generated. The entire deck is sorted again on the second lest significant digit and recombined. The cards are sorted on all d-digits, so cards are fully sorted on the d-digit number. Therefore, only d passes are required to sort d-digit decimal numbers in worst case.

If the decimal number is of d -digit, then for decimal digits, only 10 places are used in each column. A field of d columns is occupied by a d-digit number. The number of bins in each column are 10 and it is required that a single pass must sort each bin.

Therefore, 10d passes are required to sort d-digit decimal numbers in worst case.

Suppose the cards in 9 of the 10 bins must be put aside to sort each of the bins. This procedure generates many intermediate piles of cards that must be kept track of. Accordingly, whenever 1 bin in one column is sorted, keep track of rest 9 bins in each column. For each 10d bin, keep track of 9 bins so that we need to keep track of 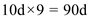piles of cards. Therefore, in the worst case, an operator would need to track 90d piles of cards.