Compare the elements in a tournament fashion by splitting the elements in pairs and comparing each pair and then proceeding to compare the winners. In this way, the problem is reduced to size 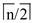and only one element is left in the end.

There will be n-1 matches and one winner will be selected and second smallest element is one of the lgn elements and this element is lost to the smallest such that it is smaller than the ones it has been compared to. Thus, 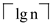– 1 comparisons can be used to find the smallest element.

The total number of comparisons are .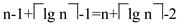

Optimal number of comparisons required to find the maximum and minimum of n numbers in the worst-case scenario:

Step 1: Set initial values for the minimum and maximum.

i. If n is odd, minimum and maximum are set to the value of the first element.

ii. If n is even, compare the first 2 elements and assign the smaller element to minimum and larger element to maximum.

Step 2: Process elements in pairs.

i. Compare pairs of elements from the input with each other.

ii. Compare the smaller to the current minimum.

iii. Compare the larger to the current maximum.

The processing of elements is done in pairs. Therefore , 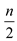pairs are processed.

To process each pair of elements, 3 comparisons are required as described in step 2.

Hence, 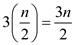comparisons are required.

If n is odd, 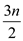comparisons are performed.

If n is even, one initial comparison is done to set initial value for maximum and minimum and 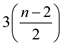comparison are performed for the remaining 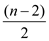pairs.

Thus, the total number of comparisons performed when n is even can be known by adding 1 to 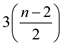as shown below:

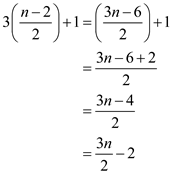
Hence, number of comparisons when n is odd is 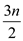and number of comparisons when n is even is.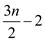

In the worst case scenario, consider the upper bound to calculate the total number of comparisons.

Hence, 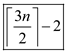comparisons are necessary to find both the minimum and the maximum of n numbers.