a)

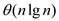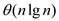Using Merge sort or Heapsort the sorting can be done in time. Here, is the worst-case time. Do not use quicksort or insertion sort as it takes worst case time of . Put the i largest elements into the output array taking 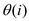time.

Total worst case running time: =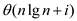

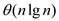
b)

Implement the priority queue as a heap. Build the heap using BUILD-HEAP which takes 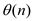time then call HEAP-EXTRACT MAX, i times to get the i largest elements in 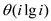time and store them in reverse order of extraction in the output array.

So, total running time:

c)

Use SELECT algorithm to find the 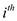largest number in 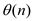time. Call partition that takes 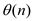time. Sort the i largest numbers in 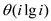worst case time (with merge-sort or heap sort).

Total worst case running time:

Median

A median is a half way point of the set. When there are n elements and n is an odd number then median is:

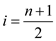, where 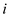^th element is the median

When n is an even number, then median point is:

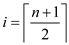OR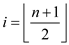

(Upper bound) OR (Lower bound)

Weighted median: Weighted median is stated as arithmetic mean of all observable samples and is represented with the help of formula:

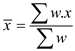
Where w is the sample weight.

a .

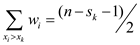Let be the number of elements which are smaller than . When the weights of 1/n are assigned to each , then the summation and . This sum is <1/2 and 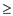1/2 respectively when 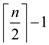and it is made by value of . The value of x must be the median because it has equal numbers of ’s that are smaller and larger than it

b .

To point out the weighted median of n elements in worst time running of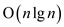, sort the items using merge-sort or heap-sort whose complexity is 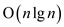. For this, starting with the first item iterate over the items in first list, taking the sum of the weights of the items at the time of execution, until the running sum does not go over 0.5. Thus, on going with the algorithm as:

Sort-Weighted- Median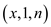

// applying any of the merge sort or heap sort on the items.

1. Merge so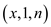rt or heap sort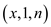

// initializing the value of variable sum

2.

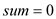
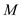// - number of the present element

3.

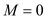
// iterate the loop until the less than 0.5

4. while ()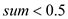

// increasing the value of M by one.

5.

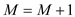
// adding the 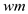- weight of the element in the sum

6.

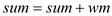
// end of while loop.

7. end while

8. return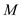

Analysis of algorithm:

The analysis of the above algorithm for the calculation of complexity is as:

Step 1 has complexity of 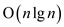as it the complexity of merge sort and heap sort.

Step 2 and step 3 are of 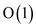since, they are simple assignments.

Steps 4, 5, 6 are of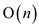 , since loops for n items.

Thus, on calculating the complexity:

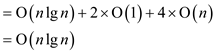
Hence, Proved.

c .

Modify SELECT so that time is linear. Let x be the median of the medians. Check which one of 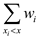and 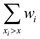is larger than ½. Perform recursion on the collection of smaller or larger elements which contain weighted median. The runtime is .

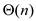d .

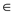Let the minimizer be p and suppose p is not weighted median. Let be the quantity which is very small such that where k is not included if 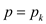. If the weighted median is denoted by and 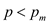, then choose a quantity 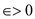otherwise it can be said that 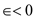. Since, p is chosen to minimize the cost so, the expression can be computed as follows:

which is equal to

The difference in sum will take opposite sign.

e .

Since,

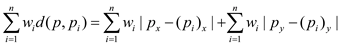
Each sum is minimized which can be done as and 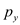is to be chosen separately. Thus, take such that is the weighted median of the x-coordinates of and the weighted median of the y-coordinates of the is denoted by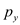

Consider the SELECT algorithm provided in section. This algorithm is used to find very efficiently the i^th smallest element in any unsorted Arr[ ].

When value of i is very small that is the finding element is very small as compare to the number of elements in an array. At this time SELECT algorithm gets inefficient, it is because due to avoiding unnecessary comparison.

a.

Consider the following MODIFIED-SELECT algorithm to determine ith smallest element in the array of n number of elements.

FIND(Arr ,i ,n)

1. if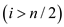

2. SELECT(Arr , i, n)

3. else

4. MODIFIED-SELECT(Arr,i,n)

MODIFIED-SELECT (Arr, i , n)

1.

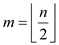
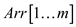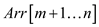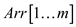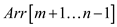2. When n is even then divide array Arr in two parts that is and . When n is odd then divide array Arr in three parts that is, and.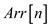

3. for 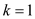to m

4. if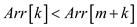

5. SWAP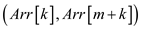

6. Recursively called the MODIFIED-SELECT algorithm in 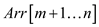to find ith smallest element. After this the i^th smallest element of 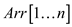must be eithe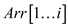r or.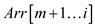

7. Now, at last collect 2i elements from 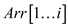and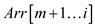, and put it in another array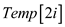. Now call SELECT function to determine i^th smallest element.

Comparison:

• In the first two lines of above algorithm, the array will be partitioned into two parts.

• The line 3-5, performs m comparisons, where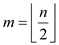

• The 6^th line recursively call itself with elements of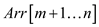, therefore the number of comparisons are .

• The last step call the SELECT function with 2i elements, therefore the number of comparisons are.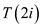

• Hence, the numbers of comparisons in MODIFIED-SELECT are.

b.

According to above stated part (a), if 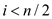, the numbers of comparison in MODIFIED-SELECT are:

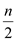Put value recursively in by replacing with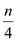

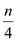Put in the above equation by replacing with

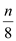
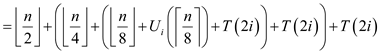
Do this recursively k times.

Then can be written as,

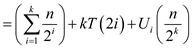…… (1)

From the definition of ith smallest element, the comparisons stop when the size of the array partition is equal to i. That is, when the size of the partition () is equal to i.

Therefore,

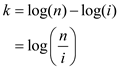
Put this value in equation (1),

From the geometric sum, 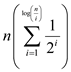will be almost n and replace n in the above equation.

Then

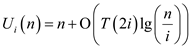
Hence, proved that is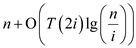

c.

When value of i is constant then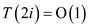, also

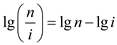
As value of i is constant therefore 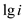is constant

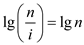
Now, put the above values in equation (1), therefore

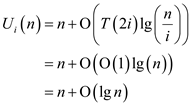
Hence, proved that is 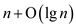when i is constant.

d.

Consider the equation (1) when.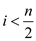

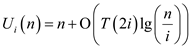
Here, 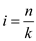where

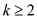
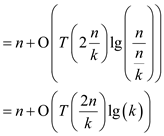
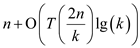Hence, proved that is when .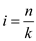

Alternative analysis of randomized selection

a. In quick sort two elements and will be compared if they lie in the same partition. In other sense it can be said that two elements and will not be compared if they lie in separate partitions. That is two elements and will not be compared if a pivot element is chosen from the set.

Now, consider that 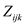is defined as below,

It is quite obvious to see that until the pivot element is from set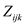, each and every element of 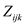will be in the same partition and any element of the 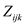will have same probability to be selected as the pivot.

So,

Probability { or is the first pivot chosen from}

= Probability { is the first pivot chosen from}

+ Probability {is the first pivot chosen from}

=

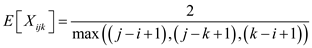… … (1)

b. Consider that denote sum of the comparisons between elements of array 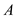when finding.

Total number of comparisons that is can be given by following summation,

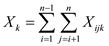
By linearity of expectation,

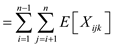
Substituting the value of from equation (1) results in,

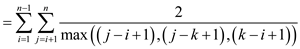
In order to solve the 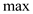function its needed to divide the summation condition in such a way as in that range there will be only one maximum out of the three.

That is; the sum could be break in three cases:

1.

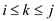
2.

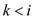
3.

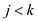
Breaking as above the result will be,

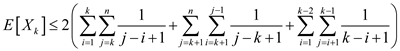
Further simplifying it results in,

Hence,

… … (2)

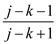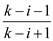c. Since, is a fraction that is strictly less than 1. Same way is a fraction strictly less than 1.

Therefore,

is summation of the fraction less than 1 for 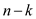times … … (3)

is summation of the fraction less than 1 for 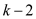times … … (4)

Form (3) and (4),

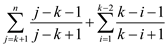Will always be less than … … (5)

Now, consider the first part of summation from equation (2),

Assume that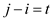. It is obvious to get that there can be at max 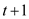ways for 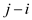to be.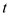

Therefore it can be rewritten as

… … (6)

From (5) and (6),

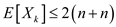
Hence Proved.

d. To prove the following, assuming all elements of array A are distinct, RANDOMIZED-SELECT executes in the assumed time.

Proof:

In order to prove that RANDOMIZED-SELECT executes in primarily assumed time, there is need to apply the Lemma 7.1 for RANDOMIZED-SELECT. To do this replace the variable X in the Lemma 7.1(Refer PAGE 182) by the randomly selected variable as mentioned above.

There fore, the total execution time of RANDOMIZED-SELECT as expected is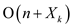which can be represented as.

Hence, the running time of the RANDOMIZED-SELECT is for the distinct elements of array A.